Основы динамики нагрева

Основой для теплового расчета нагревательных устройств является совместное решение уравнений теплового баланса и теплопроводности с учетом динамики нагрева.

Процессы нагрева связаны с изменением теплосодержания нагреваемых материалов, явлениями теплопередачи и по своей природе являются динамическими.

Для простоты рассмотрим случай нагрева однородного и изотропного тела, обладающего бесконечной теплопроводно­стью и неизменностью физических параметров тела, кроме тем­пературы /.

В этом случае уравнение теплового баланса за время dx имеет вид

dQ_±=dQ₂+dQ_3y (2.29)

(2.31)

(2.32)

где dQ\ — количество тепла, подводимого к телу за время dx, Дж; dQ₂ — количество тепла, идущее на изменение теплосодер­жания тела; dQz — потери тепла в окружающую среду, Дж.

Составляющие теплового баланса (2.29) определяются вы­ражениями:

dQ^P-dx,

где Р — мощность, подводимая к телу, Вт;

dQ₂ - Mcdt,

где М — масса тела, кг; с — средняя удельная теплоемкость те­ла за период нагрева, Дж/кг°С; dt — изменение температуры тела за время dx, °C;

dQ₃^kF(t-t₀,_c)dx_y

где k — коэффициент теплопередачи от нагреваемого тела в ок­ружающую среду, Вт/м²°С; F — поверхность теплопередачи, м²; to._u — температура окружающей среды, °С. В итоге уравнение (2.29) принимает вид

Pdx=Mcdt + kF{t—t₀._c)dx (2.30)

Мс kF

или

+ t-

to.c +

kF

dt ' dx

Мс kF

Tut,

o.c f-TT-^y» уравнение (2.31) мож- kF

Обозначив

dt

но записать в виде

dx

-t—t_y = 0₉

где Т —постоянная времени нагрева, с; f_y — установившаяся температура тела [при-—=0).

Решением дифференциального уравнения первого порядка будет следующее выражение:

t*=t_Be-*'^T + t_J(l—*-'"^T) (2.33)

где t_H — начальная температура тела при т=0.

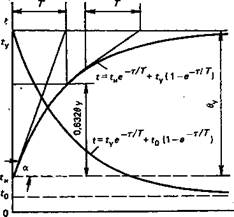
Выражение (2.33) не что иное, как уравнение нагрева од­нородного тела, позволяющее найти текущее значение темпера­туры в любой момент времени т. Графически это экспонента (рис. 2.8), начинающаяся с t = t_H при т=0 и при т-^оо ассимп-тотически приближающаяся к установившемуся значению t_y.

Установившийся режим наступает практически при

^=(34-4) Г, а значение t для этого момента примерно равно /^(0,95-0,98)/_у.

Из уравнения (2.33) легко получить выражение для опре­деления времени нагрева тела до температуры t в промежутке от t_H до t_y:

*v—/_n

(2.34)

т-Пп Л

t_Y—t

(2.35)

Уравнение (2.33) можно представить в виде # = #_н е-т/г + #_у (1 _ *-*/*),

где Ф=/—^о.с; $H=t_H —/o.c и fty^ty — t₀.c — соответ­ственно текущее, началь­ное и установившееся превышение температуры тела над окружающей средой.

Мс

Постоянная времени

является

нагрева Т = -£р

Рис. 2.8. Кривые нагрева и охлаж­дения однородного тела

важным параметром теп­лового объекта и означа­ет время, в течение кото­рого тело достигло бы установившейся темпера­туры без теплоотдачи в окружающую среду (ади­абатический нагрев). В этом случае А=0и выра­жение (2.30) представля­ло бы собой уравнение прямой линии,. На этом

При х—Т по

основано графическое определение величины Т. уравнению (2.35) находим, что Ф = 0,632 Ф_у.

Положив в уравнении (2.30) Р = 0, получим уравнение ох­лаждения

* = *_у е~*'^т +1₀ (1 — е-^гг). (2.36)

или по аналогии с (2.35):

0=О_у£Г"^т/г. (2.37)

где Т —постоянная времени охлаждения, которая может быть и неравной постоянной времени нагрева.

Кривые нагрева реальных объектов безусловно отличаются от приведенных на рис. 2.8 в связи с принятыми упрощениями

при выводе уравнения (2.33). Но при этом общий принцип ди­намики нагрева и характеризующие его параметры остаются неизменными. Процессы нагрева реальных объектов описывают­ся уравнениями более высоких порядков и не всегда решаются простыми способами.

-г/Т

В тепловом процессе важной характеристикой является скорость нагрева. Продифференцировав уравнение (2.33) по т, получим

е

М, _ h —^н р—х/т₌₌ * —*н

е-т/г^ _iz2H_._2----------- ----------- (2.38)

dx T T i___e-r/r '

Из формулы (2.38) следует, что при данной мощности, под­водимой к телу, скорость нагрева снижается по мере возраста­ния температуры тела. В начальный момент т=0 скорость на­грева наибольшая:

(JL). \ dx;%=o

IrzhL. (2.39)

При расчете и проектировании ЭНУ иногда приходится ог­раничивать скорость нагрева, так как это отрицательно сказы­вается на физико-химических свойствах нагреваемых материа­лов, что ухудшает качественные показатели обрабатываемых изделий.

Дата добавления: 2015-04-24