Сравнение. Методы сравнения статистических совокупностей

Методы сравнения статистических совокупностей.

Виды распределений.

Нормальное (Гауссово, симметричное, колоколообразное) распределение – одно из самых важных распределений в статистике. Оно характеризуется тем, что наибольшее число наблюдений имеет значение, близкое к среднему, и чем больше значения отличаются от среднего, тем меньше таких наблюдений. Примерами характеристик, подчиняющихся нормальному распределению, являются показатели роста, веса, какие-либо биохимические показатели крови.

Гауссово распределение характеризует распределение непрерывных случайных величин и встречается в природе наиболее часто, за что и получило название «нормального».

Кривая нормального распределения имеет следующие свойства:

· колоколообразна (унимодальна);

· симметрична относительно среднего;

Среднее арифметическое, мода и медиана при нормальном распределении равны и соответствуют вершине распределения:

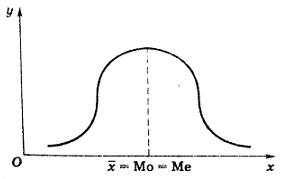
От вида распределения (нормальное или нет) и типа исследуемого признака (данные количественные или качественные) зависит выбор подходящего критерия сравнения. Критерии делятся на два типа – параметрические (критерии Стьюдента, Фишера, Пирсона) и непараметрические (критерии Манна-Уитни, Вилкоксона, z-критерий). Параметрические критерии применяются только в случае нормального распределения данных. Если распределение отличается от нормального, то следует пользоваться непараметрическими критериями.

Если признаки количественные (выражены численно), то для сравнения данных применяются критерий Стьюдента, Манна-Уитни или Вилкоксона.

Если признаки качественные (характеризуют свойство), то для сравнения данных применяются критерий хи-квадрат (критерий Пирсона) или Z-критерий.

Дата добавления: 2015-04-24