
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 2. Оптимальный доход равен:
|
|
|
|
Й шаг.
Й шаг.
Й шаг.
Й шаг.
Оптимальный доход равен:
z *4(a 4 )= 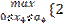 a 4+ x 4}= 3 a 4,
a 4+ x 4}= 3 a 4,
т.к. линейная возрастающая функция достигает максимума в конце рассматриваемого промежутка, т.е. при x 4= a 4.
z *3(a 3)=  a 3+ x 3 + 3(0,5 a 3– 0,4 x 3)}=
a 3+ x 3 + 3(0,5 a 3– 0,4 x 3)}= 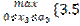 a 3– 0,2 x 3)}=
a 3– 0,2 x 3)}= 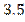 a 3
a 3
т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при x 3= 0.
z *2(a 2)= 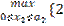 a 2+ x 2 + 3.5(0,5 a 2– 0,4 x 2)}=
a 2+ x 2 + 3.5(0,5 a 2– 0,4 x 2)}=  a 2– 0,4 x 2)}=
a 2– 0,4 x 2)}=  a 2,
a 2,
т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при x 2=0.
z *1(a 1)=  a 1+ x 1 + 3.75(0,5 a 1– 0,4 x 1)}=
a 1+ x 1 + 3.75(0,5 a 1– 0,4 x 1)}= 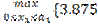 a 1– 0,5 x 1)}=
a 1– 0,5 x 1)}= 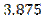 a 1,
a 1,
т.к. линейная убывающая функция достигает максимума в начале рассматриваемого промежутка, т.е. при x 1=0.
Результаты оптимизации:
z *1(a 1)= 3,875 a 1, x *1 =0,
z *2(a 1)= 3,75 a 2, x *2 =0,
z *3(a 3)= 3,5 a 3, x *3 =0,
z *4(a 4)= 3 a 4, x *4 = a 4.
Определим количественное распределение средств по годам:
Т.к. a 1= a =1000, x *1=0, получаем a 2=0.5 a 1– 0.41 x *1=500. Далее аналогично:
x *2=0, a 3= 0.5 a 2–0.4 x *2=250,
x *3=0, a 4= 0.5 a 3−0.4 x *3=125,
x *4= a 4=125.
Представим распределение средств в виде таблицы:
| предприятие | год | |||
При таком распределении средств за 4 года будет получен доход, равный
z *1(a 1)= 3,875 ·1000= 3875.
Строительный подрядчик оценивает минимальные потребности в рабочей силе на каждую из последующих пяти недель следующим образом, 6, 5, 3, 6, 8 рабочих соответственно. Содержание избытка рабочей силы обходится подрядчику в 300 долларов за одного рабочего в неделю. А наем рабочей силы на протяжении одной недели обходится 400 долларов плюс 200 долларов за одного рабочего в неделю. Каждому уволенному рабочему выплачивается выходное пособие в размере 100 долларов. Найти оптимальное решение задачи.
Решение.
1. Этап i представляется порядковым номером недели, i = 1, 2, 3, 4, 5.
2. Вариантом решения на i -том этапе являются значения 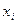 –количество работающих на протяжении i -той недели.
–количество работающих на протяжении i -той недели.
3. Состояние на i -том этапе является 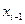 – количество работающих на протяжении (i- 1)-й неделе.
– количество работающих на протяжении (i- 1)-й неделе.
Рекуррентное уравнение динамического программирования представляется в виде:
 – затраты, связанные с содержанием избытка;
– затраты, связанные с содержанием избытка;
 – затраты, связанные с наймом;
– затраты, связанные с наймом;
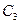 – затраты, связанные с увольнением.
– затраты, связанные с увольнением.
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Проведем оптимизацию, начиная с пятого этапа:
Этап 5.

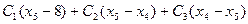 Оптимальное решение Оптимальное решение
| |||

| 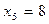
|  
| 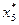
|
| 300*0+400+200*2+100*(-2)= 600 | |||
| 300*0+400+200*1+100*(-1)= 500 | |||
| 300*0+400+200*0+100*0= 400 |
Этап 4.

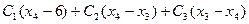 + +  Оптимальное решение Оптимальное решение
| |||||
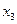
|  = 6 = 6 
|  = 7 = 7
|  = 8 = 8
|  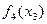
| 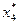
|
Этап 3.

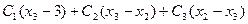 + + 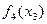 Оптимальное решение Оптимальное решение
| ||||||

| 
| 
| 
| 
| 
| 
|
Этап 2.

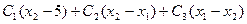 +
+  Оптимальное решение
Оптимальное решение

|  = 5 = 5 
| 
| 
|
| 300*0+400+200*(-1)+100+1500=1800 | |||
| 300*0+400+200*(-2)+200+1500=1700 | |||
| 300*0+400+200*(-3)+300+1500=1600 |
Этап 1.
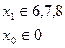
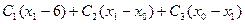 +
+  Оптимальное решение
Оптимальное решение
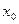
|  = 6 = 6
|  = 7 = 7
|  = 8 = 8
|  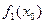
| 
|
Оптимальное решение определятся последовательно таким образом:
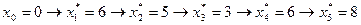
| Номер недели | Минимум раб.силы | Кол-во реально работающих | Решение |
| Нанять 6 рабочих | |||
| Уволить 1 рабочего | |||
| Уволить 2 рабочих | |||
| Нанять 3 рабочих | |||
| Нанять 2 рабочих |
Вывод: в результате решения задачи получилось, что на первой неделе надо нанять 6 человек, на второй уволить 1 рабочего, на третьей уволить 2 рабочих, на четвертой нанять троих рабочих и на пятой нанять двоих рабочих.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 758; Нарушение авторских прав?; Мы поможем в написании вашей работы!