Анализ структурного графика (графика частот вращения)

Построение структурного графика (графика частот вращения)

График частот вращения (структурный график) (рис. 4) является видоизмененной струк­турной сеткой. Он показывает действительные значения част­ных передаточных отношений передач и частот вращения валов.

Для построения графика частот вращения необходимо рассчитать числа оборотов шпинделя по формуле

n_i = n _min × j ^i-1

Для нашего примера при j = 1,26

n₁ = n_min = 160 об\мин n₄ = n_min × j³ = 320,07 об\мин

n₂ = n_min × j¹ = 201,6 об\мин n₅ = n_min × j⁴ = 403,3 об\мин

n₃ = n_min × j² = 254,4 об\мин n₆ = n_min × j⁵ = 508,1 об\мин

Принимаем в соответствии с нормальными рядами чисел в станкостроении (см. Приложение 3) следующие значения чисел оборотов шпинделя:

n₁ = n_min = 160 об\мин n₄ = n_min × j³ = 315 об\мин

n₂ = n_min × j¹ = 200 об\мин n₅ = n_min × j⁴ = 400 об\мин

n₃ = n_min × j² = 250 об\мин n₆ = n_min × j⁵ = 500 об\мин

Выполните анализ по отклонению D n % £ ± 10 (j-1)

В нашем примере D n % £ ± 10 (1,26-1) = 2,6 %

Сравнивая расчетные и стандартные значения частот вращения шпинделя, можно увидеть, что наибольшая разность соответствующих частот вращения имеет место для верхней ступени и составляет 1,62 % что меньше допускаемого отклонения.

3.4.1 Последовательность построения сетки для структурного графика (графика частот вращения) (Рис. 4) аналогична последовательности построения структурной сетки. Точка, соответствующая частоте вращения первого вала выбирается максимально высокой. При совпадении частоты вращения первого вала с частотой вращения двигателя количество валов (количество вертикальных линий) не меняется. При частоте вращения первого вала большей или меньшей частоты вращения двигателя, график дополняется валом двигателя – вертикальной линией слева от первого вала с номером 0. Для изменения (понижения) частоты вращения первого вала по отношению к частоте вращения двигателя используют ременную или зубчатую передачу между валами 0 и 1.

3.4.2 Точка 1 должна занимать положение на вертикальной линии положение, приближенное к n max. Наклонные линии основной коробки расходятся на величину одного интервала. Для других коробок наклонные линии расходятся на величину интервала, соответствующего выбранной характеристике.

3.4.3 Количество линий с разными наклонами соответствует числу скоростей проектируемой ступени.

Лучи с наклоном вверх (считая слева направо) изобра­жают ускорительную передачу (i>1), а направленные вниз - эамедляющую передачу (i<1), горизонтально расположенные линии соответствуют передаточному отношению i=1

Передачи с наибольшим уменьшением называют базовыми передачами коробок скоростей: Z1: Z2 и Z7: Z8.

Анализ графика частот вращения производится по показателям:

3.5.1 Частоту вращения первичного вала желательно выбирать наибольшей. В общем случае частоту вращения приводного вала целесообразно принимать n = n _мах где n _мах – верхний предел регулирования, В нашем случаеданное условие соблюдается

n = n _мах = 500 об\мин

Так как электродвигатели имеют большие частоты вращения (табл. 5), то предполагается использовать зубчатую или ременную передачу между валами 0 и 1

3.5.2 Передаточное отношение в группах должно посте­пенно уменьшаться по мере приближения к шпинделю.

3.5.3 Для ограничения размеров зубчатых колес и радиаль­ных габаритов коробок скоростей нормалями станкостроения установлены пределы передаточных отношений:

i min ³ 1/4, I max £ 2

Передаточные отношения, удовлетворяющие этому условию возможны в том случае, если число полей между линиями, условно обозначающими передачи, при выбранном j не превышает указанное в табл. 3.

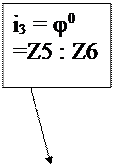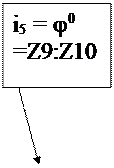1 2 3

i₁ = 1\j² =Z1: Z2

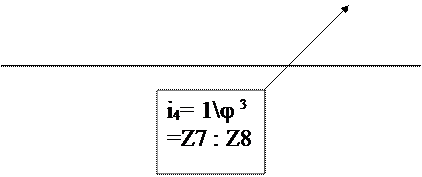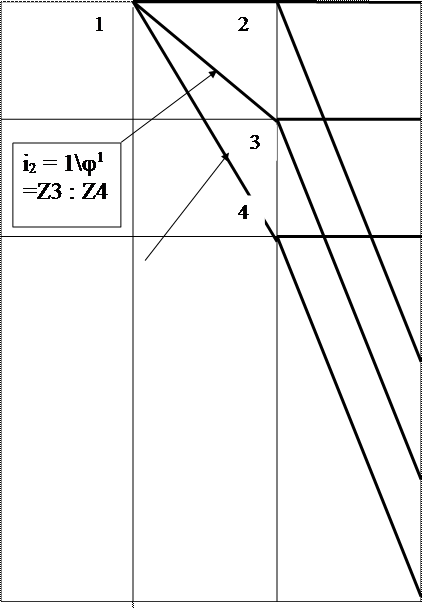
Рис. 4. Структурный график или график частот вращения для коробки Z=6 = 3₁ ´ 2₃

Таблица 3

Максимальное число полей, допускаемое для пересечения линиями передач на структурном графике

Передачи	Число интервалов (показатель степени j)
j = 1,12	j = 1,26	j = 1,41	j = 1,58	j = 1,76
Понижающая
Повышающая

Для Z = 6= 3₁ × 2₃ и j = 1,26

i_наиб = j⁰ = 1,26⁰ = 1 i_наим = j^-3 = 1,26^-3 = 1\2, (см. табл. 4)

В рассматриваемом случае соблюдаются оба условия, следовательно данная структура может быть применена.

Рассмотрим в качестве примера сложную коробку скоростей с числом ступеней Z = 12 и j = 1,26, n_min = 63 об/мин

Структурная формула такой коробки запишется в виде

Z = 3₁ ´ 2₃ ´ 2₆

Построим для этой коробки структурную сетку и проведем её анализ с точки зрения соблюдения условий, рассмотренных в разделе 3.3. Кинематическая схема и структурный график приведены на рис. 5 и

рис. 6

1. Симметричность и веерообразность расположения лучей.

Структурная сетка симметрична в пределах каждой группы.

2. Соблюдение вышеперечисленных условий выбора оптимального варианта компоновки коробки скоростей. Число передач основной группы равно 3 и соответственно уменьшается по мере приближения к шпинделю Z₂ = 2, Z₃ = 2. Кинематические характеристики групп увеличиваются по мере приближения к шпинделю х₀ = 1, х₁ = 3, х₂ = 6.

3. Проверка выбранного варианта сетки по диапазоны регулирования.

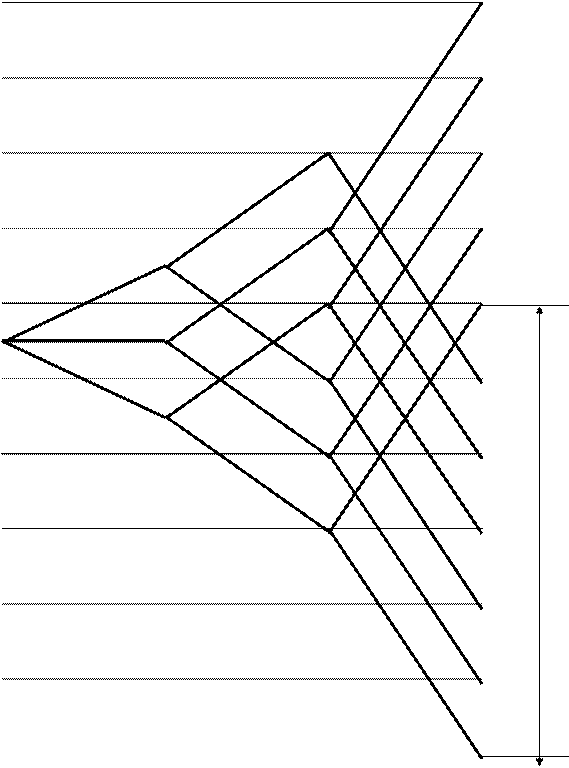
Условие оптимальности R £ [R], где [R] = 8

Структурный график (график частот вращения) для данной коробки скоростей приведен на рис. 7, на основании которого

В примере R = 1,26 ^6(2-1) = 4< [R] = 8

i_min =j ^-6= 1,26 ^-6 = ¼; i_max =j ⁰= 1

Все условия соблюдены, следовательно рассматриваемый вариант структуры можно считать оптимальным.

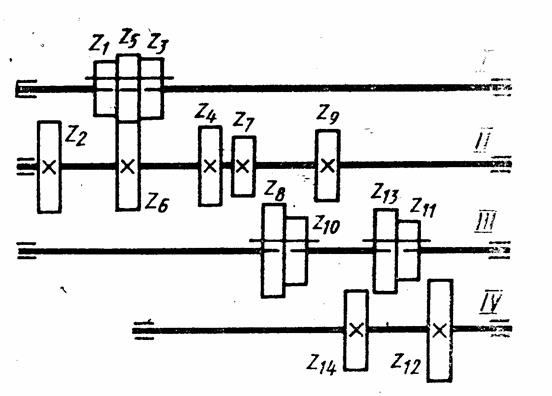
Рис.5. Кинематическая схема коробки скоростей Z = 12 = 3₁ ´ 2₃ ´ 2₆

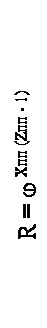
Х = 1 Х = 3 Х = 6

Рис. 6. Структурная сетка для коробки скоростей по формуле

Z = 12 = 3₁ ´ 2₃ ´ 2₆

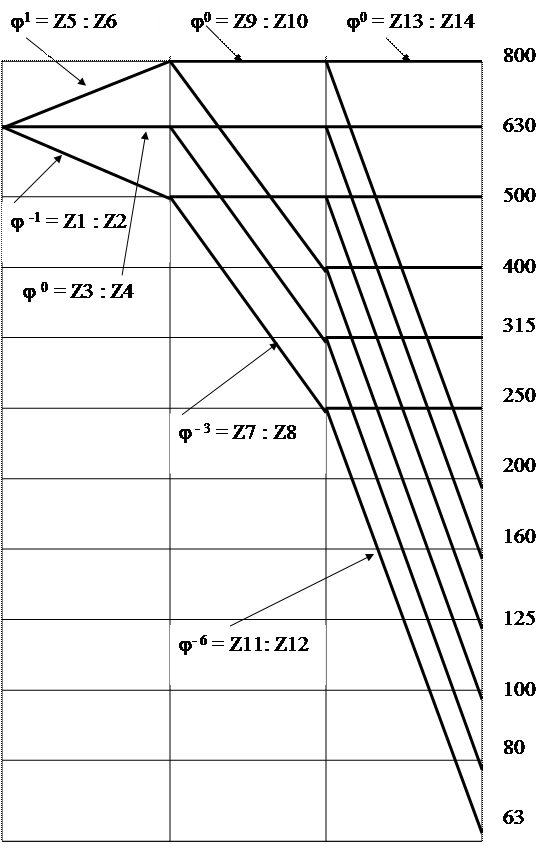Х = 1 Х = 3 Х = 6

Рис. 7. Структурный график для коробки скоростей по формуле

Z = 12 = 3₁ ´ 2₃ ´ 2₆

3.6. Определение передаточных отношений

Частные передаточные отношения определяют по графику частот вращения. Их выражают через знаменатель гео­метрического ряда j:

i = j ^±k

где к - число интервалов между смежными валами, которые пересекает данный луч на графике частот вращения.

Знак «плюс» принимается для ускоряющей передачи, «ми­нус» - для замедляющей передачи, для горизонталь­ных лучей к = 0, i = 1

Передаточные отношения, выраженные через j могут быть представлены в виде простых дробей, которые приведены в табл. 4. Для ускоряющих передач принимаются значения, обратные табличным

j² = 1,26² = 11: 7 j^-2 = 1,26^-2 = 7: 11

Таблица 4

Передаточные отношения для стандартных значений j

(фиктивные числа зубьев)

к	j = 1,26	j = 1,41	j = 1,58
-1	4: 5	5: 7	7: 8
-2	7: 11	1: 2	2: 5
-3	1: 2	19: 53	1: 4
-4	2: 5	1: 4
-5	19: 16
-6	1: 4

По рис. 4, для j = 1,26, в соответствии с таблицей 4:

i₁ = j ^-2 =7: 11 i₄ = j ^-3 = 1: 2

i₂ = j ^-1 = 4:5 i₅ = j ⁰ = 1: 1

i₃ = j ⁰ = 1: 1

3.7. Расчет чисел зубьев

Числа зубьев рассчитывают отдельно для каждой группы передач, используя частные передаточные отношения, найденные по графику частот вращения.

Для зубчатых колес, приводов главного движения, рекомендуется принимать минимальные числа зубьев ведущего колеса 18-20, максимальные для ведомого колеса - 100.

Межосевое расстояние между соседними валами должно быть одинаковым, следовательно:

a_w = (mZ₁ + mZ₂) = const

2

При одинаковом модуле m, в пределах одной группы для обеспечения постоянства межосевого расстояния суммы чисел зубьев сопряженных колес должны быть равными, т.е.

Z₁ + Z₂ = Z₃ + Z₄ = Z₅ + Z₆ = S_Z = const

где Z₁, Z₃, Z₅ - числа зубьев ведущих зубчатых колес элементарной двухваловой передачи; Z₂, Z₄, Z₆ - соответствующие им числа зубьев ведомых зубчатых колес.

Для определения чисел зубьев может быть применен метод наименьшего общего кратного (НОК).

Последовательность расчета чисел зубьев колес коробки скоростей методом НОК.

3.7.1. Определите фиктивные числа зубьев для колес коробки

Для нашего примера для основной группы они определяются исходя из равенства:

A: B = Z₁: Z₂ =j ^-2 = i₁; C: D = Z₃: Z₄ =j ^-1 = i₂;

E: F = Z₅:Z₆ =j ⁰ = i₃.

Для переборной группы исходя из равенства:

G: H = Z₇: Z₈ =j ^-3 = i₄; K: L = Z₉: Z₁₀ =j ⁰ = i₅;

где А, В, C, D, E, F, G, H, K, L – простые целые числа, которые являются фиктивными числами зубьев и выбираются по табл.4.Для основной группы передач получаем:

А = 7, В = 11, C = 4, D = 5, E = 1, F = 1,

Аналогично для переборной группы передач:

G = 1, H = 2, K = 1, L = 1

3.7.2 Определите наименьшее общее кратное Sz

Для определения Sz существует правило: «Sz равно наименьшему общему кратному сумм простых целых чисел для данной группы передач»

Для основной группы передач наименьшее общее кратное сумм

A + B, C + D, E + F = 7 +11, 4 + 5, 1 +, равно Sz = 18

Для переборной группы передач наименьшее общее кратное сумм

G + H, K + L = 1 + 2, 1 +1, равноSz = 6

3.7.3. Вычислите расчетные числа зубьев колес по формулам:

(A + B)

Z₁ = Sz× A

(A + B)

Z₂ = Sz× B

Для основной группы передач:

Z₁ = Sz × A / (A + B) = 18× 7 / (7 + 11) = 7

Z₂ = Sz× B / (A + B) = 18 × 11/ (7 +1 1) = 11

Z₃ = Sz × C / (C + D) = 18× 4 / (4 + 5) = 8

Z₄ = Sz × D / (C + D) = 18 × 5/ (4 + 5) = 10

Z₅ = Sz × E / (E + F) = 18× 1 / (1+ 1) = 9

Z₆ = Sz × F / (E + F) = 18× 1 / (1 + 1)= 9

для первой переборной группы передач:

Z₇ = Sz× G / (G + H) = 6× 1 / (1 + 2) = 2

Z₈ = Sz× H / (G + H) = 6 × 2/ (1 + 2) = 4

Z₉ = Sz× K / (K + L) = 6× 1 / (1 + 1) = 3

Z₁₀ = Sz× L / (K + L) = 6 × 1/ (1 + 1) = 3

3.7.4. Определите действительные числа зубьев колес коробки скоростей

Так как минимальное число зубьев колес должно быть не меньше 18, то рассчитанные числа зубьев умножим на 3 для основной группы и на 10 для переборной группы. Таким образом, после умножения получаем:

Z₁ = 21 Z₇ = 20

Z₂ = 33 Z₈ = 40

Z₃ = 24

Z₄ = 30 Z₉ = 30

Z₅ = 27 Z₁₀ =30

Z₆ = 27

3.7.5 Произведите проверку на равенство сумм чисел зубьев, с целью обеспечения одинакового межосевого расстояния для всех передач в одной группе.

Для основной группы:

Z₁ + Z₂ = Z₃ + Z₄ = Z₅ + Z₆ = 21 + 33= 30 + 24 = 27 + 27 = 54

Для переборной группы:

Z₇ + Z₈ = Z₉ + Z₁₀ = 20 + 40 = 30 +30 = 60

Условие постоянства суммы S_Z соблюдается.

В механизмах с трех- и четырехвенцовыми блоками необходима проверка по условию свободного перемещения блока. Условие гарантирует обеспечение зазора между наружным диаметром соседних колес подвижного блока и наружным диаметром неподвижных колес, над которыми проходит колесо подвижного блока при его переключении.

Для трехвенцового блока (рис. 1в) при зацепленииколес Z₁ и Z₂колесу Z₃ необходимо пройти над колесом Z₆.

УсловиеZ₅ – Z₃ ³ 5

Для блока на рис. 1д так же Z₅ – Z₃ ³ 5

Для блока по рис. 1г условия соблюдать не нужно, так как колесо Z₃ не нужно перемещать над колесом Z₆.

Если условие не выполняется, то нужно изменить числа зубьев или использовать конструкцию на рис. 1г или применить иные конструктивные решения.

В соответствии с рис. 2а, так как Z₆ < Z₄, то условие запишется в виде

Z₂ – Z₄ ³ 5

33 – 30 = 3 < 5

Условие переключения не выполняется, следовательно нужно увеличить расчетные числа зубьев. Умножим их на 6, тогда:

Z₂ = 66 Z₄ = 60

Z₂ – Z₄ = 6 > 5,

Следовательно:

Z₁ + Z₂ = Z₃ + Z₄ = Z₅ + Z₆ = 42 + 66= 60 + 48 = 54 + 54 = 108

При проверке возможно изменение схемы переключения или видоизменение структуры графика скоростей. Если условия зацепления удовлетворены, то можно переходить к следующему этапу кинематического расчета коробки.

Дата добавления: 2015-04-24