Поняття про втрату стійкості при напруженнях, що перевищують границю пропорційності

Виведення формули Ейлера ґрунтується на застосуванні диференціаль­ного рівняння пружної лінії. Тому скористатися цією формулою можна лише тоді, коли справедливий закон Гука, тобто доки критичне напруження (напруження стискання, що відповідає критичній силі) не переви­щує границі пропорційності:

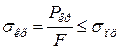. (4.5)

Виведемо формулу для критичного напруження σ_кр. Відповідно до виразів (4.5) та (4.4)

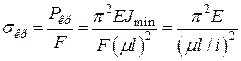. (4.6)

Тут 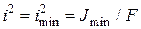– квадрат найменшого з головних радіусів інерції стержня; F = F_бр – площа брутто поперечного перерізу стержня. Ввівши безрозмірну величину

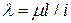, (4.7)

що називається гнучкістю стержня (slenderness ration of a bar), остаточно знайдемо

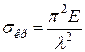, (4.8)

тобто критичне напруження стержня залежить тільки від пружних властивостей матеріалу (модуля пружності Е) та гнучкості стержня λ.

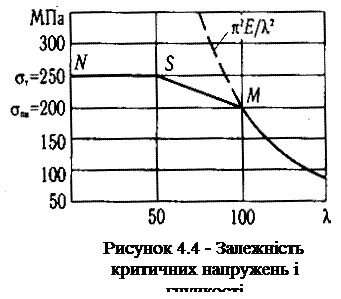Функціональна залежність (4.8) становить видозміну формули Ейлера. У системі координат σ_кр ≈ λ цю залежність можна подати у вигля­ді гіперболічної кривої, що називається гіперболою Ейлера. Як приклад наведе­мо такий графік (рис. 4.4) для стержня зі сталі марки Ст.3, для якої модуль пружності Е = = 2,1∙10⁵ МПа, границя текучості σ _т = 240 МПа, а границя пропорційності σ _пц = 200 МПа. Графік показує, що із зростанням гнучкості стержня критичне напруження прямує до нуля, і навпаки, із наближенням гнучкості стержня до нуля критичне напруження прямує до нескінченності.

Однак з умови (4.5) застосованості формули Ейлера відповідно до формули (4.8) маємо

,

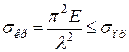і, отже,

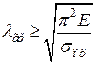. (4.9)

Це означає, що формула Ейлера стає непридатною при гнучкості стержня, меншій за граничне значення λ_гр, яке залежить тільки від власти­востей матеріалу, тобто в розглядуваному прикладі при

λ < .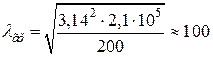

Те саме можна отримати і графічно. Якщо на осі ординат (σ_кр) відкласти значення границі пропорційності (σ _пц = 200 МПа) і провести із отриманої точки К пряму, паралельну осі абсцис, то вона в перетині з гіперболою Ейлера дасть точку М,абсциса якої і є λ_гр. Ліворуч від точки М гіпербо­лу Ейлера зображено штриховою лінією, оскільки вона тут дає значення напружень вищі за границю пропорційності, тобто такі, що не відповіда­ють умовам її застосування.

Проте явище поздовжнього згинання продовжує існувати й за грани­цею пружності. Дослідами встановлено, що дійсні критичні напруження для стержнів середньої та малої гнучкості λ < λ_гр менші, ніж визначені за формулою Ейлера. Отже, в цьому разі формула Ейлера дає завищені значення критичної сили, тобто завжди переоцінює дійсну стійкість стержня. Тому використання формули Ейлера для стержнів, що втрачають стійкість за границею пружності, не тільки принципово неправильне, а й дуже небезпечне за своїми наслідками.

Теоретичне розв'язання задачі про стійкість за границею пропорцій­ності складне, тому зазвичай користуються емпіричними формулами, отриманими в результаті обробки багатьох дослідних даних.

Ф. С. Ясинський зібрав та обробив великий дослідний матеріал щодо поздовжнього згинання стержнів, у результаті чого склав таблицю критичних напружень залежно від гнучкості для низки матеріалів та запропонував просту емпіричну формулу для обчислення критичних напружень за границею пропорційності:

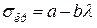. (4.10)

Значення коефіцієнтів а та b для деяких матеріалів наведено в табл. Е.2 (додаток Е). Для чавуну користуються параболічною залежністю

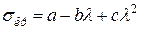, (4.11)

де с = 0,53.

За цими даними для кожного матеріалу при 0 < λ < λ_гр можна побуду­вати графік залежності критичних напружень від гнучкості стержня.

За деяким значенням гнучкості (позначимо його λ₀) напруження σ_кр, обчислене за формулою (4.10) або (4.11), стає таким, що дорівнює граничному напруженню при стисканні, а саме:

для пластичних матеріалів

,

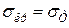для крихких матеріалів

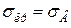. (4.12)

Стержні, в яких λ < λ₀, називають стержнями малої гнучкості. Їх розра­ховують тільки на міцність.

У розглядуваному прикладі (рис. 4.4) частина графіка критичних на­пружень за границею пропорційності (при 50 < λ < 100) має вигляд злегка нахиленої прямої SM, а частина (при 0 < λ < 50) – горизонтальної лінії NS. Отже, графік σ_кр = f(λ) для сталі Ст.3 складається з трьох частин: гіперболи Ейлера при λ > 100, похилої прямої при 50 < λ < 100 та майже горизонтальної прямої при λ < 50. Похила пряма SM відповідає напруженням між границею пропорційності і границею текучості. Горизонталь­на пряма SN відповідає напруженню, що дорівнює границі текучості.

Дата добавления: 2015-03-29