
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 4. Симплексный метод решения задачи линейного программирования
|
|
|
|
Студент должен знать алгоритм решения задач линейного программирования симплексным методом, знать признак бесконечности множества оптимальных планов, признак неограниченности целевой функции, алгоритм решения задач линейного программирования симплексным методом с искусственным базисом. Студент должен уметь применять алгоритм решения задач линейного программирования симплексным методом на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. План, содержащийся в таблице
| базисные переменные | коэф-т целевой функции | свободные члены | 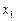
| 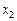
| 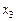
| 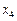
| 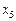
|
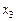
| |||||||
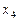
| |||||||
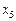
| |||||||
|
1) оптимален
*2) не оптимален
2. В результате решения задачи линейного программирования симплексным методом на нахождение максимального значения получена таблица:
| базисные переменные | коэф-т целевой функции | свободные члены | 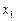
| 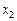
| 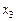
| 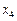
| 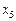
|
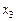
| |||||||
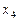
| |||||||
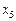
| |||||||
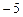
|
Планом, соответствующим таблице, является:
*1) (0; 0; 20; 3; 4)
2) (20; 3; 4; 0; 0)
3) (0; 0; 0)
3. При решении задачи линейного программирования требуется найти максимальное значение целевой функции. Оптимальный опорный план будет получен, если:
1) в индексной строке нет нулевых оценок;
*2) в индексной строке нет отрицательных оценок;
3) в индексной строке нет положительных оценок;
4) в индексной строке хотя бы одна оценка отрицательна.
4. Решается задача линейного программирования на нахождение максимального значения. Некоторый неоптимальный план записан в симплексной таблице.
| базисные переменные | коэф-т целевой функции | свободные члены | 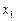
| 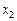
| 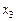
| 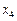
|
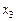
| 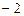
| |||||
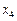
| ||||||
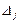
| 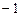
| 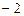
|
В качестве разрешающего элемента при переходе к нехудшему плану нужно выбрать:
1) -2
2) 3
3) 1
*4) 10
5. В результате решения задачи линейного программирования симплексным методом на нахождение максимального значения получена таблица:
| базисные переменные | коэф-т целевой функции | свободные члены | 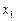
| 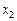
| 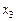
| 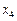
| 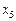
|
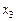
| |||||||
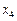
| |||||||
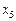
| |||||||
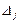
| 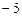
|
План, содержащийся в таблице, не оптимален. Следует ввести в базис переменную:
1) x1
*2) x2
3) x3
4) x4
5) x5
6. В результате решения задачи линейного программирования симплексным методом на нахождение максимального значения получена таблица:
| базисные переменные | коэф-т целевой функции | свободные члены | 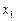
| 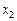
| 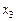
| 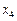
| 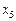
|
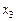
| |||||||
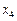
| |||||||
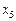
| 
| ||||||
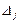
| 
|  0 0
|
Наименьшее симплексное отношение равно:
*1) 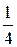 ; 2)
; 2) 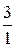 ; 3)
; 3) 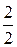 ; 4)
; 4) 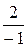
7. Дана первая симплексная таблица решения задачи линейного программирования:
| базисные переменные | коэф-т целевой функции | свободные члены | 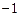
| |||
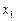
| 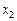
| 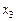
| 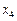
| |||
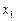
| 
| |||||
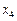
| 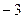
| |||||
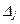
| -4 | ? |
Оценка переменной 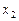 равна
равна
*1) 4·(–1) + 0·1 – (–1)
2) 4·(+1) + 0·1
3) 4·(–1) + 0·1 –1
4) 4·2 + 0·(–3) –0
8. Дана первая симплексная таблица решения задачи линейного программирования:
| базисные переменные | коэф-т целевой функции | свободные члены | 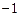
| |||
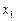
| 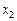
| 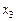
| 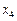
| |||
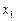
| 
| |||||
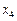
| 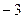
| |||||
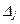
| ? | ? |
Оценка переменной 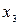 равна
равна
1) 4·(–1) + 0·1 – (–1)
2) 4·(+1) + 0·1
3) 4·(–1) + 0·1 –1
*4) 4·2 + 0·(–3) –0
9. Дана первая симплексная таблица решения задачи линейного программирования:
| базисные переменные | коэф-т целевой функции | свободные члены | 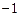
| |||
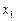
| 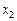
| 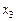
| 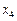
| |||
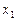
| 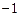
| |||||
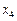
| 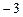
| |||||
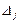
| ? |
Значение целевой функции равно:
1) 4·1 + 0·0
*2) 4·3 + 0·2
3) 4·(–1) + 0·2 –(–1)
10. При решении задачи линейного программирования на нахождение максимального значения с искусственным базисом получили оптимальный план, в котором искусственная переменная равна 3. Какой вывод можно сделать об этом плане?
1) задача имеет бесконечное множество оптимальных планов
*2) система ограничений задачи несовместна, решений нет
3) целевая функция не ограничена сверху
4) целевая функция не ограничена снизу
5) план является оптимальным единственным
Тема 5. Двойственная задача линейного программирования и ее решение
Студент должен знать правила построения двойственной задачи и уметь применять их на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Дана исходная задача линейного программирования:
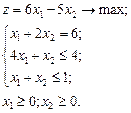
Целевой функцией двойственной задачи является:
1) 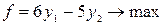
2) 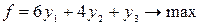
*3) 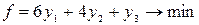
2. 1. Дана исходная задача линейного программирования:
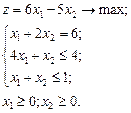
Левые части системы основных ограничений двойственной задачи имеют вид:
*1) 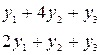 2)
2) 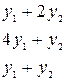 3)
3) 
3. Дана исходная задача линейного программирования:
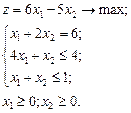
Свободными членами системы основных ограничений двойственной задачи являются:
1) 6; 4; 1 *2) 6; -5 3) 1; 2; 4; 1; 1; 1 4) 4; 1
4. Дана исходная задача линейного программирования:
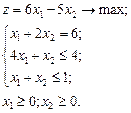
Ограничению 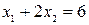 соответствует переменная двойственной задачи
соответствует переменная двойственной задачи 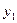 , на которую
, на которую
1) налагается условие неотрицательности
*2) не налагается условие неотрицательности
5. Дана исходная задача линейного программирования:
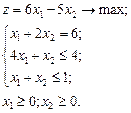
Ограничению 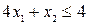 соответствует переменная двойственной задачи, которая принимает
соответствует переменная двойственной задачи, которая принимает
*1) неотрицательное значение
2) отрицательное значение
3) положительное значение
4) любое значение
6. Дана исходная задача линейного программирования:
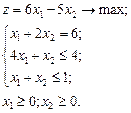
Количество двойственных переменных равно:
1) 1; 2) 2; *3) 3; 4) 4; 5) 5.
8. В начальном опорном плане исходной задачи базисными переменными являются 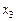 ,
, 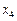 . Таблица, содержащая оптимальный план исходной задачи имеет вид:
. Таблица, содержащая оптимальный план исходной задачи имеет вид:
| базисные переменные | коэф-т целевой функции | свободные члены | 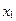
| 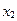
| 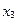
| 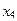
|
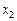
| 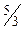
| 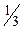
| ||||
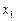
| 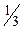
| |||||
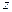
| 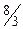
| 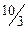
|
Тогда решением двойственной ей задачи будет:
1) y* = (1; 3; 5; 1)
*2) y* = (8/3; 10/3; 0; 0)
3) y* = (0; 0; 8/3; 10/3)
4) y* = (30; 0; 0; 8/3; 10/3)
9. В результате решения задачи симплексным методом получили 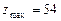 . Целевая функция соответствующей двойственной задачи будет равна:
. Целевая функция соответствующей двойственной задачи будет равна:
1) 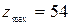 ; 2)
; 2) 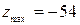 ; *3)
; *3) 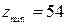 ; 4)
; 4) 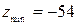 ; 5)
; 5) 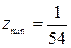 .
.
10. Пусть целевая функция исходной задачи линейного программирования не ограничена. Тогда двойственная к ней задача:
*1) имеет несовместную систему ограничений;
2) имеет единственное оптимальное решение;
3) имеет целевую функцию, неограниченную на множестве планов;
4) имеет бесконечное множество оптимальных планов.
11. Система ограничений исходной задачи линейного программирования несовместна. Тогда двойственная к ней задача:
1) имеет несовместную систему ограничений;
2) имеет единственное оптимальное решение;
*3) имеет целевую функцию, неограниченную на множестве планов;
4) имеет бесконечное множество оптимальных планов.
Тема 6. Транспортная задача линейного программирования
Студент должен знать постановку и алгоритм решения транспортной задачи линейного программирования и уметь применять его при решении задач линейного программирования.
Примерные тестовые задания, предлагаемые в этой теме:
1. В транспортной задаче для трех поставщиков и четырех потребителей составление начального опорного плана осталось незаконченным. Таблица содержит матрицу затрат на перевозки (в правых верхних углах рабочих клеток), потребности потребителей и запасы поставщиков.
| 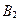
| 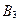
| 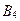
| Запасы | |
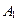
| 25 | 22 | 20 | 22 | |
| 24 | 18 | 19 | 21 | |

| 14 | 15 | 22 | 20 | |
| Потребности |
Чтобы получить опорный план нужно:
1) в клетку А1В3 внести число 7;
*2) в клетку А1В3 внести число 7, в клетку А1В4 внести число 8;
3) в клетку А1В4 внести число 8;
4) в клетку А1В3 внести число 15;
2. В транспортной задаче необходимо спланировать перевозки топлива из четырех хранилищ 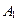 ,
, 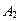 ,
,  ,
, 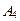 (запасы соответственно равны 12, 5, 10, 8 т) к трем потребителям
(запасы соответственно равны 12, 5, 10, 8 т) к трем потребителям 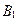 ,
, 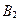 ,
, 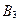 (спрос соответственно равен 2, 7, 30 т) при минимальных затратах. Задача является
(спрос соответственно равен 2, 7, 30 т) при минимальных затратах. Задача является
1) задачей с закрытой моделью
2) задачей с открытой моделью, требующей введения фиктивного потребителя
*3) задачей с открытой моделью, требующей введения фиктивного хранилища
4) другое
3. В транспортной задаче необходимо спланировать перевозки топлива из четырех хранилищ 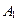 ,
, 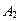 ,
,  ,
, 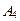 (запасы соответственно равны 12, 5, 8, 15 т) к трем потребителям
(запасы соответственно равны 12, 5, 8, 15 т) к трем потребителям 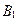 ,
, 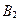 ,
, 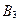 (спрос соответственно равен
(спрос соответственно равен 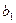 ; 20; 14). Задача имеет решение при
; 20; 14). Задача имеет решение при 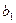 равном:
равном:
*1) 6;
2) 40;
3) 15;
4) 20.
4. Дана матрица затрат транспортной задачи 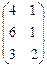 . Получен оптимальный план этой задачи
. Получен оптимальный план этой задачи 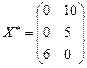 . Целевая функция затрат
. Целевая функция затрат 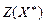 равна:
равна:
1) 10; 2) 15; *3) 33; 4) 18.
5. Таблица транспортной задачи содержит план с вычисленными по формуле 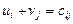 потенциалами, кроме одного, который равен:
потенциалами, кроме одного, который равен:
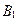
| 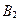
| 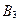
| 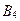
| Запасы | ||
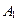
| 25 | 22 | 20 | 22 | 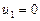
| |
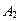
| 24 | 18 | 19 | 21 | 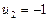
| |

| 14 | 15 | 22 | 20 | 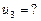
| |
| Потребности | ||||||
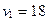
| 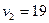
| 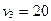
| 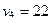
|
1) 20; 2) 14; 3) 0; *4) –4.
6. Таблица содержит план решения (числа в центре рабочих клеток) транспортной задачи для трех поставщиков и четырех потребителей, матрицу затрат на перевозки (в правых верхних углах рабочих клеток), потребности потребителей и запасы поставщиков. По заполненным клеткам найдены значения потенциалов.
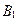
| 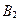
| 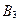
| 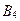
| Запасы | ||
| 14 | 17 | 20 | 22 | 
| |
| 24 | 18 | 19 | 21 | 
| |

| 21 | 15 | 13 | 20 | 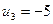
| |
| Потребители | ||||||
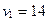
| 
| 
| 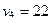
|
Оценка свободной клетки 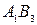 , вычисленная по формуле
, вычисленная по формуле 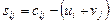 , равна:
, равна:
1) 1; 2) 19; *3) 2; 4) 23; 5) 10
7. В транспортной задаче для трех поставщиков и четырех потребителей произведена оценка свободных клеток (в левом верхнем углу клетки).
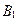
| 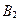
| 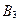
| 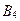
| Запасы | ||
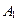
| 14 | 2 19 | 4 20 | –7 20 | 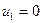
| |
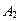
| 4 17 | 18 | 15 | –5 21 | 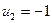
| |

| 11 21 | –2 13 | 12 | 7 23 | 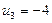
| |
| Потребители | ||||||
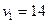
| 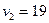
| 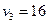
| 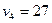
|
Тогда план
1) является оптимальным (решение единственное);
2) является оптимальным (решение не единственное);
*3) не оптимален, наиболее перспективной для загрузки является клетка А1В4;
4) не оптимален, наиболее перспективной для загрузки является клетка А2В4;
5) не оптимален, наиболее перспективной для загрузки является клетка А3В1.
8. Приведена таблица, содержащая неоптимальный план транспортной задачи. После проведенной оценки свободных клеток наиболее перспективной признана клетка 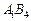 , и выделен цикл перераспределения груза.
, и выделен цикл перераспределения груза.
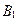
| 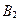
| 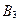
| 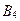
| Запасы | ||
   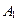
| 14 | 2 19 | 4 20 | -7 20 | 
| |
  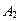
| 4 17 | 18 | 15 | -5 21 | 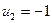
| |
 
| 11 21 | -2 13 | 12 | 7 23 | 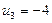
| |
| Потребители | ||||||
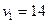
| 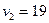
| 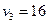
| 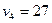
|
Тогда клетка 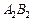 должна содержать количество груза, равное:
должна содержать количество груза, равное:
1) 30; 2) 0; *3) 40; 4) 15.
9. При решении транспортной задачи получили оптимальный план, причем, одна из оценок свободных клеток равна нулю. Тогда план
1) является оптимальным (решение единственное);
*2) является оптимальным (решение не единственное);
3) другое.
10. В транспортной задаче все оценки свободных клеток строго больше нуля. Тогда план
*1) является оптимальным (решение единственное);
2) является оптимальным (решение не единственное);
3) план не оптимален;
4) другое.
11. Приведена таблица, содержащая план транспортной задачи для трех поставщиков и четырех потребителей.
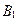
| 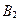
| 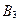
| 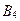
| Запасы | |
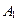
| 20 | 22 | 10 | 11 | ? |
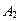
| 19 | 18 | 19 | 21 | ? |

| 14 | 15 | 16 | 20 | ? |
| Потребители |
Запасы поставщиков 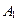 ,
, 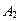 ,
,  соответственно равны:
соответственно равны:
1) 14, 16, 12; *2) 14, 33, 12; 3) 14, 11, 11.
12. Приведена таблица, содержащая план транспортной задачи для трех поставщиков и четырех потребителей.
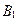
| 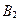
| 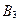
| 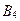
| Запасы | |
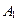
| 20 | 22 | 10 | 11 | |
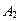
| 19 | 18 | 19 | 21 | |

| 14 | 15 | 16 | 20 | |
| Потребители | ? | ? | ? | ? |
Спрос потребителей 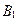 ,
, 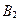 ,
, 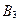 ,
, 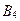 соответственно равен:
соответственно равен:
*1) 11, 16, 25, 10; 2) 11, 10, 15, 10; 3) 0, 0, 10, 0.
13. Приведена таблица, содержащая неоптимальный план транспортной задачи. После проведенной оценки свободных клеток наиболее перспективной признана клетка 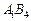 , и выделен цикл перераспределения груза.
, и выделен цикл перераспределения груза.
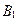
| 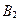
| 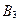
| 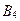
| Запасы | ||
   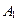
| 14 | 2 19 | 4 20 | -7 20 | 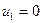
| |
  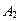
| 4 17 | 18 | 15 | -5 21 | 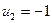
| |
 
| 11 21 | -2 13 | 12 | 7 23 | 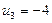
| |
| Потребители | ||||||
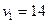
| 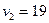
| 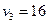
| 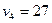
|
Объем перераспределяемого по циклу груза равен:
1) 20; 2) 30; *3) 5; 4) 35.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1612; Нарушение авторских прав?; Мы поможем в написании вашей работы!