Теоретические сведения. Цель работы: определение емкости конденсаторов и проверка законов последовательного и параллельного соединений конденсаторов

С ПОМОЩЬЮ ВОЛЬТМЕТРА

ОПРЕДЕЛЕНИЕ ЕМКОСТИ КОНДЕНСАТОРА

Цель работы: определение емкости конденсаторов и проверка законов последовательного и параллельного соединений конденсаторов.

Приборы и оборудование: источник питания, вольтметр, потенциометр (R), эталонный конденсатор (С_эт), исследуемые кон­денсаторы (С_х1 и С_х2), переключатели.

Опытным путем было установлено, что в природе существует два типа электрических зарядов, условно названных положительными и отрицательны­ми. Одноименные заряды отталкиваются друг от друга, разноименные притя­гиваются.

Р. Милликен доказал, что электрический заряд дискретен, т.е. величина за­ряда любого тела составляет целое число, кратное элементарному электриче­скому заряду е (e=1,6∙10^-19 Кл). Электрон и протон являются соответственно носителями элементарных отрицательного и положительного зарядов.

В результате обобщения опытных данных был сформулирован фундамен­тальный закон природы - закон сохранения заряда: алгебраическая сумма элек­трических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри нее.

Единица электрического заряда, 1 кулон (Кл) - это электрический заряд, проходящий через поперечное сечение проводника при силе тока в 1 А за время, рапное 1с:

1Кл=1 А∙1с.

Закон взаимодействия неподвижных точечных электрических зарядов был открыт Кулоном: сила взаимодействия F двух точечных зарядов прямо пропор­циональна величине зарядов q₁ и q₂ и обратно пропорциональна квадрату расстояния r между ними:

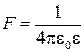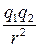∙ , (1)

где 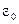=8,85×10^-12 Ф/м - электрическая постоянная; 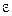- диэлектрическая проницаемость среды (безразмерная величина).

Напряженность 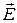электрического поля в данной точке есть физическая величина, определяемая силой, действующей на единичный положительный заряд, помещенный в эту точку:

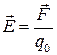. (2)

Направление вектора 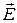совпадает с направлением силы, действующей на положительный заряд. Выражение для определения единицы напряжен­ности электрического поля:

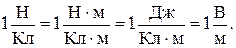(3)

Графически электростатическое поле изображают с помощью линий нап­ряженности (силовых линий), которые проводят так, чтобы касательные к ним в каждой точке пространства совпадали по направлению с вектором напряженно­сти (рис. I).

Величина

называется потоком вектора напряженности через площадку d S. Здесь 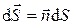- вектор, модуль которого равен d S, а направление совпадает с нор­малью n к площадке d S ().

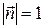Электростатические поля подчиняются принципу суперпозиции: напря­женность 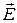результирующего поля, созданного системой зарядов, равна гео­метрической сумме напряженностей полей, созданных в данной точке каждым из зарядов в отдельности:

, (4)

где 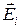- напряженность электростатического поля, созданного i -м зарядом.

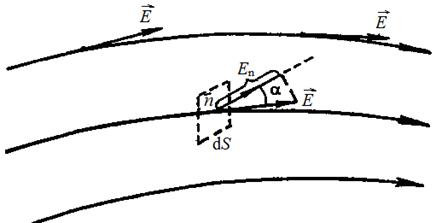
Рис. 1

Теорема Остроградского-Гаусса для электростатического поля в вакууме звучит так: поток вектора напряженности электростатического поля через про­извольную замкнутую поверхность в вакууме равен алгебраической сумме за­ключенных внутри этой поверхности зарядов, деленной на e₀:

. (5)

Из теоремы Гаусса следует, что напряженность электростатического поля между двумя бесконечными параллельными и разноименно заряженными плоскостями в вакууме будет равна

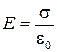, (6)

где 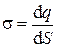- поверхностная плотность заряда плоскостей.

Если между заряженными плоскостями находится изолятор с диэлектриче­ской проницаемостью 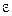, то напряженность поля внутри него уменьшается в 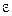раз (рис. 2):

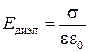. (7)

Электростатическое поле является полем консервативных сил, т.е. работа, совершаемая силами поля по перемещению электрического заряда из одной точки пространства в другую, не зависит от траектории движения заряда, а оп­ределяется только его начальным и конечным положениями. Для такого рода полей можно ввести понятие потенциальной энергии заряда, численно равной работе, совершаемой силами электростатического поля по перемещению его из данной точки пространства в другую (ту, в которой потенциальная энергия заряда равна нулю).

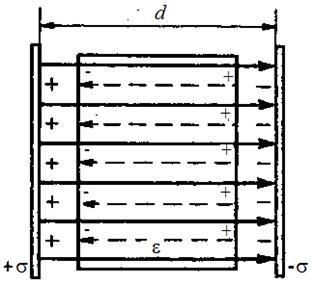
Рис. 2

Как правило, потенциальная энергия заряда, удаленного в бесконечность, считается равной нулю. Поэтому она будет равна

, (8)

где 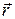- радиус-вектор; 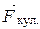- кулоновская сила; 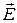- напряжен­ность электростатического поля; q₀ - электрический заряд.

Если заряд q ₀ перемещается из первой точки во вторую(определяются со­ответственно радиус-векторам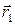и и 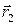то работу, совершаемую силами по­ля, можно найти как разность работ

(9)

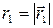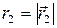где и ; и - работы, совершаемые силами поля при перемещении заряда из первой и второй точек в бесконечность.

Потенциал – физическая величина, определяемая работой сил поля по пе­ремещению единичного положительного заряда из данной точки в беско­нечность:

. (10)

Единица потенциала - вольт (В): 1 В - потенциал такой точки поля, в ко­торой заряд в 1Кл обладает потенциальной энергией в 1 Дж:

.

Поскольку , то

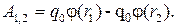(11)

Отсюда

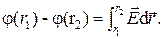(12)

Зная потенциал в каждой точке пространства можно найти напряженность электростатического поля:

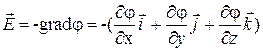. (13)

Знак «минус» указывает на то, что вектор напряженности 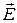направлен в сторону убывания потенциала.

Потенциал уединенного проводника прямо пропорционален его заряду;

.

При этом величину

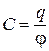(14)

называют электроемкостью уединенного проводника. Единица электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, потенциал которо­го изменяется на 1В при сообщении ему заряда в 1Кл, т.е.

. (15)

Для накопления значительных зарядов служат конденсаторы, состоящие из двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы подразделяются на плоские, цилиндрические и сферические. Под емкостью конденсатора понимается физическая величина, равная отношению накопленного заряда q к разности потенциалов 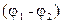между обкладками:

(16)

где 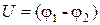напряжение между обкладками. Плоский конденсатор обладает емкостью

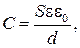(17)

где 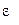- диэлектрическая проницаемость изолятора; 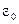- электрическая постоян­ная; S - площадь обкладки; d - расстояние между обкладками.

Для увеличения емкости и варьирования ее возможных значений конден­саторы соединяют в батареи параллельно или последовательно. У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна 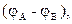см. рис. 3.

Рис. 3

Если емкости отдельных конденсаторов то их заряды равны со­ответственно

(18)

а заряд батареи конденсаторов

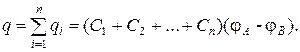
Полная емкость батареи

, (19)

т.е. при параллельном соединении конденсаторов она равна сумме емкостей от­дельных конденсаторов.

У последовательно соединенных конденсаторов заряды всех обкладок рав­ны по модулю, а разность потенциалов на зажимах батареи, см. рис. 4, равна

. (20)

Причем для любого из рассматриваемых конденсаторов

^.

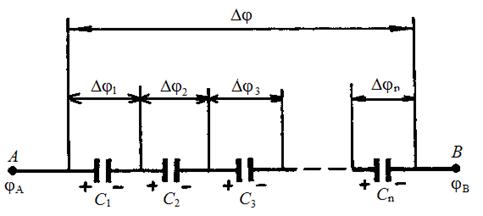
Рис. 4

С другой стороны,

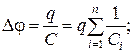(21)

откуда , (22)

т.е. при последовательном соединении конденсаторов суммируются обратные величины емкостей.

Если дана емкость эталонного конденсатора С _эт, то неизвестную емкость другого конденсатора С _х можно определить следующим образом.

Сначала конденсатор С _эт зарядить от источника постоянного тока (рис.5, а). При этом накапливается заряд q. С помощью вольтметра измерить напряже­ние на обкладках конденсатора:

Тогда

.

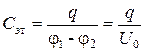Отсюда

_. (23)

Затем эталонный конденсатор отключить от источника питания и к нему параллельно присоединить конденсатор неизвестной емкости С_х (рис. 5, б). Электрический заряд q распределится по конденсаторам С _эт и С _х.

Согласно закону сохранения зарядов в замкнутой системе

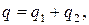(24)

где q₁, q₂ - электрические заряды на конденсаторах С _эти С _х.

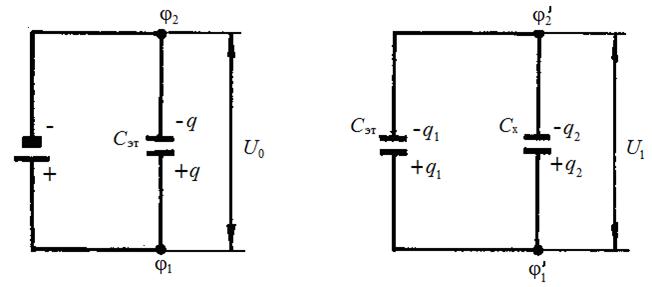
Рис. 5, а Рис. 5, б

После этого измерить напряжение на обкладках конденсаторов, причем

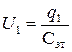и .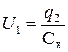

Отсюда

и . (25)

Поэтому

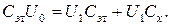
В результате (26)

Дата добавления: 2015-03-29