Основы теории зацепления

Классификация зубчатых передач

Зубчатые передачи

Зубчатой передачей называется трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, или колесо и рейка с зубьями, образующими с неподвижным звеном (корпусом) вращательную или поступательную пару.

Зубчатая передача служит для передачи вращательного движения с одного вала на другой и изменения частоты вращения посредством зубчатых колес и реек.

Зубчатое колесо, сидящее на передающем вращение валу, называется веду­щим, а на получающем вращение — ведомым.

Меньшее из двух колес со­пряженной пары называют шестерней; большее — колесом;

термин «зубчатое колесо» является общим. Параметрам шестерни приписывают индекс 1, а параметрам колеса – 2.

Основными преимуществами зубчатых передач являются:

- постоянство передаточного числа (отсутствие проскальзывания);

- компактность по сравнению с фрикционными и ременными передачами;

- высокий КПД (до 0,97…0,98 в одной ступени);

- большая долговечность и надежность в работе (например, для редукторов общего применения установлен ресурс ~ 30 000 ч);

- возможность применения в широком диапазоне скоростей (до 150 м/с), мощностей (до десятков тысяч кВт).

Недостатки:

- шум при высоких скоростях;

- невозможность бесступенчатого изменения передаточного числа;

- необходимость высокой точности изготовления и монтажа;

- незащищенность от перегрузок;

- наличие вибраций, которые возникают в результате неточного изготовления и неточной сборки передач.

По расположению осей валов различают передачи с параллельными (рис. 2.1, а – в, з), с пересекающимися (рис. 2.1, г, д) и перекрещивающимися (рис. 2.1, е, ж) геометрическими осями.

По форме могут быть цилиндрические (рис. 2.1, а – в, з), конические (рис. 2.1, г, д, ж), эллиптические, фигурные зубчатые колеса и колеса с неполным числом зубьев (секторные).

По форме профилей зубьев различают эвольвентные и круговые передачи, а по форме и расположению зубьев – прямые (рис. 2.1, а, г, е, з), косые (рис. 2.1, б), шевронные (рис. 2.1, в) и круговые (рис. 2.1, д, ж).

В зависимости от относительного расположения зубчатых колес передачи могут быть с внешним (рис. 2.1, а) или внутренним (рис. 2.1, з) их зацеплением. Для преобразования вращательного движения в возвратно поступательное и наоборот служит реечная передача (рис. 2.1, е).

Зубчатые передачи эвольвентного профиля широко распространены во всех отраслях машиностроения и приборостроения. Они применяются в исключительно широком диапазоне условий работы. Мощности, передаваемые зубчатыми передачами, изменяются от ничтожно малых (приборы, часовые механизмы) до многих тысяч кВт (редукторы авиационных двигателей). Наибольшее распространение имеют передачи с цилиндрическими колесами, как наиболее простые в изготовлении и эксплуатации, надежные и малогабаритные. Конические, винтовые и червячные передачи применяют лишь в тех случаях, когда это необходимо по условиям компоновки машины.

Эвольвента окружности и ее свойства.

Эволютой называется геометрическое место центров кривизны данной кривой. Данная кривая по отношению к эволюте называется эвольвентой. Согласно определению нормаль к эвольвенте (на которой лежит центр кривизны) является касательной к эволюте. Эвольвенты окружности описываются точками производящей прямой при ее перекатывании по окружности, которую называют основной.

Свойства эвольвенты окружности:

Форма эвольвенты окружности определяется только радиусом основной окружности r_b. При 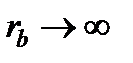эвольвента переходит в прямую линию.

Производящая прямая является нормалью к эвольвенте в рассматриваемой произвольной точке M_y. Отрезок нормали в произвольной точке эвольвенты l_MyN = r равен радиусу ее кривизны и является касательной к основной окружности.

Эвольвента имеет две ветви и точку возврата М₀, лежащую на основной окружности. Эвольвента не имеет точек внутри основной окружности.

Точки связанные с производящей прямой но не лежащие на ней при перекатывании описывают: точки расположенные выше производящей прямой W - укороченные эвольвенты, точки, расположенные ниже производящей прямой L - удлиненные эвольвенты.

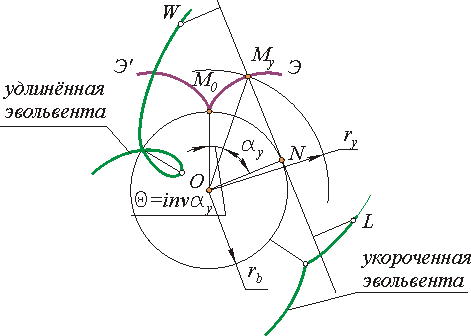
Рис. 5.1

Если производящая прямая задана параметрическими уравнениями х = x (t), y = y (t), то параметрические уравнения её эволюты будут следующие:

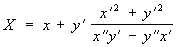
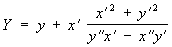
Эвольвентное зацепление и его свойства.

В зубчатой передаче контактирующие элементы двух профилей выполняются по эвольвентам окружности и образуют, так называемое эвольвентное зацепление. Это зацепление обладает рядом полезных свойств, которые и определяют широкое распространение эвольвентных зубчатых передач в современном машиностроении. Рассмотрим эти свойства.

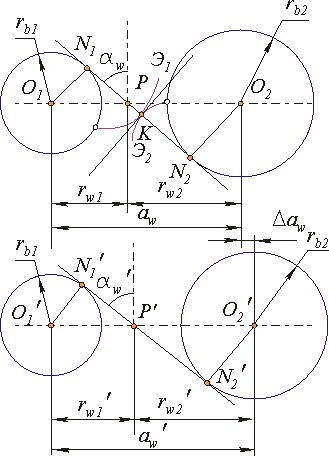
Рис. 1

Свойство 1. Передаточное отношение эвольвентного зацепления определяется только отношением радиусов основных окружностей и является величиной постоянной.

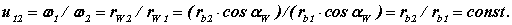
Свойство 2. При изменении межосевого расстояния в эвольвентном зацеплении его передаточное отношение не изменяется.

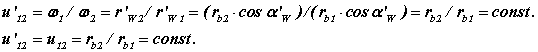
Свойство 3. При изменении межосевого расстояния в эаольвентном зацеплении величина произведения межосевого расстояния на косинус угла зацепления не изменяется.

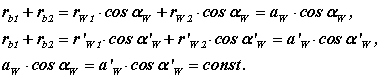
Свойство 4. За пределами отрезка линии зацепления N₁N₂ рассматриваемые ветви эвольвент не имеют общей нормали, т. е. профили выполненные по этим кривым будут не касаться, а пересекаться. Это явление называется интерференцией эвольвент или заклиниванием.

Классификация зубчатых передач приведена на рис 2.2.

Классификация по взаимному расположению осей колес: с па­раллельными осями (цилиндрическая передача — рис. 172, I—IV); с пере­секающимися осями (коническая передача — рис. 172, V, VI); со скрещива­ющимися осями (винтовая передача — рис. 172, VII; червячная передача — рис. 172, VIII).

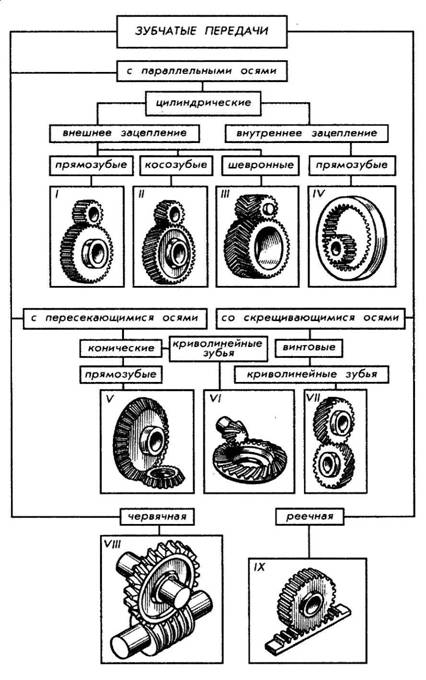
Рис 2. Классификация зубчатых передач

В зависимости от относительного вращения колес и расположения зубьев различают передачи с внеш­ним и внутренним зацеплением. В первом случае (рис. 2, I—III) враще­ние колес происходит в противоположных направлениях, во втором (рис. 2, IV) — в одном направлении. Реечная передача (рис. 2, IX) служит для преобразования вращательного движения в поступательное.

По форме профиля различают зубья эвольвентные (рис. 2, I, II) и неэвольвентные, например цилиндрическая передача Новикова, зу­бья колес которой очерчены дугами окружности.

В зависимости от расположения теоретичес­кой линии зуба различают колеса с прямыми зубьями (рис. 2, I), косыми (рис. 2, II), шевронными (рис.2, III) и винтовыми (рис. 2, IV). В непрямозубых передачах возрастает плавность работы, уменьшается износ и шум. Благодаря этому непрямозубые передачи большей частью применяют в установках, требующих высоких окружных скоростей и пере­дачи больших мощностей.

По конструктивному оформлению различают закры­тые передачи, размещенные в специальном непроницаемом корпусе и обес­печенные постоянной смазкой из масляной ванны, и открытые, работаю­щие без смазки или периодически смазываемые консистентными смазками (рис. 174).

По величине окруж­ной скорости различают: тихо­ходные передачи (v равной до 3 м/с), среднескоростные (v равной от 3... 15 м/с) и быстроходные (v более 15 м/с)

Боковые грани зубьев, соприкасаю­щиеся друг с другом во время враще­ния колес, имеют специальную кри­волинейную форму, называемую про­филем зуба. Наиболее распространен­ным в машиностроении является эвольвентный профиль (рис. 175) Придание профилям зубьев зубча­тых зацеплений таких очертаний не является случайностью. Чтобы зубья двух колес, находящихся в зацепле­нии, могли плавно перекатываться один по другому, необходимо было вы­брать такой профиль для зубьев, при котором не происходило бы перекосов и защемления головки одного зуба во впадине другого.

На рис. 176 изображена пара зубчатых колес, находящихся в зацепле­нии. Линия, соединяющая центры колес О₁ и О₂ называется линией центров или межосевым расстоянием — a_w Точка Р касания начальных окружностей d_W1 и d_W2 — полюс — все­гда лежит на линии центров. Начальными называются окружнос­ти, касающиеся друг друга в полюсе зацепления имеющие общие с зуб­чатыми колесами центры и перекатывающиеся одна по другой без сколь­жения

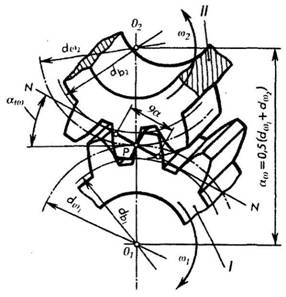Если проследить за движением пары зубьев двух колес с момен­та, когда они впервые коснутся друг друга до момента, когда они выйдут из зацепления, то ока­жется, что все точки касания их в процессе движения будут лежать на одной прямой NN. Прямая NN, проходящая через полюс за­цепление Р и касательная к ос­новным* окружностям db₁, db₂, двух сопряженных колес, назы­вается линией зацепле­ния. Отрезок g_a линии зацепле­ния, отсекаемый окружностями выступов сопряженных колес, — активная часть линии зацепле­ния, определяющая начало и ко­нец зацепления пары сопряжен­ных зубьев

Во время работы цилиндри­ческой прямозубой передачи сила давления Р_n ведущей шес­терни O₁ в начале зацепления передается ножкой зуба на со­пряженную боковую поверх­ность (контактную линию) головки ведомого колеса О₂. Чем больше пара зубьев одновременно находится в зацеплении, тем более плавно работает передача, тем меньшую нагрузку воспринимает на себя каждый зуб.

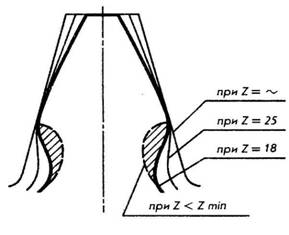
Стремление сделать зубчатую передачу более компактной вызывает не­обходимость применять зубчатые колеса с возможно меньшим числом зубь­ев. Изменение количества зубьев зубчатого колеса влияет на их форму (рис. 177). При увеличе­нии числа зубьев до бесконечно­сти колесо превращается в рейку и зуб приобретает пря­молинейное очертание. С умень­шением числа зубьев одновре­менно уменьшается толщина зу­ба у основания и вершины, а так­же увеличивается кривизна эвольвентного профиля, что приводит к уменьшению проч­ности зуба на изгиб. При умень­шении числа зубьев, когда z < z_mim, происходит так называе­мое подрезание зубьев, то есть явление, когда зубья большого колеса при вращении заходят в область ножки меньшего колеса (см. заштрихованная площадь на рис. 177), тем самым ослабляя зуб в самом опасном сечении, увеличивая износ зубьев и снижая КПД передачи.

На практике подрезку зубьев предотвращают прежде всего выбором со­ответствующего числа зубьев. Наименьшее число зубьев (z_min), при кото­ром еще не происходит подрезание, рекомендуется выбирать от 35 до 40 при равном 15° и от 18 до 25 при 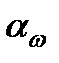равном 20°

В отдельных случаях приходится выполнять передачу с числом зубьев меньшим, чем рекомендуется, при этом производят исправление, или, как говорят, корригирование формы зубьев. Один из таких способов заключает­ся в изменении высоты головки и ножки зуба до h_a = 0,8m; h_f = m. Этот спо­соб исключает подрезку, но увеличивает износ зубьев.

Теперь обратимся к изложению основной теоремы зацепления: общая нормаль (линия зацепления NN) к сопряженным профилям зубьев делит межосевое расстояние (а_w= О₁О₂) на отрезки (О₁Р и 0₂Р), обратно пропор­циональные угловым скоростям (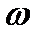 ₁ и 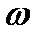₂). Если положение точки Р (полю­са зацепления) неизменно в любой момент зацепления, то передаточное от­ношение — отношение частоты вращения ведущего колеса к частоте враще­ния ведомого — будет постоянным

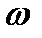О₂Р / O₁P = ₁/ 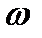₂ = i = const

5.6. Основные элементы зубчатых зацеплений.

При изменении осевого расстояния а_w = О₁О₂ пары зубчатых колес будет меняться и положение по­люса зацепления Р на линии центров, а следовательно, и величина диаметров начальных окружностей, то есть у пары сопряженных зубчатых колес может быть бесчисленное множество начальных окружностей. Следует отметить, что понятие начальные окружности относится лишь к паре со­пряженных зубчатых колес. Для отдельно взятого зубчатого колеса нельзя говорить о начальной окружности

Если заменить одно из колес зубчатой рейкой, то для каждого зубчатого колеса найдется только одна окружность, катящаяся по начальной прямой рейке без скольжения, — эта окружность называется делительной

Так как у каждого зубчатого колеса имеется только одна делительная ок­ружность, то она и положена в основу определения основных параметровзубчатой передачи по ГОСТ 16530- 83 и ГОСТ 16531-83

(рис. 178)

5.7. Основные параметры зубчатых колес:

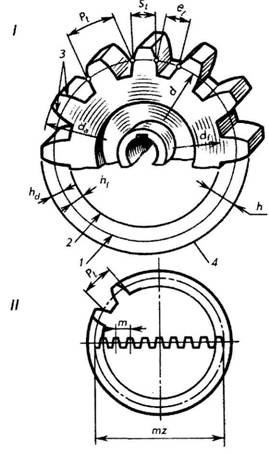
1. Делительными окружностя­ми пары зубчатых колес называ­ются соприкасающиеся окружно­сти, катящиеся одна по другой без скольжения. Эти окружности, на­ходясь в зацеплении (в передаче), являются сопряженными. На чер­тежах диаметр делительной ок­ружности обозначают буквой d.

2. Окружной шаг зубьев Р_t — расстояние (мм) между одноимен­ными профильными поверхностя­ми соседних зубьев. Шаг зубьев, как нетрудно представить, равен делительной окружности, разде­ленной на число зубьев z.

3. Длина делительной окруж­ности. Модуль.

Длину делитель­ной окружности можно выразить через диаметр и число зубьев:

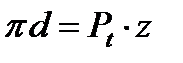
Отсюда диаметр делитель­ной окружности

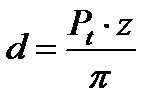
Отношение 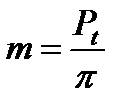называется модулем зубчатого зацепления и обозначается буквой m. Тогда диаметр дели­тельной окружности можно выразить через модуль и число зубьев 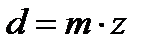. Отсюда .

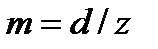Значение модулей для всех передач — вели­чина стандартизированная.

Для понимания зависимости между вели­чинами Р_t 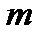и d приведена схема на рис. 178, II, где условно показано размещение всех зубь­ев 2 колеса по диаметру ее делительной окруж­ности в виде зубчатой рейки.

4. Высота делительной головки зуба h_a — расстояние между делительной окружностью колеса и окружностью вершин зубьев.

5. Высота делительной ножки зуба h_f — расстояние между делительной окружностью колеса и окружностью впадин.

6. Высота зуба h — расстояние между ок­ружностями вершин зубьев и впадин цилинд­рического зубчатого колеса h = h_a + h_f..

7. Диаметр окружности вершин зубьев d_a — диаметр окружности, ограничивающей вершины головок зубьев.

8. Диаметр окружности впадин зубьев d_f — диаметр окружности, прохо­дящей через основания впадин зубьев.

При конструировании механизма конструктор рассчитывает величину модуля т для зубчатой передачи и, округлив, подбирает модуль по таблице стандартизированных величин. Затем он определяет величины остальных геометрических элементов зубчатого колеса.

Дата добавления: 2015-04-25