Математическое описание усилительных устройств

Передаточные функции усилительных устройств. Основой для проведения анализа свойств существующих и синтеза новых усилительных устройств с заданными характеристиками является их математическое описание или математическая модель. Основным вопросом, с которым приходится сталкиваться при составлении математической модели, является вопрос ее адекватности реально существующему объекту. Выбранная математическая модель должна, с одной стороны, отражать свойства реального объекта с требуемой степенью точности, а с другой стороны, быть не слишком сложной, что предопределяет получение конечного результата доступными средствами.

В общем случае элементы, используемые для построения усилительных устройств, имеют нелинейные характеристики, причем их параметры зависят как от времени, так и от внешних условий эксплуатации. Поэтому точное математическое описание усилительных устройств достаточно громоздко и базируется на использовании систем нелинейных дифференциальных уравнений, параметры которых зависят от времени и различных внешних возмущающих воздействий.

Однако в большинстве практических случаев этими зависимостями можно пренебречь и с точки зрения математического описания рассматривать усилительное устройство как непрерывную, линейную стационарную систему с сосредоточенными параметрами и детерминированным законом управления.

Непрерывной называется система, в которой все сигналы ее устройств и объектов регулирования являются непрерывными функциями времени; линейной - система, для которой справедлив принцип суперпозиции; стационарной - система, параметры и характеристики которой не зависят от времени. Детерминированным называется закон управления, предполагающий однозначную связь между входным воздействием и соответствующим значением выходного параметра.

Тогда для математического описания усилительного устройства можно воспользоваться системой дифференциальных уравнений с постоянными коэффициентами. Учитывая, что нас, интересует реакция усилительного устройства на некоторое входное воздействие, исходная система дифференциальных уравнений может быть приведена к одному уравнению высокого порядка вида:

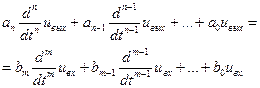, (2.1.8)

где 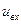и - мгновенное значение входного возмущения и выходного сигнала соответственно, 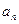и 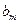- постоянные коэффициенты, содержащие суммы и произведения параметров элементов, входящих в состав усилительного устройства (например, R, L и C).

Воспользовавшись операторной формой записи уравнений, т. е. обозначив 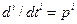, уравнение (2.1.8) можно представить в виде:

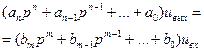. (2.1.9)

Уравнение (2.1.9) позволяет получить передаточную функцию усилительного устройства по выбранному входному возмущению, под которой понимается выражение:

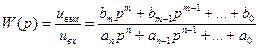. (2.1.10)

Дата добавления: 2015-03-29