Системы счисления

Арифметические основы ЭВМ

Безусловно, одним из основных направлений применения компьютеров были и остаются разнообразные вычисления. Обработка числовой информации ведется и при решении задач, на первый взгляд не связанных с какими-то расчетами, например, при использовании компьютерной графики или звука.

В связи с этим встает вопрос о выборе оптимального представления чисел в компьютере. Безусловно, можно было бы использовать 8-битное (байтовое) кодирование отдельных цифр, а из них составлять числа. Однако такое кодирование не будет оптимальным, что легко увидеть из простого примера. Пусть имеется двузначное число 13. При 8-битном кодировании отдельных цифр в кодах ASCII его представление выглядит следующим образом: 0011000100110011, т.е. код имеет длину 16 битов; если же определять это число просто в двоичном коде, то получим 4-битную цепочку 1101.

Важно, что представление определяет не только способ записи данных (букв или чисел), но и допустимый набор операций над ними; в частности, буквы могут быть только помещены в некоторую последовательность (или исключены из нее) без изменения их самих; над числами же возможны операции, изменяющие само число, например, извлечение корня или сложение с другим числом.

Представление чисел в компьютере имеет две особенности:

□ числа записываются в двоичной системе счисления (в отличие от привычной десятичной);

□ для записи и обработки чисел отводится конечное количество разрядов (в "некомпьютерной" арифметике такое ограничение отсутствует).

Следствия, к которым приводят эти отличия, и рассматриваются в данной главе.

(Страница33)

Начнем с некоторых общих замечаний относительно понятия число [12]. Можно считать, что любое число имеет значение (содержание) и форму представления.

Значение числа задает его отношение к значениям других чисел ("больше", "меньше", "равно") и, следовательно, порядок расположения чисел на числовой оси. Форма представления, как следует из названия, определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значение числа является инвариантом, т. е. не зависит от способа его представления. Это означает также, что число с одним и тем же значением может быть записано по-разному, т. е. отсутствует взаимно однозначное соответствие между представлением числа и его значением.

В связи с этим возникают вопросы, во-первых, о формах представления чисел и, во-вторых, о возможности и способах перехода от одной формы к другой.

Способ представления числа определяется системой счисления.

Определение_________________________________________________

Система счисления — это правило записи чисел с помощью заданного набора специальных знаков — цифр.

Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп: унарная, непозиционные и позиционные.

Унарная — это система счисления, в которой для записи чисел используется только один знак — | (вертикальная черта, палочка). Следующее число получается из предыдущего добавлением новой палочки: их количество (сумма) равно самому числу. Унарная система важна в теоретическом отношении, поскольку в ней число представляется наиболее простым способом и, следовательно, просты операции с ним. Кроме того, именно унарная система определяет значение целого числа количеством содержащихся в нем единиц, которое, как было сказано, не зависит от формы представления.

Из непозиционных наиболее распространенной можно считать римскую систему счисления. В ней некоторые базовые числа обозначены заглавными латинскими буквами: 1 — I, 5 — V, 10 — X, 50 — L, 100 — С, 500 — D, 1000 – М. Все другие числа строятся комбинаций базовых в соответствии со следующими правилами:

□ если цифра меньшего значения стоит справа от большей цифры, то их значения суммируются; если слева — то меньшее значение вычитается из большего;

□ цифры I, X, C и М могут следовать подряд не более трех раз каждая;

□ цифры V, L и D могут использоваться в записи числа не более одного раза.

(Страница34)

Например, запись XIX соответствует числу 19, MDXLIX — числу 1549. Запись чисел в такой системе громоздка и неудобна, но еще более неудобным оказывается выполнение в ней даже самых простых арифметических операций. Отсутствие нуля и знаков для чисел больше М не позволяют римскими цифрами записать любое число (хотя бы натуральное). По указанным причинам теперь римская система используется лишь для нумерации.

В настоящее время для представления чисел применяют, в основном, позиционные системы счисления.

Определение_________________________________________________

Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

Наиболее распространенной и привычной является система счисления, в которой для записи чисел используется 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, Число представляет собой краткую запись многочлена, в который входят степени некоторого другого числа — основания системы счисления. Например:

575, 15=5*10²+7*10¹+5*10⁰+1*10 ^{- 1}+5*10 ^{- 2}

В данном числе цифра 5 встречается трижды, однако значение этих цифр различно и определяется их положением (позицией) в числе. Количество цифр для построения чисел, очевидно, равно основанию системы счисления. Также очевидно, что максимальная цифра на 1 меньше основания. Причина широкого распространения именно десятичной системы счисления понятна — она происходит от унарной системы с пальцами рук в качестве "палочек",

Однако в истории человечества имеются свидетельства использования и других систем счисления — пятеричной, шестеричной, двенадцатиричной, двадцатиричной и даже шестидесятиричной. Общим для унарной и римской систем счисления является то, что значение числа в них определяется посредством операций сложения и вычитания базисных цифр, из которых составлено число, независимо от их позиции в числе. Такие системы получили название аддитивных.

В отличие от них позиционное представление следует считать аддитивно-мультипликативным, поскольку значение числа определяется операциями умножения и сложения. Главной же особенностью позиционного представления является то, что в нем посредством конечного набора знаков (цифр, разделителя десятичных разрядов и обозначения знака числа) можно записать неограниченное количество различных чисел. Кроме того, в позиционных системах гораздо легче, чем в аддитивных, осуществляются операции умножения и деления. Именно эти обстоятельства обуславливают доминирование позиционных систем при обработке чисел, как человеком, так и компьютером.

По принципу, положенному в основу десятичной системы счисления, очевидно, можно построить системы с иным основанием. Пусть p — основание системы счисления. Тогда любое число Z (пока ограничимся только целыми числами), удовлетворяющее условию Z<p^k (k>0, целое), может быть представлено в виде многочлена со степенями (при этом, очевидно, максимальный показатель степени будет равен k-1):

(3.1)

Из коэффициентов a _j при степенях основания строится сокращенная запись числа:

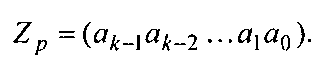
Индекс p числа Z указывает, что оно записано в системе счисления с основанием р: общее число цифр числа равно k. Все коэффициенты a _j — целые числа, удовлетворяющие условию: 0< a_j< р-1.

Уместно задаться вопросом: каково минимальное значение р? Очевидно, р =1 невозможно, поскольку тогда все a_j =0 и форма (3.1) теряет смысл.

Первое допустимое значение р =2 — оно и является минимальным для позиционных систем.

Система счисления с основанием 2 называется двоичной. Цифрами двоичной системы являются 0 и 1, а форма (3.1) строится по степеням 2. Интерес именно к этой системе счисления связан с тем, что, как указывалось выше, любая информация в компьютерах представляется с помощью двух состояний — 0 и 1, которые легко реализуются технически.

Наряду с двоичной в компьютерах используются восьмеричная и шестнадцатеричная системы счисления — причины будут рассмотрены далее.

Дата добавления: 2015-04-25