Алгебраическое сложение в обратном коде

Очевидно, что при отсутствии переполнения возможны четыре случая сочетания знаков и модулей слагаемых [11].

□ Случай 1.

Этот случай соответствует обычному сложению прямых кодов чисел:

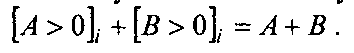
(Страница51)

□ Случай 2.

[A>0] _i +[B<0] _i =A+2+B - 2 ^{- n}. Назовем этот результат предварительным. Истинное значение результата в рассматриваемом случае (сумма положительна) будет A+B. Следовательно, предварительный результат нуждается в коррекции путем вычитания 2 и добавления 2 ^{- n}.

□ Случай 3.

[A>0] _i +[B<0] _i =A+2+B - 2 ^{- n}.Этот результат соответствует правильному, поскольку рассматривается случай отрицательной суммы.

□ Случай 4.

Здесь предварительный результат нуждается в коррекции путем вычитания 2 и добавления 2 ^{- n}, как и в случае 2, поскольку истинное значение отрицательной суммы, представленной в обратном коде, A+B+2-2^-n.

Заметим, что в случаях 2 и 4 требуется одинаковая коррекция: - 2+ 2 ^{- n}, причем только в этих двух случаях возникает перенос из знакового разряда. Действительно, в случае 4 оба знаковых разряда равны 1, а в случае 2 знак результата — 0, что при разных знаках слагаемых может получиться только при появлении переноса из первого разряда в нулевой (знаковый), а, следовательно, обязательно будет перенос и из знакового разряда. Вес знакового разряда соответствует 2⁰, а вес переноса из него — 2¹. Таким образом, игнорируя перенос из знакового разряда, мы вычитаем из результата 2, что соответствует первому члену корректирующего выражения. Для учета второго члена следует добавить 1 к младшему разряду суммы, вес которого составляет 2 ^{- n}.

В случаях 1 и 3 переноса из знакового разряда не возникает и коррекция результата не требуется.

Таким образом, для выполнения алгебраического сложения двоичных чисел, представленных в обратном коде, достаточно, не анализируя соотношение знаков и модулей, произвести сложение чисел, включая знаковые разряды, по правилам двоичной арифметики, причем возникающий в знаковом разряде перенос должен быть добавлен к младшему разряду результата, осуществляя ем самым коррекцию предварительной суммы. Полученный код является алгебраической суммой слагаемых, представленной в обратном коде.

Рассмотрим несколько примеров.

Пример 3.5

Сложить два числа в обратном коде. Результат — на рис. 3.4.

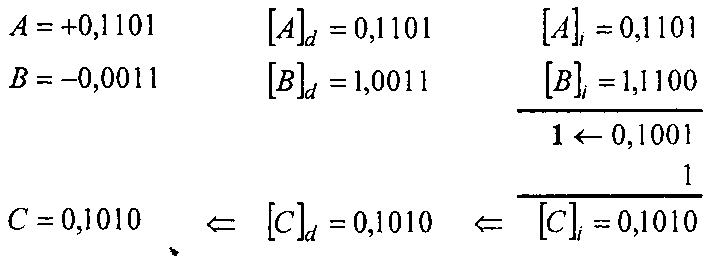
Рис. 3.4. Результат выполнения примера 3.5

Приведенный пример соответствует рассмотренному выше случаю 2; перенос, возникающий в знаковом разряде, циклически передается в младший разряд предварительного результата.

Пример 3.6

Сложить два числа в обратном коде (случай 3). Результат — на рис. 3.5.

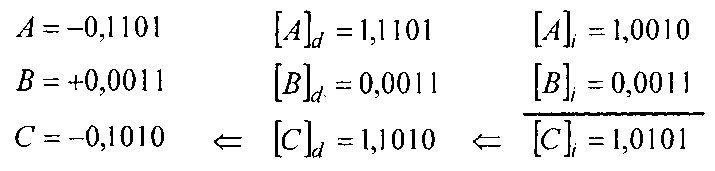
Рис. 3.5. Результат выполнения примера 3.6

Пример 3.7

Сложить два числа в обратном коде (случай 4). Результат — на рис. 3.6.

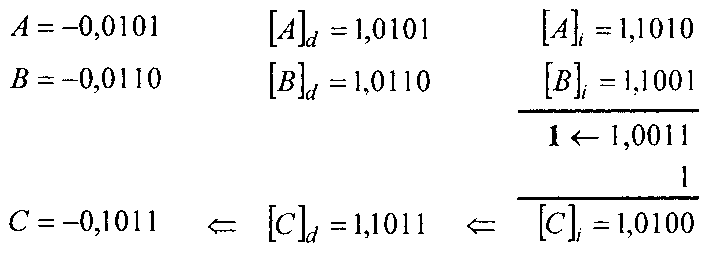
Рис. 3.6. Результат выполнения примера 3.7

Пример 3.8

Сложить два числа в обратном коде (одинаковые модули, но разные знаки). Результат — на рис. 3.7.

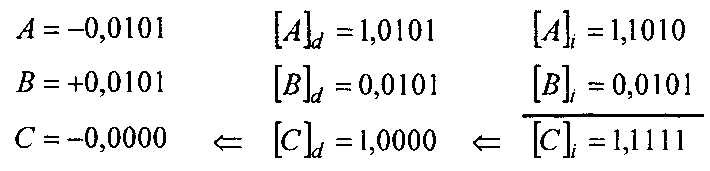
Рис. 3.7. Результат выполнения примера 3.8

Таким образом, ноль в обратном коде бывает "положительный" и "отрицательный" (обратите внимание на выражение (3.17)), причем добавление к числу "отрицательного" нуля, как и "положительного", дает в результате значение первого слагаемого.

Пример 3.9

Сложить два числа в обратном коде: 3+(-0). Результат — на рис. 3.8.

Рис. 3.8. Результат выполнения примера 3.9

Теперь рассмотрим случаи, когда что соответствует переполнению разрядной сетки. Очевидно, учитывая, что переполнение возможно только при сложении чисел с одинаковыми знаками. Рассмотрим примеры.

Пример 3.10

Сложить два числа в обратном коде: 13/16+5/16=18/16. Результат — на рис. 3.9.

Рис. 3.9. Результат выполнения примера 3.10

Пример 3.11

Сложить два числа в обратном коде: (-11/16)+(-8/16)=(-19/16). Результат — на рис. 3.10.

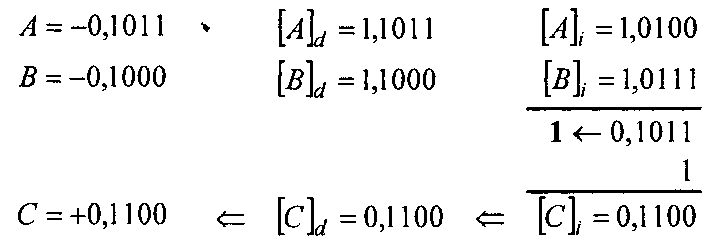
Рис. 3.10. Результат выполнения примера 3.11

Таким образом, признаком переполнения в обратном коде можно считать знак результата, противоположный одинаковым знакам слагаемых:

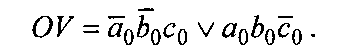(3.19)

Пример 3.12

Сложить числа в обратном коде (А>В, B>0, ). Результат — на рис. 3.11.

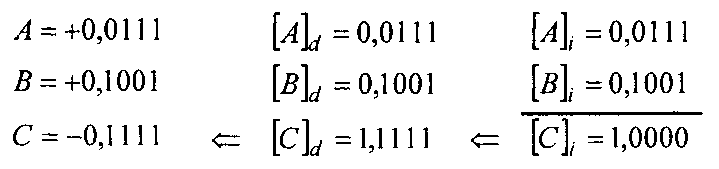
Рис. 3.11. Результат выполнения примера 3.12

Пример 3.13

Сложить числа в обратном коде 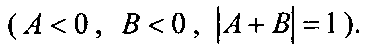Результат — на рис. 3.12.

Рис. 3.12. Результат выполнения примера 3.13

Переполнение в соответствии с (3.19) обнаруживается и в этих случаях.

Итак, использование обратного кода в операциях алгебраического сложения/вычитания позволяет:

□ использовать только действие арифметического сложения двоичных кодов;

□ получать истинное значение знака результата, выполняя над знаковыми разрядами операндов те же действия, что и над разрядами чисел;

□ обнаруживать переполнение разрядной сетки.

Еще одним достоинством применения обратного кода можно считать простоту взаимного преобразования прямого и обратного кода.

Однако использование обратного кода имеет один существенный недостаток — коррекция предварительной суммы требует добавления единицы к ее младшему разряду и может вызвать (в некоторых случаях) распространение переноса по всему числу, что, в свою очередь, приводит к увеличению вдвое времени суммирования. Для преодоления этого недостатка можно использовать вместо обратного дополнительный код.

Дата добавления: 2015-04-25