АЦП последовательного приближения

Когда необходимо разрешение 12, 14 или 16 разрядов и не требуется высокая скорость преобразования, а определяющими факторами являются невысокая цена и низкое энергопотребление, то обычно применяют АЦП последовательного приближения. Этот тип АЦП чаще всего используется в разнообразных измерительных приборах и в системах сбора данных. В настоящий момент АЦП последовательного приближения позволяют измерять напряжение с точностью до 16 разрядов с частотой дискретизации от 100К (1х10³) до 1М (1х10⁶) отсчетов/сек.

Рис. 6.10 показывает упрощенную блок-схему АЦП последовательного приближения. В основе АЦП данного типа лежит специальный регистр последовательного приближения. В начале цикла преобразования все выходы этого регистра устанавливаются в логический 0, за исключением первого (старшего) разряда. Это формирует на выходе внутреннего цифро-аналогового преобразователя (ЦАП) сигнал, значение которого равно половине входного диапазона АЦП. А выход компаратора переключается в состояние, определяющее разницу между сигналом на выходе ЦАП и измеряемым входным напряжением.

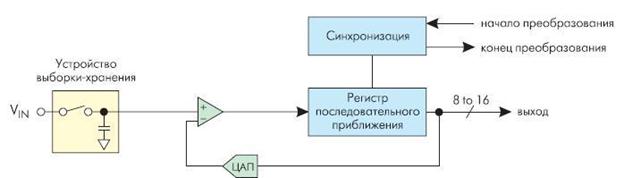
Рис. 6.10. АЦП последовательного приближения

Приближение к аналоговому сигналу происходит не “лесенкой”, т.е. начиная с младшего разряда, а скачками, сначала большими ступенями, так как заполнение регистра последовательного приближения начинается со старшего разряда кода, затем ступени уменьшаются в соответствии с “весом” разряда.

Дерево, иллюстрирующее работу 3-разрядного АЦП с регистром последовательных приближений, изображено на рис. 6.11.

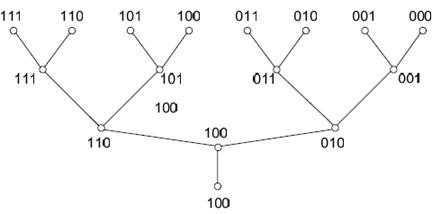
Рис. 6.11. Дерево аналого-цифрового преобразования

Движение по дереву влево от точки анализа сохраняет анализируемый разряд двоичного кода как единицу, вправо – требует его замену на нуль.

Например, для 8-разрядного АЦП последовательного приближения (рис. 6.12) выходы регистра при этом устанавливаются в "10000000". Если входное напряжение меньше половины входного диапазона АЦП, тогда выход компаратора примет значение логического 0. Это дает регистру последовательного приближения команду переключить свои выходы в состояние "01000000", что соответственно приведет к изменению выходного напряжения с ЦАП, подаваемого на компаратор. Если при этом выход компаратора по-прежнему оставался бы в "0", то выходы регистра переключились бы в состояние "00100000". Но на этом такте преобразования выходное напряжение ЦАП меньше, чем входное напряжение, и компаратор переключается в состояние логической 1 (рис. 6.12). Это предписывает регистру последовательного приближения сохранить "1" во втором разряде и подать "1" на третий разряд. Описанный алгоритм работы затем вновь повторяется до последнего разряда. Таким образом, АЦП последовательного приближения требуется один внутренний такт преобразования для каждого разряда, или N тактов для N-разрядного преобразования.

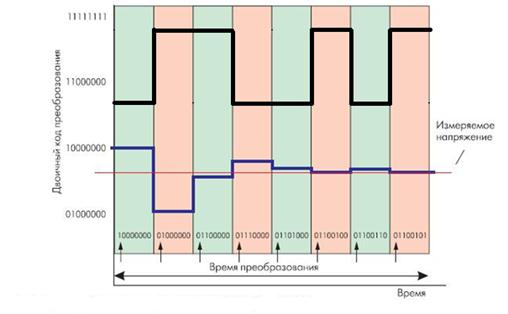
Рис. 6.12. Состояние компаратора и выходной код АЦП

Тем не менее, работа АЦП последовательного приближения имеет особенность, связанную с переходными процессами во внутреннем ЦАП. Теоретически, напряжение на выходе ЦАП для каждого из N внутренних тактов преобразования должно устанавливаться за одинаковый промежуток времени. Но на самом деле этот промежуток в первых тактах значительно больше, чем в последних. Поэтому время преобразования 16-разрядного АЦП последовательного приближения более, чем в два раза превышает время преобразования 8-разрядного АЦП данного типа.

АЦП последовательного приближения позволяют кратчайшим путем приблизиться к измеряемой величине и завершить процесс преобразования всего за m последовательных приближений (m-разрядность выходного кода) вместо 2 ^m-1 которые потребовались бы в случае использования метода одностороннего приближения. Выигрыш в быстродействии будет тем большим, чем разрядность m. При m=6 такой выигрыш будет более чем десятикратным (6 против 2⁶=64), то при m=10 он достигнет более двух порядков (10 против 2¹⁰=1024). С помощью таких АЦП в зависимости от числа используемых разрядов, можно получить до 10⁵ – 10⁶ преобразований в секунду. К тому же статическая погрешность преобразователей данного типа весьма незначительна и определяется в основном используемым ЦАП. Это позволяет реализовать разрешающую способность до 16 двоичных разрядов и более.

Данный класс АЦП, представляя собой разумный технический компромисс между точностью и быстродействием, находит широкое применение – как при построении цифровых измерительных приборов, так и в различных системах цифровой обработки быстро меняющихся сигналов совместно с УВХ или без последних.

Дата добавления: 2015-03-29