Собственные частоты колебаний пластинчатых конструкций

При расчете пластин (рис. 8) обычно принимают следующие допущения:

1) изгибные деформации пластины при колебаниях малы по сравнению с ее толщиной, упругие деформации подчиняются закону Гука;

2) пластина имеет постоянную толщину;

3) материал пластины идеально упругий, однородный и изотропный.

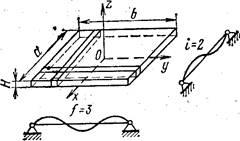Рисунок 8 – Пластина и возможные формы ее колебаний

При составлении уравнений движения используют уравнение изгиба пластины при действии распределенной статической нагрузки q (x, y) [7]

, (16)

где w = w (x, y) – прогиб пластины в точке с координатами x и y;

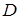– жесткость пластины на изгиб (цилиндрическая жесткость), равная

, (17)

где Е и – соответственно модуль упругости и коэффициент Пуассона материала пластины;

– толщина пластины.

При расчете динамических характеристик ячеек РЭА их представляют в виде пластин с жестко защемленными или шарнирно закрепленными краями. На рис. 9 приведены модели ячеек с использованием схемы жесткого защемления (рис. 9, а) или шарнирного опирания (рис. 9, б). Масса ЭРЭ принимается равномерно распределеной по всей площади пластины, а жесткость модели принимается равной жесткости платы [8].

Рисунок 9 – Модели ячейки:

1- свободный край; 2 – жестко защемленный край; 3 – свободно опертый край

Частота собственных колебаний равномерно нагруженной пластины может быть представлена в виде

f₀ = (18)

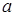где и 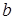– длинная сторона и короткая сторона пластины; М – масса пластины с ЭРЭ; 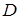– цилиндрическая жесткость пластины, определяемая по формуле (17); 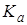– коэффициент, зависящий от способа закрепления сторон пластины, определяется по общей формуле

K_a = , (19)

где k, α, β, γ — коэффициенты, соответствующие заданному способу закрепления сторон ПП.

Значения коэффициентов k, α, β, γ для некоторых из возможных вариантов крепления пластин приведены в таблице 1[1].

Таблица 1 – Закрепление плат

№	Варианты крепления пластин	Коэффициенты
k	α	β	γ
		9,87
		9,87		2,33	2,44
		15,42		0,95	0,41
		9,87		2,57	5,14
		15,42		1,11
		22,37		0,57	0,47
		15,42		1,19	2,1

— сторона пластины защемлена;

— сторона пластины лежит на опоре (в направляющей).

В качестве пластины могут выступать кассеты, платы, стенки блоков и т.п. Если прогиб и угол поворота на краю пластины равны нулю, то этот край считают жестко защемленным (закрепленным). Жестко закрепление края пластин осуществляется пайкой, сваркой, зажимом, винтовым соединением. Закрепленным краем пластины можно считать сторону, вставленную в разъем. Если прогиб и изгибающий моменты равны нулю, то этот край опертый. Шарнирно закрепленная сторона – сторона пластины, находящаяся в направляющей, гнездовой соединитель.

В РЭА часто используются платы, закрепленные в отдельных точках. Если плата крепится на колонках винтами, то такому креплению наиболее точно соответствует схема свободного опирания в этих точках.

Для пластины, закрепленной в четырех точках, определить первую собственных частоту колебаний можно по формуле:

f₀ = .

При других способах крепления формулы для определения собственной частоты колебаний приведены в [9].

Дата добавления: 2015-04-25