
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия и определения. Список цитируемых источников
|
|
|
|
Теория
Механические КОЛЕБАния
Лабораторная работа 1-3
Список цитируемых источников
Характеристики некоторых упаковочных материалов
| Наименование материала | Плотность, ρ ·103, кг·м-3 | Предельное допускаемое давление, σ д·104, Па | Относительный коэффициент демпфирования, δ 0 |
| Полиуретановый пенопласт (поролон) | 0,03... 0,07 | 0,8... 1,0 | - |
| Резина губчатая | 0,127 | 3,0 | 0,12 |
| Упругий полиуретан замкнутой структуры | 0,35 | 20,0 | 0,08 |
| Пробка натуральная | - | 15,0... 20,0 | 0,127 |
| Войлок мягкий | - | 2,0... 3,0 | 0,18... 0,20 |
| Сетчатые цельно-металлические листы из проволоки ЭИ708 диаметром 0,09 | 1,0 1,87 2,68 | 20,0 30,0 140,0 | 0,3... 0,4 0,3... 0,4 0,3... 0,4 |
1. Парфенов Е.М., Камышная Э.Н., Усачев В.П. Проектирование конструкций радиоэлектронной аппаратуры. М.: Радио и связь, 1989.
2. Карпушин В. Б. Виброшумы радиоаппаратуры. –М.: Сов. Радио, 1977. –318 с.
3. Абжирко Н.Н. Влияние вибрации на характеристики электронных антенн. –
М.: Сов. Радио, 1974. –168 с.
4. Ковалев Н.А. Прикладная механика. Учебник для вузов. – М.,: Высш. шк., 1972.-400 с.
5. Феодосьев В. И. Сопротивление материалов. –М.: Наука, 1974. –560 с.
6. Вибрации в технике: Справочник в 6-ти т. – Т. 1/Под ред. В.В.Болотина. – М.: Машиностроение. 1978. – 352 с.
7. Филлипов А.П. Колебания деформируемых систем. – М.: Машиностроение, 1970. –736 с.
8. Фролов В.А. Механические воздействия и защита электронной аппаратуры. – К.: Высш. шк., 1979. – 128 с.
9. Справочник конструктора РЭА / Под Ред. Р.Г.Варламова. – М.: Сов. Радио, 1980. – 480 с.
Цель работы: изучение основных закономерностей колебательного движения.
Колебательным движением называется, движение, обладающее той или иной степенью повторяемости во времени.
Простейшими колебаниями являются гармонические колебания, т. е. такие колебания, при которых колеблющаяся величина (колебания маятника, поршня и т. п.) изменяется со временем по закону синуса или косинуса. Уравнение гармонического колебания следующее:
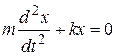 или
или 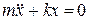 ,
, 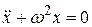 (1)
(1)
где  — коэффициент упругости, m — масса колеблющейся системы, х — смещение колеблющейся системы, F = — kx — возвращающая или центральная сила. Решение такого уравнения имеет вид:
— коэффициент упругости, m — масса колеблющейся системы, х — смещение колеблющейся системы, F = — kx — возвращающая или центральная сила. Решение такого уравнения имеет вид:
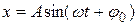 или
или 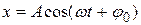 (2)
(2)
где х — колеблющаяся величина (смещение, скорость, ускорение, сила и т. п.), t — время, А — амплитуда колебания, равная максимальному абсолютному значению х (максимальное отклонение колеблющейся величины от положения равновесия), w — циклическая или круговая частота (рис. 1).
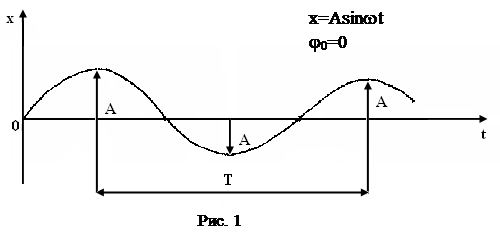 Физический смысл циклической частоты состоит в том, что w численно равна числу полных колебаний, совершаемых за 2p сек, т. е.
Физический смысл циклической частоты состоит в том, что w численно равна числу полных колебаний, совершаемых за 2p сек, т. е. 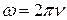 ,
,  , где
, где  — частота колебаний, т. е. число полных колебаний, совершаемых за единицу времени; Т — период колебаний — время, за которое совершается одно полное колебание,
— частота колебаний, т. е. число полных колебаний, совершаемых за единицу времени; Т — период колебаний — время, за которое совершается одно полное колебание, 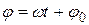 — фаза колебания. Фаза колебания - функция времени определяет значение х в данный момент времени t,
— фаза колебания. Фаза колебания - функция времени определяет значение х в данный момент времени t, 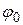 — начальная фаза колебания в момент начала отсчета времени, т. е. при t = 0.
— начальная фаза колебания в момент начала отсчета времени, т. е. при t = 0.
 Если в уравнение (1) подставить одно из решений (2), то получим:
Если в уравнение (1) подставить одно из решений (2), то получим:
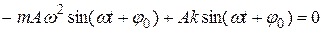
Отсюда  (3)
(3)
Формула (1) описывает гармоническое колебательное движение, происходящее вдоль какой-либо линии, такие колебания называются колебательными системами с одной степенью свободы (рис. 2 а). Если система может совершать два независимых друг от друга колебания в двух взаимно перпендикулярных направлениях, то такая система обладает двумя степенями свободы (рис. 2, б).
Пружинный маятник может колебаться в трех независимых направлениях и называется колебательной системой с тремя степенями свободы (рис. 2, в). Если система совершает колебания около положения равновесия (после того как она каким-либо образом была выведена из положения устойчивого равновесия) без воздействия переменных внешних сил, то такие колебания называются собственными или свободными. Частота, с которой колеблется система ( ) - при свободных колебаниях, называется собственной частотой системы.
) - при свободных колебаниях, называется собственной частотой системы.
1. Рассмотрим некоторые примеры свободных незатухающих колебаний тел, т. е. колебаний с неизменной амплитудой.
- Колебания груза на пружине. Колебательное движение происходит под действием упругой или квазиупругой силы F (силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие уравнению F=-kx, называются квазиупругими):
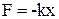
Эта сила всегда направлена к положению равновесия, а смещение х — в противоположную сторону, поэтому имеем знак минус. Такая сила называется возвращающей силой. По второму закону Ньютона
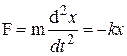 или
или  (4)
(4)
где m – масса колеблющегося тела, k – коэффициент упругости;
 (5)
(5)
 где
где  - частота;
- частота;  - период собственных колебаний.
- период собственных колебаний.
Из формулы (5) легко определить период собственных упругих колебаний, например, груза на пружине. Так как
 , то (6)
, то (6)
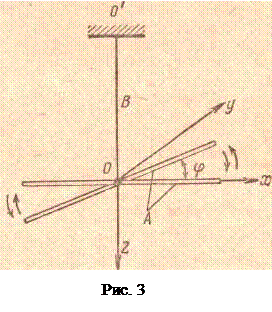
- Крутильные колебания. Система совершает крутильные колебания, т. е. такие колебания, при которых твердое тело А, подвешенное на вертикальной невесомой нити (или невесомом стержне В), верхний конец которой закреплен неподвижно в точке О', а ось z совпадает с одной из свободных осей тела, колеблется в плоскости хОу, отклоняясь от оси х на угол  вправо и влево (рис. 3).
вправо и влево (рис. 3).
При крутильных колебаниях на тело действует возвращающий момент, приостанавливающий отклонение тела от состояния равновесия, а затем сообщающий телу обратное движение.
Возвращающий момент М обусловлен упругими силами, возникающими в стержне при его кручении вокруг оси Oz.
В случае малых углов  крутильные колебания можно считать гармоническими и тогда по второму закону механики для вращательного движения
крутильные колебания можно считать гармоническими и тогда по второму закону механики для вращательного движения
 ,
,  ,
, 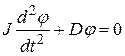 ;
;  (7)
(7)
где D — постоянная величина для данного стержня (нити), называется, модулем кручения, a  (см. формулу (4)). Из формулы (6) период собственных крутильных колебаний
(см. формулу (4)). Из формулы (6) период собственных крутильных колебаний
 (8)
(8)
где J — момент инерции тела А относительно оси Оz.
-  М а я т н и к. 1) Точечное тело, подвешенное к невесомой и нерастяжимой нити, совершающее колебания в вертикальной плоскости под действием собственного веса, называется математическим маятником (рис. 4, а).
М а я т н и к. 1) Точечное тело, подвешенное к невесомой и нерастяжимой нити, совершающее колебания в вертикальной плоскости под действием собственного веса, называется математическим маятником (рис. 4, а).
В вертикальном положении сила тяжести материальной точки  полностью уравновешивается натяжением нити
полностью уравновешивается натяжением нити  и маятник остается в покое (положение равновесия — точка А). Если маятник отклонить от положения равновесия в точку С на некоторый угол
и маятник остается в покое (положение равновесия — точка А). Если маятник отклонить от положения равновесия в точку С на некоторый угол  , то составляющая силы тяжести, направленная вдоль нити, т.е. сила
, то составляющая силы тяжести, направленная вдоль нити, т.е. сила  уравновесится натяжением нити
уравновесится натяжением нити 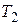 , другая же составляющая, т.е. сила
, другая же составляющая, т.е. сила  , перпендикулярная к нити, стремится вернуть маятник в положение равновесия. Эта сила является возвращающей силой. В этом случае движение маятника определяется не упругой силой, а квазиупругой силой. Квазиупругая сила
, перпендикулярная к нити, стремится вернуть маятник в положение равновесия. Эта сила является возвращающей силой. В этом случае движение маятника определяется не упругой силой, а квазиупругой силой. Квазиупругая сила 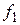 — сила, не упругая по своей природе, но аналогичная упругой силе по виду зависимости от смещения. Колебания, вызываемые этой силой при малых углах
— сила, не упругая по своей природе, но аналогичная упругой силе по виду зависимости от смещения. Колебания, вызываемые этой силой при малых углах  , совпадают по характеру движения с колебаниями, вызываемыми упругой силой.
, совпадают по характеру движения с колебаниями, вызываемыми упругой силой.
Длина дуги х = АС, на которую маятник отклонился от положения равновесия, называется смещением. Если смещение от А к С считать положительным, а от А к В — отрицательным, то сила 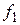 всегда будет направлена обратно смещению и при малых углах отклонения (2—4°) пропорциональна смещению.
всегда будет направлена обратно смещению и при малых углах отклонения (2—4°) пропорциональна смещению.
При отклонении маятника на угол  на точку С действует вращающий момент
на точку С действует вращающий момент
 ;
;  (9)
(9)
где l — плечо силы 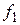 . Маятник будет совершать движение по окружности около точки подвеса О. По второму закону динамики для вращательного движения
. Маятник будет совершать движение по окружности около точки подвеса О. По второму закону динамики для вращательного движения
 (10)
(10)
где 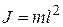 — момент инерции точки. Приравнивая формулы (9) и (10), получим:
— момент инерции точки. Приравнивая формулы (9) и (10), получим:
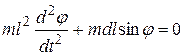 или
или 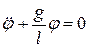 (11)
(11)
(для малых углов  , если
, если  измерять в радианах и
измерять в радианах и  ). Это уравнение такое же, как и уравнение (4), поэтому можно заменить
). Это уравнение такое же, как и уравнение (4), поэтому можно заменить 
и период свободных колебаний математического маятника
 (12)
(12)
где l — длина математического маятника.
2) Если вместо точки возьмем твердое тело, совершающее колебания под действием собственного веса Р вокруг неподвижной оси О, не проходящей через центр тяжести тела С, то будем иметь физический маятник (рис. 4, б). На рисунке точка О — точка подвеса, С — центр тяжести. При отклонении маятника на угол  составляющая веса Р сила f2 уравновешивается реакцией оси О. Составляющая же f1 стремится возвратить маятник в положение равновесия. Для малых углов
составляющая веса Р сила f2 уравновешивается реакцией оси О. Составляющая же f1 стремится возвратить маятник в положение равновесия. Для малых углов
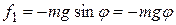
Возвращающий момент М, создаваемый силой f1 численно равен:
 (13)
(13)
где L = ОС плечо силы f1.
По второму закону динамики для вращательного движения
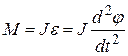 (14)
(14)
где J — момент инерции маятника относительно оси О. Из формул (13) и (14) имеем:
 ;
;  (15)
(15)
Уравнение (15) аналогично уравнениям (4), (7) и (11), поэтому 
Отсюда период собственных колебаний физического маятника
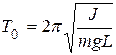 (16)
(16)
Выражение  называется приведенной длиной физического
называется приведенной длиной физического
маятника.
Приведенной длиной физического маятника называется длина некоторого воображаемого математического маятника, которой имеет тот же период колебаний, что и данный физический маятник.
На практике приведенная длина физического маятника определяется расстоянием между точкой подвеса маятника О и его центром качания О' (точкой, находящейся от точки подвеса на расстоянии, равном приведенной длине маятника). Центр качания лежит ниже центра тяжести маятника. Маятник, вся масса которого была бы сосредоточена в центре качания, имел бы тот же период, что и математический маятник данной длины.
2. Если колеблющаяся система находится в вязкой среде, то колебания через некоторое время прекратятся. Это явление представляет собой затухающее колебание.
Затухающими колебаниями называются колебания, энергия которых уменьшается с течением времени.
Система тел, механическая энергия которых постепенно уменьшается за счет преобразования в другие виды энергии, называется диссипативной. Все реальные колебательные системы являются диссипативными. Энергия в диссипативной системе расходуется на работу против сил трения. Затухающие колебания совершаются при одновременном действии двух сил: упругой силы и силы сопротивления среды. Уравнение затухающего колебания при небольших затуханиях имеет вид:
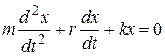 или
или  или
или  (17)
(17)
где m — масса колеблющегося тела, а — его ускорение, -kx — упругая (возвращающая) сила, Fтр= -rv — сила сопротивления среды — сила трения, r — коэффициент сопротивления среды, v — скорость движения тела в среде. Решение уравнения (17) дает зависимость смещения х от времени t: 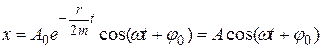 , где
, где 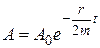 - амплитуда затухающих колебаний, е – основание натурального логарифма,
- амплитуда затухающих колебаний, е – основание натурального логарифма, 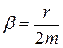 коэффициент затухания,
коэффициент затухания, 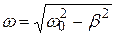 собственная циклическая частота затухающих колебаний системы,
собственная циклическая частота затухающих колебаний системы,  — собственная циклическая частота свободных колебаний системы (в отсутствие вязкой среды).
— собственная циклическая частота свободных колебаний системы (в отсутствие вязкой среды).
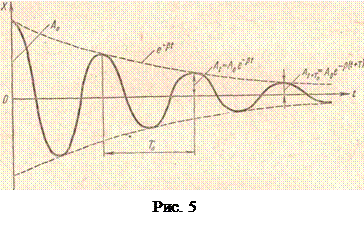 Затухающее колебание при
Затухающее колебание при  показано на рис. 5.
показано на рис. 5.
Отношение двух последующих амплитуд одного и того же знака At и At+T, отстоящих друг от друга на период Т, равно:
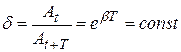 (18)
(18)
и называется декрементом затухания.
Натуральный логарифм от этого отношения
 (19)
(19)
называется логарифмическим декрементом затухания.
3. Если на систему действует периодическая сила, поддерживающая колебание системы, то система совершает вынужденные незатухающие колебания.
Уравнение вынужденных прямолинейных колебаний имеет вид:
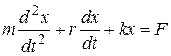 или
или  или
или 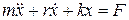 (20)
(20)
где F — периодически действующая внешняя сила, вынуждающая или возмущающая,  , где F0 — амплитуда вынуждающей силы.
, где F0 — амплитуда вынуждающей силы.
экспериментальная часть
задача 1. Определение ускорения силы тяжести при помощи математического маятника.
Приборы и принадлежности: маятник, секундомер. При выполнении эксперимента с помощью Interactive Physics рабочий файл – «Lab 1-3-mm.ip».
 В эксперименте исследуется колебательное движение груза, подвешенного на длинной нити. Соотношение его элементов таково, что этот физический маятник с достаточной степенью точности может считаться моделью математического маятника.
В эксперименте исследуется колебательное движение груза, подвешенного на длинной нити. Соотношение его элементов таково, что этот физический маятник с достаточной степенью точности может считаться моделью математического маятника.
Математический маятник (рис. 6), применяемый в эксперименте, представляет собой массивный шарик небольшого радиуса, подвешенный на двойной нити для того, чтобы колебания происходили строго в одной плоскости.
Ускорение свободного падения с учётом выражения (10) можно определить по формуле:
 (21)
(21)
где 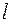 - длина математического маятника, которую можно считать равной расстоянию от точки подвеса до центра шарика;
- длина математического маятника, которую можно считать равной расстоянию от точки подвеса до центра шарика;  - период колебаний.
- период колебаний.
Однако, расчёт 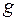 по формуле (21) является неточным, ввиду того, что допускаются погрешности при определении длины маятника. Поэтому поступают следующим образом: измеряют длину маятника
по формуле (21) является неточным, ввиду того, что допускаются погрешности при определении длины маятника. Поэтому поступают следующим образом: измеряют длину маятника 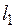 и определяют период
и определяют период  по формуле (12), затем изменяют длину до значения
по формуле (12), затем изменяют длину до значения  и определяют соответствующий период
и определяют соответствующий период 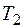 . Разность квадратов периодов равна:
. Разность квадратов периодов равна:  ,
,
откуда:
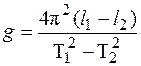 (22)
(22)
Таким образом, при расчёте ускорения свободного падения по формуле (22) исключаются систематические погрешности, возникающие при измерении длины математического маятника в данной установке. Учёт случайных погрешностей осуществляется статистическим методом.
1. Замерить длину нити маятника 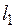 .
.
2. Ввести маятник в движение, отклонив шарик на 4-50 от положения равновесия.
3. Измерить время, за которое маятник совершит 10 полных колебаний.
4. По формуле (12) определить период  математического маятника.
математического маятника.
5. Изменить длину маятника, повторить всю последовательность операций, рассчитать новый период колебаний 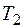 .
.
6. По формуле (22) определить ускорение свободного падения.
7. Опыт повторить не менее 3-х раз. Выполнить статистическую проверку по методу Стьюдента. Сравнить полученное значение «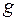 » с табличным.
» с табличным.
задача 2. Изучение собственных колебаний пружинного маятника.
Приборы и принадлежности: набор пружин и грузов, штатив, секундомер, сосуд с вязкой жидкостью.
Теория метода и описание установки. В данной работе рассматривают простейший случай собственных незатухающих колебаний пружинного маятника, а именно колебания груза на пружине. В воздухе эти колебания можно считать незатухающими. Уравнение таких колебаний имеет вид
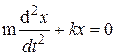 или
или 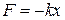 (23)
(23)
где k — коэффициент упругости пружины.
Коэффициент k можно определить опытным путем, если измерить величину х, на которую растянется пружина А при подвешивании к ней груза Р=F (рис. 7, а):
 (24)
(24)
Измерения и обработка результатов измерений.
Определение коэффициента упругости.
1. Находят коэффициент упругости для каждой пружины по формуле (24). Измерения проводят для каждой пружины при трех различных грузах Р. При выполнении эксперимента с помощью Interactive Physics рабочий файл – «Lab 1-3-pr-1.ip».
2.  Определяют зависимость периода собственных колебаний пружинного маятника от массы груза. Для этого измеряют секундомером период Ti собственных колебаний для одной из пружин с коэффициентом упругости k1 при разных грузах Р и строят график зависимости
Определяют зависимость периода собственных колебаний пружинного маятника от массы груза. Для этого измеряют секундомером период Ti собственных колебаний для одной из пружин с коэффициентом упругости k1 при разных грузах Р и строят график зависимости 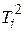 от m (по оси х откладывают массу m).
от m (по оси х откладывают массу m).
Период Тi измеряют из 10—15 полных колебаний
 ,
,
где ti - время ni полных колебаний.
3. Находят зависимость собственных колебаний маятника от коэффициента упругости пружины, для чего измеряют периоды Т0 собственных колебаний пружин при одном и том же грузе Р0 и строят график зависимости Т0 от k (по оси абсцисс  откладывают значения k). При выполнении эксперимента с помощью Interactive Physics рабочий файл – «Lab 1-3-pr-2.ip».
откладывают значения k). При выполнении эксперимента с помощью Interactive Physics рабочий файл – «Lab 1-3-pr-2.ip».
4. По формуле (6) вычисляют теоретически коэффициенты упругости пружин используя значения Т0, полученные опытным путем. Вычисленные значения k0 сравнивают с опытными результатами, полученными по формуле (24) для одних и тех же грузов Р.
Результаты измерений и вычислений записывают в таблицы для короткой пружины № 1, средней № 2 и длинной № 3 (рис. 8).
| № пружин | P0= | |||||||||
| № опыта | P | x | 
| ti | ni | 
| 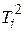
| 
| 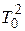
| 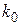
|
| … | ||||||||||
| Среднее значение | ´ | ´ | ´ | ´ | ´ | ´ | ´ | ´ |
Определение логарифмического декремента затухания пружинного маятника методом сравнения амплитуд.
1. Один из грузов Р помещают в сосуд с вязкой жидкостью (рис. 7, б) и приводят в колебание. Измеряют время  , за которое начальная амплитуда А0 уменьшится в 10 раз, т. е. At=10A0. Первоначальную амплитуду берут равной 70—100 мм. При выполнении эксперимента с помощью Interactive Physics рабочий файл – «Lab 1-3-pr-3.ip».
, за которое начальная амплитуда А0 уменьшится в 10 раз, т. е. At=10A0. Первоначальную амплитуду берут равной 70—100 мм. При выполнении эксперимента с помощью Interactive Physics рабочий файл – «Lab 1-3-pr-3.ip».
Вычисляют логарифмический декремент затухания l, для этого формулу (19) преобразуют следующим образом. Время t берут не для одного периода, а для n периодов и вычисляют отношение d двух амплитуд для времени t = 0 и t=t0+nT0, т.е. 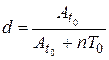 , где Т0 — период затухающих колебаний.
, где Т0 — период затухающих колебаний.
В это выражение подставляют значения
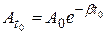 и
и 
и получают:

После логарифмирования будем иметь:

Отсюда
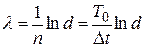 (25)
(25)
где  — время, за которое маятник совершил n полных колебаний, т. е.
— время, за которое маятник совершил n полных колебаний, т. е.  , d — отношение двух амплитуд, отличающихся друг от друга на время
, d — отношение двух амплитуд, отличающихся друг от друга на время  . В нашем случае d = 10 (амплитуда уменьшилась в 10 раз) и окончательная формула для l пружинного маятника будет:
. В нашем случае d = 10 (амплитуда уменьшилась в 10 раз) и окончательная формула для l пружинного маятника будет:
 (26)
(26)
По этой формуле вычисляют l не менее трех раз, меняя начальную амплитуду А0. Значения Т0 берут из первого упражнения для той пружины, с которой проводили данное измерение.
2. Из формул 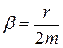 и (19) вычисляют коэффициент сопротивления (трения) среды:
и (19) вычисляют коэффициент сопротивления (трения) среды: 
Измерения и результаты вычислений записывают в таблицу.
| A0 | 
| l | r | Т0= m= |

| ´ | |||
| Среднее значение | ´ | ´ | ||
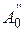
| ´ | |||
| Среднее значение | ´ | ´ | ||

| ´ | |||
| Среднее значение | ´ | ´ |
Контрольные вопросы
1. Запишите закон движения гармонически колеблющегося тела?
2. Напишите дифференциальное уравнение гармонических колебаний?
3. Что представляют собой свободные и вынужденные незатухающие колебания?
4. Какими выражениями определяются периоды колебаний физического, математического и пружинного маятников?
5. Какие силы называют квазиупругими?
6. Затухающие колебания. Уравнение затухающих колебаний.
7. Как зависит ускорение свободного падения от высоты и географической широты местности?
8. Поясните метод сравнения амплитуд использующийся для определения логарифмического декремента затухания пружинного маятника.
литература
1. Матвеев А.Н. Механика и теория относительности. М., 1986. 181 с.
2. Сивухин Д.В. Общий курс физики: Механика. М., 1989. 225 с.
3. Савельев И.В. Курс общей физики. М., 1987.
4. Майсова Н.Н. Практикум по курсу общей физики. М., 1979.
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами.
Все системы счисления делятся на позиционные и непозиционные.
Непозиционными системами являются такие системы счисления, в которых каждый символ сохраняет свое значение независимо от места его положения в числе.
Примером непозиционной системы счисления является римская система. К недостаткам таких систем относятся наличие большого количества знаков и сложность выполнения арифметических операций.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, определяющееся позицией цифры в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции, занимаемой цифрой, по некоторому закону.
Примером позиционной системы счисления является десятичная система, используемая в повседневной жизни.
Количество p различных цифр, употребляемых в позиционной системе определяет название системы счисления и называется основанием системы счисления - "p".
В десятичной системе используются десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9; эта система имеет основанием число десять.
Любое число N в позиционной системе счисления с основанием p может быть представлено в виде полинома от основания p:
N = anpn+an-1pn-1+... +a1p+a0+a-1p-1+a-2p-2+...
здесь N - число, aj - коэффициенты (цифры числа), p - основание системы счисления (p>1).
Принято представлять числа в виде последовательности цифр:
N = anan-1... a1a0. a-1a-2...
В этой последовательности точка отделяет целую часть числа от дробной (коэффициенты при положительных степенях, включая нуль, от коэффициентов при отрицательных степенях). Точка опускается, если нет отрицательных степеней (число целое).
В ЭВМ применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную.
В аппаратной основе ЭВМ лежат двухпозиционные элементы, которые могут находиться только в двух состояниях; одно из них обозначается 0, а другое - 1. Поэтому основной системой счисления применяемой в ЭВМ является двоичная система.
Двоичная система счисления. Используется две цифры: 0 и 1. В двоичной системе любое число может быть представлено в виде:
N = bnbn-1... b1b0. b-1b-2...
где bj либо 0, либо 1.
Восьмеричная система счисления. Используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Употребляется в ЭВМ как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используется три двоичных разряда (триада) (Таблица 1).
Шестнадцатеричная система счисления. Для изображения чисел употребляются 16 цифр. Первые десять цифр этой системы обозначаются цифрами от 0 до 9, а старшие шесть цифр - латинскими буквами: 10-A, 11-B, 12-C, 13-D, 14-E, 15-F. Шестнадцатеричная система используется для записи информации в сокращенном виде. Для представления одной цифры шестнадцатеричной системы счисления используется четыре двоичных разряда (тетрада) (Таблица 1).
Таблица 1. Наиболее важные системы счисления.
| Двоичная (Основание 2) | Восьмеричная (Основание 8) | Десятичная (Основание 10) | Шестнадцатиричная (Основание 16) | ||
| триады | тетрады | ||||
| 0 1 | 0 1 2 3 4 5 6 7 | 000 001 010 011 100 101 110 111 | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
1.2 Перевод чисел из одной системы счисления в другую.
Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.
Пример.
а) Перевести 10101101.1012  "10" с.с.
"10" с.с.
|
|
|
|
Дата добавления: 2015-04-25; Просмотров: 520; Нарушение авторских прав?; Мы поможем в написании вашей работы!