Endfunction

Вопрос № 11

Поиск минимума функции y=f(x) на интервале [ a, b]

Функция [f1,xopt]=optim(costf,x0) возвращает локальный минимум функции costf.

Функция возвращает минимум функции (значение f1) и точку, в которой этот минимум достигается (xopt).

Главной особенностью функции optim является структура функции costf, которая должна быть такой:

function [f,g,ind]=costf(x,ind)

f=gg(x);//функция, минимум которой мы ищем

g=numdiff(gg,x); //градиент функции f

Если возвращаемое сформированной функцией costf значение ind равно 2, 3 или 4, то функция costf обеспечивает поиск минимума, т.е. в качестве результата функции optim возвращается f и xopt. Если ind=1, то в функции optim ничего не считается, условие ind<0 означает, что минимум f(x) не может быть оценен, а ind=0 прерывает оптимизацию. Вообще говоря, значение параметра ind является внутренним параметром для связи между optim и costf, для использования optim необходимо помнить, что параметр ind должен быть определен в функции costf.

Пример: найти минимум функции .

Решение. Построим график функции для определения интервалов [ a, b], на которых находятся экстремумы этой функции.

-->x=-3:.1:3; y=x.^4-3*x.^2-5*x-4; plot(x, y); xgrid()

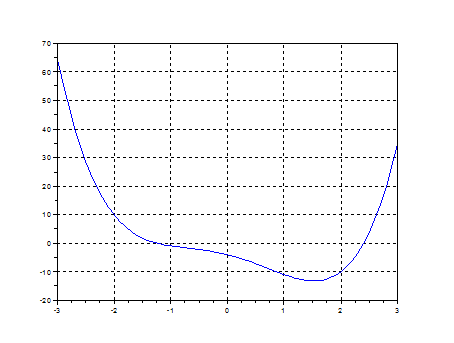
Из графика видно, что это отрезок [1, 2]. Набираем в окне редактора и отправляем на выполнение файл

function [f,g,r]=z(x,r)

f=x.^4-3*x.^2-5*x-4

g=4*x.^3-6*x-5

endfunction

x0=1;

[fmin,xmin]=optim(z,x0)

Получаем

--> xmin =

1.5233402

fmin =

- 13.193373

Возможен другой вариант, без ручного вычисления производной:

function y=gg(x)

y=x.^4-3*x.^2-5*x-4;

endfunction

function [f,g,r]=z(x,r)

f=gg(x)

g=numdiff(gg,x)

endfunction

x0=1;

[fmin,xmin]=optim(z,x0)

xmin =

1.5233402

fmin =

- 13.193373

В случае функции двух переменных:

(Поиск минимума функции Розенброка )

clc

x0=[-2;2];

function y=gg(x)

y=100*(x(2)-x(1)^2)^2+(1-x(1))^2;

endfunction

function [f,g,r]=z(x,r)

f=gg(x)

g=numdiff(gg,x)

endfunction

[fmin,xmin]=optim(z,x0)

xmin =

0.9999955

0.9999910

fmin =

2.010D-11

Дата добавления: 2015-03-29