Закон Ома для цепи с индуктивностью может быть применим только для амплитудных и действующих значений тока и напряжения и не может применяться для мгновенных напряжений, т.к. и

С уве­личением частоты тока индуктивное сопротивление X_L увеличивается (рис. 25). Физически это объясня­ется тем, что возрастает скорость изменения тока, а следовательно, и ЭДС самоиндукции.

Рис. 25

Мгновенная мощность. Как и для цепи с R, мгно­венное значение мощности определяется произведе­нием мгновенных значений напряжения и тока:

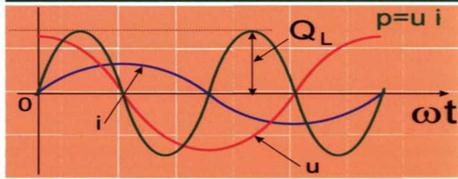
Рис. 26. Ток, напряжение и мощность цепи с индуктивностью L

Из графика на рис. 26 видно, что при одинаковых знаках напряжения и тока мгновенная мощность по­ложительна, а при разных знаках – отрицательна. Физически это означает, что в первую четверть периода переменного тока энергия источника преобразуется в энергию магнитного поля катушки. Во вторую чет­верть периода, когда ток убывает, катушка возвра­щает накопленную энергию источнику. В следующую четверть периода процесс передачи энергии источни­ком повторяется и т. д. Мощность изменяется с двойной частотой. Таким образом, в среднем катушка не потребляет энергии и, следовательно, активная мощность Р=0.

Реактивная мощность х арак­теризует интенсивности обмена энергией между источником и катушкой:

Единица реактивной мощности – вольт-ампер реактивный (Вар).

19.Электрические цепь с ёмкостью: законы изменения тока, напряжения, мощно­сти.

Рассмотрим электрическую цепь, в которой переменное напряжение u(t) = U_m∙sinωt приложено к ёмкости.

Рис.4.19. Цепь с ёмкостью.

Мгновенное значение тока в цепи с ёмкостью равно скорости изменения заряда на обкладках

конденсатора i = , но q = C∙u, то

I = C∙ = ω∙C∙U_m∙cosωt = I_m∙sin(ωt + π/2), где

ω∙C∙U_m = I_m.

Мы видим, что в этой цепи ток опережает напряжение на угол π/2. Перейдя к действующим значениям переменного тока I = I_m / √2, U = U_m / √2, получим:

I = U / X_c.

Это закон Ома для цепи переменного тока с ёмкостью, а величина X_c = 1 / ω∙C называется емкостным сопротивлением. Векторная диаграмма для этой цепи:

Рис.4.20. Векторная диаграмма цепи с ёмкостью.

Здесь ток опережает напряжение на π/2.

Посмотрим, что будет представлять собой мгновенная мощность в цепи, содержащей ёмкость.

p(t) = I_m∙U_m∙sinωt∙sin(ωt + π/2) = I_m∙U_m∙sin2ωt.

Временная диаграмма показана ниже.

Рис.4.21.Временная диаграмма изменения мгновенной мощности в цепи с индуктивностью.

Мы видим, что мгновенная мощность изменяется с удвоенной частотой. При этом положительные значения мощности соответствуют заряду конденсатора, а отрицательные - возврату запасённой энергии в источник. Средняя за период мощность здесь равна нулю, поскольку в цепи с конденсатором активная мощность не потребляется, а происходит обмен электрической энергии между конденсатором и источником. Следовательно, конденсатор так же, как и индуктивность является реактивным сопротивлением.

20. Электрическая цепь переменного тока с индуктивностью и активным сопро­тивлением.

Реальные цепи, содержащие индуктивность, всегда имеют и активное сопротивление: сопротивление провода обмотки и подводящих проводов. Рассмотрим электрическую цепь, в которой через катушку индуктивности L, обладающую активным сопротивлением R, протекает переменный ток I = I_m∙sinωt.

Рис.4.17. Цепь с индуктивностью и активным сопротивлением.

Через катушку и резистор протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем строить вектор напряжения, приложенного к этой цепи. Напряжение, приложенное к цепи, равно векторной сумме падений напряжений на катушке индуктивности и на резисторе.

U = U_L + U_R

Напряжение на резисторе будет совпадать по фазе с током:

U_R = U_mR∙sinωt,

а напряжение на индуктивности будет равно ЭДС самоиндукции со знаком минус (по второму закону Кирхгофа).

U_L = L∙ 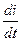= I_m∙ω∙L∙cosωt = U_mL∙sin(ωt + π/2)

Мы видим, что напряжение на индуктивности опережает ток на угол π/2. Построив векторы I, U_R и U_L и найдём вектор U. Векторная диаграмма показана на следующем рисунке.

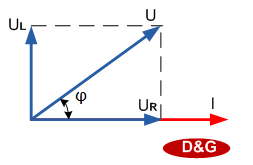
Рис.4.18. Векторная диаграмма цепи с индуктивностью и активным сопротивлением.

В рассматриваемой цепи ток I отстаёт по фазе от приложенного напряжения U, но не на π / 2, как в случае с чистой индуктивностью, а на некоторый угол φ. Этот угол может принимать любые значения от 0 до π/2 и при заданной индуктивности зависит от активного сопротивления. С увеличением R угол φ уменьшается. Как видно из диаграммы, модуль вектора U равен:

U = = I∙ = I∙Z₁, где

Z1 = называется полным сопротивлением цепи. Сдвиг по фазе между током и напряжением в данной цепи также определяется из векторной диаграммы:

tg φ = U_R / U_L = ωL / R

21.Электрическая цепь переменного тока с ёмкостью и активным сопротивлени­ем.

В реальных цепях переменного тока с ёмкостью всегда имеется активное сопротивление. Рассмотрим такую цепь.

Рис.4.22. Цепь с ёмкостью и активным сопротивлением.

Через конденсатор и резистор протекает один и тот же ток i = I_m∙sinωt. Поэтому в качестве основного выберем вектор тока и будем строить вектор напряжения, приложенного к этой цепи.

U = U_c + U_R.

Напряжение на резисторе будет совпадать по фазе с током:

U_R = U_mR∙sinωt.

Напряжение на конденсаторе будет отставать по фазе от тока на угол π / 2:

U_c = U_mc∙sin(ωt - π/2)

Построим векторы I, U_R и U_c и найдём вектор U. Построим векторную диаграмму.

Рис.4.23. Векторная диаграмма цепи с ёмкостью и активным сопротивлением.

Из векторной диаграммы следует, что ток I опережает по фазе приложенное напряжение U, но не на угол π/2, как в случае чистой ёмкости, а на угол φ. Этот угол может изменяться от 0 до π/2 и при заданной ёмкости С зависит от значения активного сопротивления: с увеличением R угол φ уменьшается.

Модуль вектора U равен:

U = = I 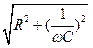= I∙Z₁, где

Z₁ = 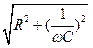(4.24) называется полным сопротивлением цепи.

Сдвиг по фазе между током и напряжением:

tgφ = Uc/U_R = (1/ωC)/R = 1/(ω∙R∙C).

22. Последовательное соединение катушки, конденсатора и резистора. Резонанс напряжений. Положительные и отрицательные моменты резонанса.

Последовательное соединение сопротивления, конденсатора и катушки

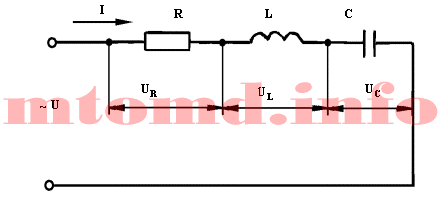
Рис. 1

Для анализа схемы разложим напряжение сети U на три составляющие:

· U_R — падение напряжения на активном сопротивлении;

· U_L — падение напряжения на индуктивном сопротивлении;

· U_C — падение напряжения на емкостном сопротивлении.

Ток в цепи I будет общим для всех элементов:

Проверку производят по формуле:

Следует отметить, что напряжения на отдельных участках цепи не всегда совпадают по фазе с током I.
Так, на активном сопротивлении падение напряжения совпадает по фазе с током, на индуктивном оно опережает по фазе ток на 90° и на емкостном — отстает от него на 90°. Графически это можно показать на векторной диаграмме.

Векторная диаграмма

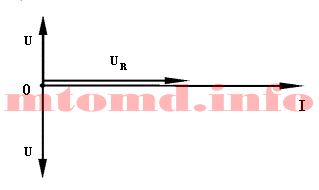
Рис. 2

Изображенные выше три вектора падения напряжений можно геометрически сложить в один.

Сложение трех векторов напряжения

Рис. 3

В таком соединении элементов возможны активно-индуктивный или активно-емкостный характеры нагрузки цепи. Следовательно, фазовый сдвиг имеет как положительный, так и отрицательный знак.

Резонанс напряжений. Условие резонанса напряжений.

Интересным является режим, когда нет сдвига по фазе. В этом случае:

Такой режим работы схемы называется резонансом напряжений. Полное сопротивление при резонансе напряжений имеет минимальное значение: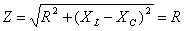

И при заданном напряжении U ток I может достигнуть максимального значения.

Из условия ωL = 1/ωC определим резонансную частоту:

Явления резонанса напряжений широко используется в радиотехнике и в отдельных промышленных установках.

23. Параллельное соединение катушки, конденсатора и резистора. Резонанс токов. Положительные и отрицательные моменты резонанса.

Электрические цепи однофазного тока. Параллельное соединение конденсатора и катушки. Резонанс токов.

Рассмотрим цепь параллельного включения конденсатора и катушки, обладающей активным сопротивлением и индуктивностью.

Параллельное соединение конденсатора и катушки

Рис. 1

В этой схеме общим параметром для двух ветвей является напряжение U. Первая ветвь — индуктивная катушка — обладает активным сопротивлением R и индуктивностью L. Результирующее сопротивление Z₁ и ток I₁ определяются по формуле:

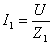
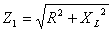Поскольку сопротивление этой ветви комплексное, то ток в ветви отстает по фазе от напряжения на угол φ₁ = arctg(R/X_L). Покажем это на векторной диаграмме.

Векторная диаграмма для первой ветви

Рис. 2

Спроецируем вектор тока I₁ на оси координат. Горизонтальная составляющая тока будет представлять собой активную составляющую I_1R, а вертикальная — I_1L. Количественные значения этих составляющих будут равны:

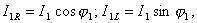
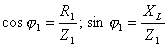
Во вторую ветвь включен конденсатор. Его сопротивление

Этот ток опережает по фазе напряжение на 90°. Для определения тока I в неразветвленной части цепи воспользуемся формулой:

Его значение можно получить и графическим путем, сложив векторы I₁ и I₂ (рис. 3). Угол сдвига между током и напряжением обозначим буквой φ. Здесь возможны различные режимы в работе цепи. При φ = +90° преобладающим будет емкостный ток, при φ = -90° — индуктивный.

Векторная диаграмма разветвленной цепи

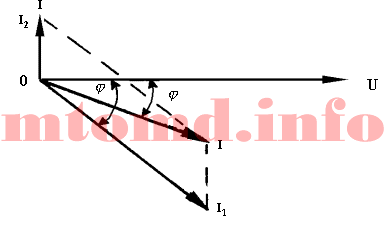
Рис. 3

Резонанс переменного тока. Условие резонанса токов.

Возможен режим, когда φ = 0, т.е. ток в неразветвленной части цепи I будет иметь активный характер. Произойдет это в случае, когда I_1L = I₂, т.е. при равенстве реактивных составляющих тока в ветвях. Такой режим называется резонансом токов. Также как в случае с резонансом напряжений, он широко применяется в радиотехнике.

Векторная диаграмма в режиме резонанса токов

Рис. 4

Рассмотренный выше случай параллельного соединения R, L и C может быть также проанализирован с точки зрения повышения cosφ для электроустановок. Известно, что cosφ является технико-экономическим параметром в работе электроустановок. Определяется он по формуле:

cosφ = P / S, где

Р — активная мощность электроустановок, кВт;
S — полная мощность электроустановок, кВт.

На практике cosφ определяют снятием со счетчиков показаний активной и реактивной энергии и, разделив одно показание на другое, получают tgφ. Далее по таблицам находят и cosφ.

Чем больше cosφ, тем экономичнее работает энергосистема, так как при одних и тех же значениях тока и напряжения (на которые рассчитан генератор) от него можно получить большую активную мощность.
Снижение cosφ приводит к неполному использованию оборудования и при этом уменьшается КПД установки. Тарифы на электроэнергию предусматривают меньшую стоимость 1 киловатт-часа при высоком cosφ, в сравнении с низким.

Мероприятия по повышению cosφ:

· недопущение холостых ходов электрооборудования;

· полная загрузка электродвигателей, трансформаторов и т.д.

Кроме этого, на cosφ положительно сказывается подключение к сети статических конденсаторов.

24. Активная, реактивная и полная мощность. Коэффициент мощности, его роль и способы повышения.

Мощность — работа в единицу времени по перемещению зарядов из А в B за некий период времени. С помощью закона Ома мощность на сопротивлении R можно выразить через ток и напряжение:

P=I*U=I²*R=U²/R

Эти формулы справедливы только при постоянном напряжении.

 Значение полной мощности S для переменного тока сформировано из корня квадратного суммы квадратов активной и реактивной составляющих. Полную мощность можно рассчитать с помощью активной и реактивной:

S=U*I= P²+Q²

(В*А), она равна произведению значений периодического I в цепи и U на контактах.

 Активная мощность — средняя за определенный период времени, в цепях однофазного синусоидального напряжения

P=U*I*cos φ

(Вт)

 Реактивная мощность характеризует нагрузку, созданную колебаниями энергии ЭМПоля в цепи синусоидального переменного напряжения.

Q=U*I*sin φ

(var — вар).

 Физически — это энергия для перемагничивания короткозамкнутой обмотки асинхронного двигателя во время его работы. Если нагрузка активно-индуктивная, то реактивная мощность будет положительной, если нагрузка активно-ёмкостного характера — отрицательной. Для измерения электрической мощности используют косвенный метод (вольтметр + амперметр), но обычно применяются ваттметры и варметры.

 Для полной мощности цепи:

S²=P²+N²

где N — неактивная мощность.

Дата добавления: 2015-05-06