Основы алгебры логики

Введем некоторые понятия, которые используются при построении логических устройств.

Логическим сообщением наз. такое сообщение истинность или ложность, которого может быть оценена однозначно. Каждое логическое сообщение может быть заменено математическим эквивалентом – логической функцией. Для описания взаимодействий между логическими сообщениями или логическими функциями введем понятие логическая операция.

Взаимосвязь логических переменных образует логическую функцию у = f(х). Так как аргумент и функция принимают конечное число значений, а именно только два значения (1 и 0), то число возможных логических функций всегда конечно и равно: N=2^m=2²ⁿ, где n- число независимых переменных, m=2ⁿ – число наборов независимых переменных. Для двух переменных имеем у=f(х₁, х₂), N=2²ⁿ=16. (таблица 6.1.)

Таким образом, для двух переменных имеем 16 логических функций.

Все операции над логическими функциями совершаются при помощи законов алгебры логики.

Отличие алгебры логики от обычной алгебры заключается в том, что функции могут принимать значения только 0, 1. Обработка информации, которая дается в виде действия, ведется в двоичной системе, которая имеет только две цифры 0,1.

Задача алгебры логики заключается в том чтобы:

1. Математически записывать логические сообщения и связи между ними.

2. Реализовывать логические уравнения в виде логических схем, т.е. переход от аналитических описаний к логическим автоматам.

3. Производить реализацию логических автоматов в оптимальном виде.

Таблица 3.1.

Основные законы алгебры логики.

1.Закон действия с единицей.

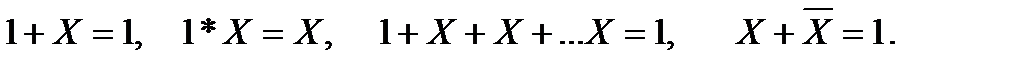
2 Закон действия с нулем.

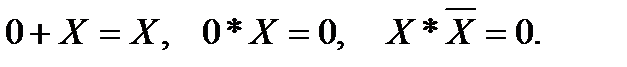
3.Закон повторяемости

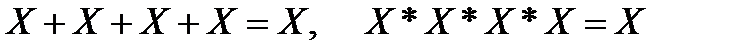
4 Закон отрицания отрицания.

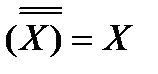
5 Переместительный закон

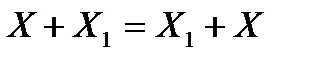
6. Сочетательный закон

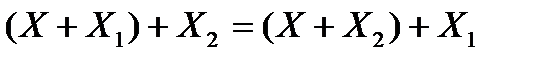
7. Распределительный закон

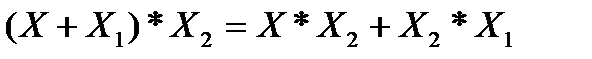
8. Закон поглощения

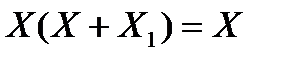
9. Закон склейки

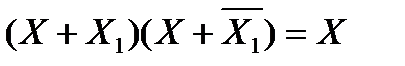
10. Закон де Моргана

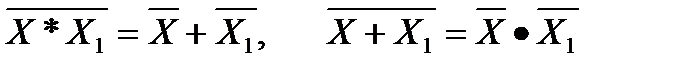
Если записывать логические функции в виде суммы произведений переменных, то такая запись ДНФ. Если записывать в виде произведения сумм переменных, то такая запись КНФ. Логические функции наиболее полно представляются

в таблице 6.1.истинности, где каждая комбинация независимых переменных указывает на значение логической функции. Исходя, из таблицы истинности можно сказать, что при сочетании переменных, когда функция принимать значение 1, это конституентой единицы или минтермой. Если функция принимает значение 0, то это конституента нуля или макстерма.

Дата добавления: 2015-05-06