Вопрос. Представление синусоидальных величин в виде вращающихся векторов на декартовой плоскости, в комплексной форме

Метод двух узлов

Для цепей, содержащих два узла или сводящихся к таковым, можно применять метод двух узлов. При полностью графическом способе реализации метода он заключается в следующем:

Строятся графики зависимостей токов во всех i-х ветвях в функции общей величины — напряжения между узлами m и n, для чего каждая из исходных кривых смещается вдоль оси напряжений параллельно самой себе, чтобы ее начало находилось в точке, соответствующей ЭДС в i-й ветви, а затем зеркально отражается относительно перпендикуляра, восстановленного в этой точке.

Определяется, в какой точке графически реализуется первый закон Кирхгофа. Соответствующие данной точке токи являются решением задачи.

Метод двух узлов может быть реализован и в другом варианте, отличающемся от изложенного выше меньшим числом графических построений.

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями и представить в виде вращающихся векторов на декартовой или комплексной плоскости.

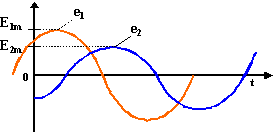
Рисунок 2.3 - Графическое изображение синусоидальных напряжений

Запишем синусоидальные напряжения с помощью тригонометрических функций: 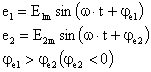. (2.15)

Значения в скобках синуса называют фазами синусоид, а значения фазы в начальный момент времени - начальной фазой.

Величина ω называется угловой частотой: 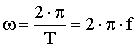, [рад/с] (2.16)

Где Т - период [c]; f - частота [Гц].

При совместном рассмотрении двух синусоидально изменяющихся величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз: 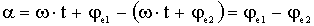. (2.17)

Если α=0, то говорят, что сигналы синфазны, если α=π, то говорят, что сигналы в противофазе. Если α=+π/2 - в квадратуре. Т.е. е₂ отстаёт от е₁ на угол α.

При изображении синусоидальных ЭДС, напряжений и токов вращающимися векторами на декартовой плоскости из начала координат проводят векторы, равные амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки с угловой скоростью ω. Фазовый угол отсчитывают от положительной оси абсцисс.

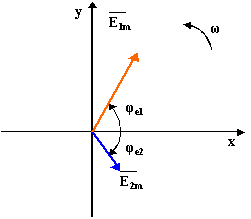
Рисунок 2.4 - Изображение синусоидальных напряжений вращающимися векторами

Проекции вращающихся векторов на ось ординат равны мгновенным значениям.

Совокупность векторов, изображающих синусоидальные ЭДС, напряжения и токи одной частоты, называют векторными диаграммами. При построении векторных диаграмм часто удобно принимать t=0. При этом сложение и вычитание синусоидально изменяющихся величин можно заменить сложением и вычитанием их векторов: 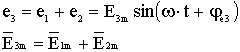. (2.18)

Результирующие напряжение также будет синусоидальным.

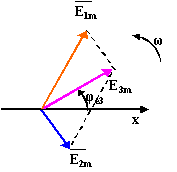Рисунок 2.5 - Изображение суммы двух синусоидальных напряжений в виде вращающегося вектора

Определение амплитуды E_3m и начальной фазы φ_e3 можно осуществить сложением изображающих их векторов. Вычитание мгновенных значений можно заменить вычитанием изображающих векторов .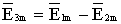

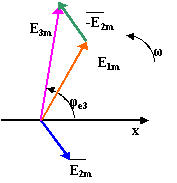Рисунок 2.6 - Изображение разности двух синусоидальных напряжений в виде вращающегося вектора

Дата добавления: 2015-05-06