Дешифраторы и шифраторы

Дешифраторы. Каждому цифровому сигналу на входах дешифратора соответствует логическая 1 (или логический 0) на определенном выходе. Так, на одном выходе дешифратора появляется логическая 1, а на остальных-логические 0, когда на входных шинах устанавливается, к примеру, двоичный код десятичного числа «четыре»; логическая 1 на другом выходе и логические 0 на остальных появляются, когда на шинах присутствует двоичный код десятичного числа «пять» и т.д. Таким образом, дешифратор расшифровывает (дешифрирует) число, записанное в двоичном коде, представляя его логической 1 (логическим 0) на определенном выходе. Число входов дешифратора равно количеству разрядов поступающих двоичных чисел, а число его выходов — полному количеству различных двоичных чисел этой разрядности. Так как каждый разряд двоичного кода принимает два значения, то полное количество n-разрядных комбинаций (n-разрядных двоичных чисел) равно 2n. Такое число выходов имеет любой полный дешифратор. Рассмотрим принцип, заложенный в основе построения дешифратора.

Чтобы выяснить, является ли данное двоичное число ожидаемым, нужно инвертировать цифры в определенных разрядах данного числа (где в ожидаемом числе записаны нули), а затем перемножить цифры всех разрядов преобразованного таким образом числа. Если результатом перемножения будет единица, то данное число является ожидаемым. Если в результате указанных действий появится нуль, это означает, что нули находятся не в тех или не только в тех разрядах, где они стоят в ожидаемом числе. Поэтому после инверсии цифр в определенных разрядах не все цифры преобразованного числа оказались единицами и их перемножение дало нуль. В соответствии с изложенным дешифратор можно построить на инверторах и конъюнкторах, выходы которых являются выходами дешифратора. Чтобы на выходе данного конъюнктора появлялась логическая 1, когда на входных шинах присутствует определенный двоичный код, надо соответствующим образом соединить шины с входами конъюнктора. Легко понять, что одни входы конъюнктора должны соединяться непосредственно с теми шинами, на которых при данном коде присутствуют единицы; другие входы с оставшимися шинами должны быть соединены через инверторы. Пусть на выходе определенного конъюнктора надо получить логическую единицу, если на входных шинах появится, к примеру, код 01011, представляемый совокупностью высоких и низких потенциалов. Если инвертировать потенциалы на шинах третьего и пятого разрядов и реализовать конъюнкцию инвертированных и неинвертированных потенциалов, то результатом будет 1. Очевидно, что если на входных шинах присутствует совокупность потенциалов, отличающаяся от предыдущей хотя бы в одном разряде, то результатом описанных действий будет 0. Изложенный принцип положен в основу построения схемы на рис. 3.20. Логическая 1 на выходе y0 должна фиксировать присутствие на входных шинах х3, х2, x1 двоичного кода 000 десятичного числа 0; поэтому входы верхнего по схеме конъюнктора должны быть соединены с шинами х3, х2, x1, на каждой из которых присутствует логическая 1, когда на входных шинах х3 = x2 = x1 = 0. Логическая 1, к примеру, на выходе y2 фиксирует появление на входных шинах х3, х2, x1 кода десятичного числа 2 (010); поэтому входы соответствующего конъюнктора должны быть соединены с шинами х3, х2, x1, на каждой из которых имеется логическая 1, когда х3 = 0, х2 = 1, x1 = 0. Аналогично соединяются с шинами входы других конъюнкторов. Дешифратор (рис. 3.20) называется линейным (матричным, одноступенчатым). В нем каждый конъюнктор получает информацию о всех n разрядах кода, поэтому число его входов равно n (в данном случае — трем).__

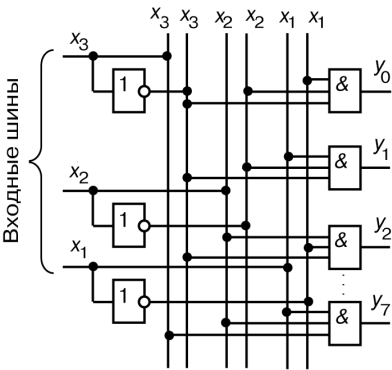
Рис. 3.20. Линейный дешифратор

Дешифраторы широко используются в цифровой аппаратуре. Так, к одному из его выходов может быть подключено управляемое устройство, на которое будет поступать логический сигнал, когда на входах дешифратора установится определенный двоичный код.

Шифраторы. Шифратор решает задачу, обратную дешифратору: на его выходных шинах устанавливается код, соответствующий номеру входа, на котором появилась логическая 1.

При построении шифратора для получения натурального двоичного кода учитывают, что единицу в младшем разряде такого кода имеют нечетные десятичные цифры 1, 3, 5, 7, т.е. на выходной шине младшего разряда должна быть 1, если она есть на входной шине № 1 или на входной шине № 3 и т.д. Поэтому входные шины под указанными номерами через элемент ИЛИ соединяются с выходной шиной младшего разряда. Единицу во втором разряде двоичного кода имеют десятичные цифры 2, 3, 6, 7,...; шины с этими номерами через элемент ИЛИ должны подключаться к выходу шифратора, на котором устанавливается второй разряд кода. Аналогично шины с номерами 4, 5, 6, 7,... через элемент ИЛИ должны быть соединены с выходом, на котором устанавливается третий разряд, так как их коды имеют в этом разряде единицу, и т.д. Схема шифратора, построенная в соответствии с изложенным принципом, изображена на рис. 3.23. Условное изображение шифратора приведено на рис. 3.24.

Шифраторы применяются в устройствах, преобразующих один вид кода в другой. При этом вначале дешифрируется каждая комбинация исходного кода, в результате чего на соответствующем выходе дешифратора появляется логическая 1. Затем этот логический сигнал, значение которого определено номером выхода дешифратора, подается на шифратор, и на его выходах устанавливается преобразованный код.

Примером использования шифраторов являются также устройства ввода двоичных кодов в цифровое устройство с клавиатуры. При нажатии клавиши на определенной входной шине шифратора появляется логическая 1 (шина возбуждается) и на выходах устанавливается двоичный код, соответствующий нанесенному на клавишу знаку (букве, цифре и т.д.).

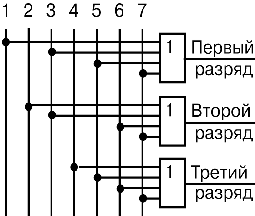
Рис. 3.23. Схема шифратора Рис. 3.24. Условное изображение шифратора

Дата добавления: 2015-05-06