Коэффициент пульсаций. Коэффициент пульсации выпрямленного напряжения

Коэффициент пульсации выпрямленного напряжения

Трехфазные выпрямители с нейтральным проводом

Трехфазный однополупериодный выпрямитель или трехфазный выпрямитель с нейтральным проводом (Рисунок 4) можно представить как три однофазных однополупериодных выпрямителя, включенных параллельно на одну нагрузку.

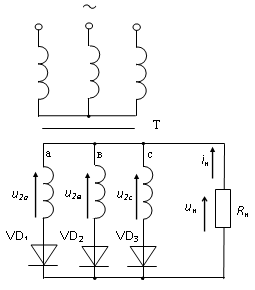
Рисунок 4. Схема трехфазного выпрямителя с нейтральным проводом

Рисунок 5. Временные диаграммы напряжений и токов трехфазного выпрямителя с нейтральным проводом

Однако из-за сдвига фаз выпрямляемых переменных напряжений напряжение на нагрузке не падает до нуля. Каждый диод в открытом состоянии находится треть периода, когда прямое напряжение на нем больше, чем на других.

Среднее напряжение на нагрузке у данного выпрямителя определяется выражением а коэффициент пульсации k_n= 0,25. Обратное максимальное напряжение на каждом из диодов равно амплитуде линейного напряжение, т.е.

Выпрямленное напряжение (ЭДС) - 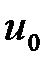, 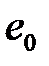(напряжение до ФУ) как любую периодическую несинусоидальную функцию можно разложить в ряд Фурье, т.е. представить в виде суммы постоянной составляющей и суммы переменных гармонических составляющих. Первый член разложения в ряд Фурье – постоянная составляющая 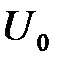(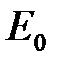) – среднее значение выпрямленного напряжения (ЭДС). Сумма переменных гармонических составляющих называется напряжением пульсаций 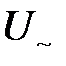(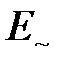). Также можно представить в виде суммы постоянной 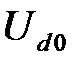и пульсирующей 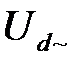составляющих напряжение в нагрузке (напряжение после ФУ). Значение пульсации задается коэффициентом пульсаций, равным отношению максимального значения пульсации к постоянной составляющей напряжения:

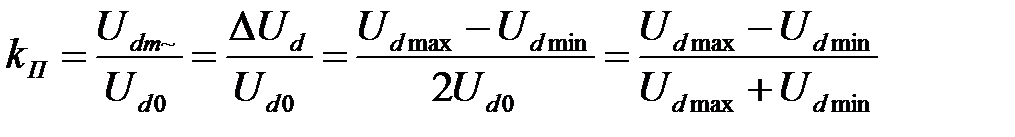, (1.6)

где 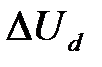- полуразность между наибольшим и наименьшим мгновенными значениями напряжения в нагрузке (рис. 1.12). Аналогично можно записать выражения для коэффициента пульсаций выпрямленного напряжения .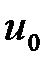

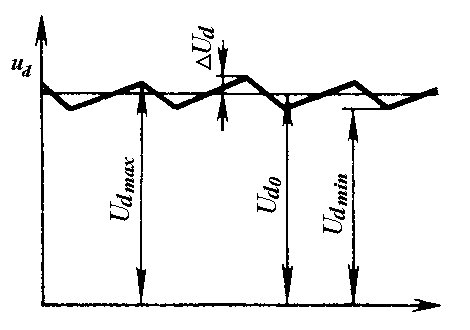
Рис. 1.12. График напряжения с постоянной составляющей 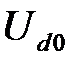и пульсирующей .

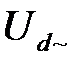Также пользуются коэффициентом пульсаций k -й гармоники, который равен отношению амплитуды k -й гармонической напряжения пульсаций к среднему значению напряжения

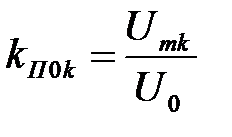(до ФУ) и 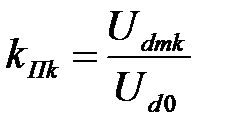(после ФУ) (1.7)

Следует отметить, что во многих литературных источниках по электронике под коэффициентом пульсаций называют коэффициент пульсаций 1-й гармоники, равный отношению амплитуды первой (основной) гармоники напряжения пульсаций к среднему значению напряжения. Это верно, если суммой высших гармонических напряжения пульсаций относительно первой (основной) можно пренебречь.

Известно, что для выпрямителя без ФУ коэффициент пульсаций по k -й гармонике выпрямленной ЭДС:

,

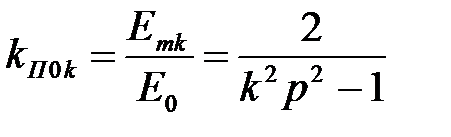где p – число пульсаций в кривой выпрямленного напряжения (пульсность схемы выпрямления). При p = 2 получим 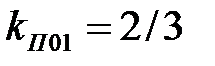, 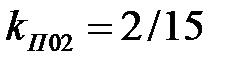и амплитуда 2-й гармонической составляет 20% от первой (основной) гармоники. При p = 6 получим 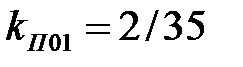, 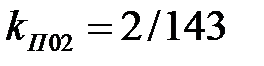и амплитуда 2-й гармонической составляет 24,5% от первой (основной) гармоники.

Резистивно-емкостной усилитель. Принцип действия и схема.

Дата добавления: 2015-05-06