
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод последовательных интервалов. Шпоры по электротехнике от группы А4-08 и Ко
|
|
|
|
Шпоры по электротехнике от группы А4-08 и Ко.
Материал набирали: Арсен Авалян, Анастасия Байкова, Камила Мишакина, Светлана Щербатых, Николай Гудков, Константин Кутузов, Зохраб Ахундов.
Тщательную проверку и исправление большинства ошибок осуществил Зохраб Ахундов (А4-05).
Обработал Михаил Моргунов.
U(p,x)= 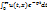 ;
;
I(p,x)= 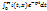 ;
;
γ = 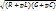 =p
=p  =p/V
=p/V
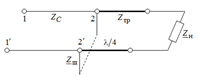 Рис.13.17. Согласование линии с помощью четвертьволнового трансформатора и параллельного шлейфа
Путем подбора волнового сопротивления четвертьволнового трансформатора добиваются согласования активной проводимости цепи трансформатор-нагрузка, а затем с помощью шлейфа компенсируют реактивную составляющую проводимости ветви с трансформатором. Подключают короткозамкнутый или разомкнутый шлейф, реактивное сопротивление которого равно по величине и противоположно по знаку реактивной составляющей входного сопротивления линии. При этом в линии устанавливается чисто бегущая волна, и вся энергия от генератора передается без отражения к нагрузке.
Z H = R H + j X H;
Рис.13.17. Согласование линии с помощью четвертьволнового трансформатора и параллельного шлейфа
Путем подбора волнового сопротивления четвертьволнового трансформатора добиваются согласования активной проводимости цепи трансформатор-нагрузка, а затем с помощью шлейфа компенсируют реактивную составляющую проводимости ветви с трансформатором. Подключают короткозамкнутый или разомкнутый шлейф, реактивное сопротивление которого равно по величине и противоположно по знаку реактивной составляющей входного сопротивления линии. При этом в линии устанавливается чисто бегущая волна, и вся энергия от генератора передается без отражения к нагрузке.
Z H = R H + j X H;
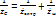 =
= 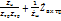 =
=  =
= 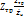 ;
; 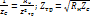
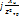 =
= 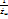 ;
; 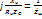 ;
В зависимости от характера нагрузки применяют шлейф, работающий в режиме короткого замыкания (X H > 0) или холостого хода (X H < 0).
;
В зависимости от характера нагрузки применяют шлейф, работающий в режиме короткого замыкания (X H > 0) или холостого хода (X H < 0).
 2) Переход волны из одной линии в другую. На практике приходится соединять между собой разные линии. В месте соединения (стыка) линий часто включают сосредоточенные элементы (R, L, C), назначение которых: ограничение перенапряжений, ограничение токов КЗ, увеличение пропускной способности линии, уменьшение искажений и т.д. Пусть известная прямоугольная падающая волна (uпад = U 0; iпад = U 0/ Z C) переходит из одной линии с Z C1 и v 1 в другую с Z C2 и v 2 через индуктивность L (рис.9.13). Когда она достигнет места стыка двух линий, часть её отразится и в первой линии возникнет отраженная волна, которая со скоростью v 1 будет перемещаться к её началу. Но часть волны проникнет во вторую линию. Эту волну называют преломленной, она со скоростью v 2 будет перемещаться от начала к концу второй линии. Для расчета отраженных и преломленных волн обратимся к схеме замещения с сосредоточенными параметрами, представив последовательно соединенные L и Z C2 нагрузкой первой линии (рис.9.14). В этой схеме необходимо любым методом рассчитать ПП (чаще всего применяется классический или операторный метод).
Если переходный процесс в схеме замещения рассчитывать операторным методом, то для определения отраженных волн целесообразно использовать коэффициент отражения, а именно – определять изображения:
2) Переход волны из одной линии в другую. На практике приходится соединять между собой разные линии. В месте соединения (стыка) линий часто включают сосредоточенные элементы (R, L, C), назначение которых: ограничение перенапряжений, ограничение токов КЗ, увеличение пропускной способности линии, уменьшение искажений и т.д. Пусть известная прямоугольная падающая волна (uпад = U 0; iпад = U 0/ Z C) переходит из одной линии с Z C1 и v 1 в другую с Z C2 и v 2 через индуктивность L (рис.9.13). Когда она достигнет места стыка двух линий, часть её отразится и в первой линии возникнет отраженная волна, которая со скоростью v 1 будет перемещаться к её началу. Но часть волны проникнет во вторую линию. Эту волну называют преломленной, она со скоростью v 2 будет перемещаться от начала к концу второй линии. Для расчета отраженных и преломленных волн обратимся к схеме замещения с сосредоточенными параметрами, представив последовательно соединенные L и Z C2 нагрузкой первой линии (рис.9.14). В этой схеме необходимо любым методом рассчитать ПП (чаще всего применяется классический или операторный метод).
Если переходный процесс в схеме замещения рассчитывать операторным методом, то для определения отраженных волн целесообразно использовать коэффициент отражения, а именно – определять изображения:  ;
; 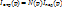 ; где N(p)=
; где N(p)= 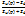 . Для нашего конкретного примера: N(p)=
. Для нашего конкретного примера: N(p)= 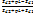 .
.
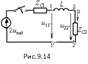 Определение преломленных волн также производится по схеме замещения. Для этого нужно рассчитать напряжение u 22’ в конце или ток в начале второй линии. В нашем случае:
Определение преломленных волн также производится по схеме замещения. Для этого нужно рассчитать напряжение u 22’ в конце или ток в начале второй линии. В нашем случае: 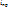 =i=
=i= 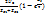 ,
, 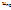 =
= 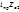 =
= 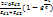 , где
, где  . Эти формулы определяют преломленные волны как функции времени в начале второй линии. Чтобы получить полное выражение преломленных волн, необходимо в полученных выражениях t заменить на t-х/v 2, где х – расстояние от начала второй линии до любой её точки.
. Эти формулы определяют преломленные волны как функции времени в начале второй линии. Чтобы получить полное выражение преломленных волн, необходимо в полученных выражениях t заменить на t-х/v 2, где х – расстояние от начала второй линии до любой её точки.
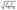 , и уравнения, связывающие токи и напряжения обмоток, имеют вид:
(11.8) Величина
, и уравнения, связывающие токи и напряжения обмоток, имеют вид:
(11.8) Величина 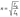 называется коэффициентом трансформации.
Из (10.7), (10.8) и (10.13) следует, что коэффициент трансформации равен отношению числа витков вторичной обмотки N2 к числу первичной N1:
n = N2/N1. (11.9)
C учётом (11.9) и (11.6) выражения (11.8) будут иметь вид:
называется коэффициентом трансформации.
Из (10.7), (10.8) и (10.13) следует, что коэффициент трансформации равен отношению числа витков вторичной обмотки N2 к числу первичной N1:
n = N2/N1. (11.9)
C учётом (11.9) и (11.6) выражения (11.8) будут иметь вид:
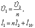 (11.10) Согласно выражениям (11.10) отношение напряжения на вторичной обмотке совершенного трансформатора к напряжению первичной равно коэффициенту трансформации и не зависит от сопротивления нагрузки.
Идеальный трансформатор
Совершенный трансформатор, ток намагничивания которого равен нулю, называется идеальным трансформатором. Компонентные уравнения идеального трансформатора, согласно (11.10), имеют вид:
(11.11) Из компонентных уравнений следует, что при любом значении сопротивления нагрузки отношение напряжения вторичной обмотки к напряжению первичной идеал. трансформ. равно отнош. токов и обмоток:
(11.10) Согласно выражениям (11.10) отношение напряжения на вторичной обмотке совершенного трансформатора к напряжению первичной равно коэффициенту трансформации и не зависит от сопротивления нагрузки.
Идеальный трансформатор
Совершенный трансформатор, ток намагничивания которого равен нулю, называется идеальным трансформатором. Компонентные уравнения идеального трансформатора, согласно (11.10), имеют вид:
(11.11) Из компонентных уравнений следует, что при любом значении сопротивления нагрузки отношение напряжения вторичной обмотки к напряжению первичной идеал. трансформ. равно отнош. токов и обмоток:
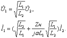
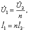
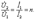 (11.12) В связи с тем, что коэффициент трансформации n является действительным числом, напряжение и ток первичной обмотки имеют такие же начальные фазы, как соответственно вторичной обмотки, отличаются от них только по амплитуде.
Из выражений (11.12) следует, что мгновенная и комплексная мощности, потребляемые первичной обмоткой, равны мгновенной комплексной мощностям, отдаваемым идеальным трансформатором в нагрузку:
(11.12) В связи с тем, что коэффициент трансформации n является действительным числом, напряжение и ток первичной обмотки имеют такие же начальные фазы, как соответственно вторичной обмотки, отличаются от них только по амплитуде.
Из выражений (11.12) следует, что мгновенная и комплексная мощности, потребляемые первичной обмоткой, равны мгновенной комплексной мощностям, отдаваемым идеальным трансформатором в нагрузку:
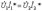 . КПД идеального трансформатора равен единице.
Если к зажимам 2 — 2’ идеального трансформ. подкл. сопрот. нагр. Zн, то его входное сопр. со стороны зажимов 1 – 1’ равно
. КПД идеального трансформатора равен единице.
Если к зажимам 2 — 2’ идеального трансформ. подкл. сопрот. нагр. Zн, то его входное сопр. со стороны зажимов 1 – 1’ равно
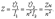 (11.13) Таким образом, входное сопротивление идеального трансформатора отличается от сопротивления нагрузки в n2 раз. Это свойство широко используется в радиоэлектронных устройствах для согласования сопротивления источника энергии с нагрузкой.
В отличие от идеального, в реальном трансформаторе происходят потери энергии, он характеризуется ряде случаев значительными паразитными емкостями, индуктивность его обмоток имеет конечное значение, а потоки рассеяния не равны нулю. Как правило, при разработке конструкции трансформатора принимается ряд мер, направленных на приближение свойств к свойствам идеального трансформатора.
(11.13) Таким образом, входное сопротивление идеального трансформатора отличается от сопротивления нагрузки в n2 раз. Это свойство широко используется в радиоэлектронных устройствах для согласования сопротивления источника энергии с нагрузкой.
В отличие от идеального, в реальном трансформаторе происходят потери энергии, он характеризуется ряде случаев значительными паразитными емкостями, индуктивность его обмоток имеет конечное значение, а потоки рассеяния не равны нулю. Как правило, при разработке конструкции трансформатора принимается ряд мер, направленных на приближение свойств к свойствам идеального трансформатора.
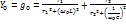
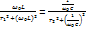 – Условие резонанса токов (равенство реактивных проводимостей).
Отсюда
– Условие резонанса токов (равенство реактивных проводимостей).
Отсюда 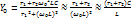 При
При 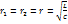 (условие безразличного резонанса),
(условие безразличного резонанса), 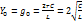
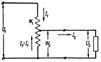 Преимуществом автотрансформ. является более высокий КПД, поскольку лишь часть мощности подвергается преобразованию — это особенно существенно, когда входное и выходное напряжения отличаются незначительно. Недостатком является отсутствие электрической изоляции (гальванической развязки) между первичной и вторичной цепью. В промышленных сетях, где наличие заземления нулевого провода обязательно, этот фактор роли не играет, зато существенным является меньший расход стали для сердечника, меди для обмоток, меньший вес и габариты, и в итоге — меньшая стоимость.
Принцип работы автотрансформ.. Предположим, что источник электрической энергии (сеть переменного тока) подключен к виткам
Преимуществом автотрансформ. является более высокий КПД, поскольку лишь часть мощности подвергается преобразованию — это особенно существенно, когда входное и выходное напряжения отличаются незначительно. Недостатком является отсутствие электрической изоляции (гальванической развязки) между первичной и вторичной цепью. В промышленных сетях, где наличие заземления нулевого провода обязательно, этот фактор роли не играет, зато существенным является меньший расход стали для сердечника, меди для обмоток, меньший вес и габариты, и в итоге — меньшая стоимость.
Принцип работы автотрансформ.. Предположим, что источник электрической энергии (сеть переменного тока) подключен к виткам  обмотки автотрансформ., а нагрузка — к некоторой части этой обмотки
обмотки автотрансформ., а нагрузка — к некоторой части этой обмотки  . При прохождении перемен. тока по обмотке автотрансформ. возникает перем. магн. поток, индуктирующий в этой обмотке электродвижущую силу, величина которой прямо пропорциональна числу витков обмотки. Следовательно, если во всей обмотке автотрансформ., имеющей число витков
. При прохождении перемен. тока по обмотке автотрансформ. возникает перем. магн. поток, индуктирующий в этой обмотке электродвижущую силу, величина которой прямо пропорциональна числу витков обмотки. Следовательно, если во всей обмотке автотрансформ., имеющей число витков  , индуктируется электродвижущая сила
, индуктируется электродвижущая сила  , то в части этой обмотки, имеющей число витков
, то в части этой обмотки, имеющей число витков  , индуктируется электродвижущая сила
, индуктируется электродвижущая сила  . Соотношение величин этих ЭДС выглядит так:.
. Соотношение величин этих ЭДС выглядит так:. 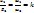 где
где  — коэффициент трансформации. Т.к. падение напряжения в активном сопротивлении обмотки автотрансформ. относительно мало, то им практически можно пренебречь и считать справедливыми равенства
— коэффициент трансформации. Т.к. падение напряжения в активном сопротивлении обмотки автотрансформ. относительно мало, то им практически можно пренебречь и считать справедливыми равенства 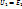 и
и 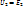 где
где  — напряжение источника электрической энергии, поданное на всю обмотку автотрансформ., имеющую число витков
— напряжение источника электрической энергии, поданное на всю обмотку автотрансформ., имеющую число витков  ;
;  — напряжение на нагрузке, снимаемое с той части обмотки автотрансформ., которая обладает количеством витков
— напряжение на нагрузке, снимаемое с той части обмотки автотрансформ., которая обладает количеством витков  . Следовательно,
. Следовательно, 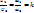 .
Если к автотрансформатору подкл. нагрузка, то под влиянием напряжения
.
Если к автотрансформатору подкл. нагрузка, то под влиянием напряжения  в нём возникает электр. ток, действ. знач. которого обозначим как
в нём возникает электр. ток, действ. знач. которого обозначим как  . Соответственно, в первичной цепи автотрансформ. будет ток, действующее значение которого обозначим как
. Соответственно, в первичной цепи автотрансформ. будет ток, действующее значение которого обозначим как  . Однако ток в верхней части обмотки автотрансформ., имеющей число витков
. Однако ток в верхней части обмотки автотрансформ., имеющей число витков 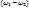 будет отличаться от тока в нижней её части, имеющей количество витков
будет отличаться от тока в нижней её части, имеющей количество витков  . Это объясняется тем, что в верхней части обмотки протекает только ток
. Это объясняется тем, что в верхней части обмотки протекает только ток  , а в нижней части — некоторый результирующий ток, представляющий собой разность токов
, а в нижней части — некоторый результирующий ток, представляющий собой разность токов  и
и  . Согласено правилу Ленца индуктированное электр. поле в обмотке автотрансформ.а
. Согласено правилу Ленца индуктированное электр. поле в обмотке автотрансформ.а  направл. навстречу электрич. полю, созданному в ней источником электр. энергии. Поэтому токи
направл. навстречу электрич. полю, созданному в ней источником электр. энергии. Поэтому токи  и
и  в нижней части обмотки автотрансформ. направл. навстречу друг другу, то есть находятся в противофазе. Сами токи
в нижней части обмотки автотрансформ. направл. навстречу друг другу, то есть находятся в противофазе. Сами токи  и
и  , как и в обычном трансформ., связаны соотнош.
, как и в обычном трансформ., связаны соотнош. 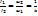 Так как в понижающем трансформаторе
Так как в понижающем трансформаторе 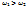 , то
, то 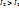 и результирующий ток в нижней обмотке автотрансформатора равен
и результирующий ток в нижней обмотке автотрансформатора равен 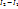 . Следовательно, в той части обмотки автотрансформатора, с которой подаётся напряжение на нагрузку, ток значительно меньше тока в нагрузке, то есть
. Следовательно, в той части обмотки автотрансформатора, с которой подаётся напряжение на нагрузку, ток значительно меньше тока в нагрузке, то есть 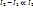 .
.
 На основании второго закона Кирхгофа:
На основании второго закона Кирхгофа: 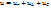 При синусоидальном напряжении эта формула переходит в:
При синусоидальном напряжении эта формула переходит в: 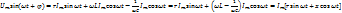 Где
Где  – реактивное сопротивление. Отсюда находим
– реактивное сопротивление. Отсюда находим 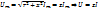 и
и 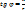 где
где 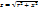 – полное сопротивление.
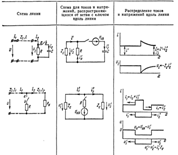
Электрическая цепь с параллельным соединением элементов.
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением. На основании первого закона Кирхгофа:
– полное сопротивление.
Электрическая цепь с параллельным соединением элементов.
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением. На основании первого закона Кирхгофа: 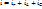 При синусоидальном токе эта формула переходит в:
При синусоидальном токе эта формула переходит в: 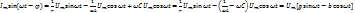 Где
Где 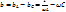 – реактивная проводимость.
– реактивная проводимость. 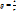 – активная проводимость. Отсюда находим
– активная проводимость. Отсюда находим 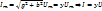 и
и 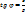 где
где  – полное сопротивление.
Электрическая цепь со смешанным соединением элементов.
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Векторные и топографические диаграммы. Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока, к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения, ориентируя относительно него векторы токов в параллельных ветвях. Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
– полное сопротивление.
Электрическая цепь со смешанным соединением элементов.
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
Векторные и топографические диаграммы. Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока, к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения, ориентируя относительно него векторы токов в параллельных ветвях. Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
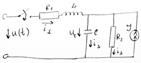 Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных. Количество переменных состояния (число уравнений) равно числу независимых накопителей энергии. Уравнения состояния должны удовлетворять требованиям независимости уравнений и возможностью восстановления на основе переменных состояния любых других переменных.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах (начальные значения этих переменных относятся к независимым). Зная закон изменения этих переменных во времени их можно заменить источниками ЭДС и тока с известными параметрами, а остальная цепь станет резистивной.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные
Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных. Количество переменных состояния (число уравнений) равно числу независимых накопителей энергии. Уравнения состояния должны удовлетворять требованиям независимости уравнений и возможностью восстановления на основе переменных состояния любых других переменных.
Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах (начальные значения этих переменных относятся к независимым). Зная закон изменения этих переменных во времени их можно заменить источниками ЭДС и тока с известными параметрами, а остальная цепь станет резистивной.
При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные 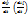 и
и 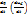 с самими переменными
с самими переменными 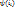
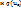 и источниками внешних воздействий (источниками ЭДС и тока), необходимо составить систему алгебр. урав., связывающих иском. величины с переменными состояния и источник. внешних воздействий.
В качестве примера рассмотрим цепь, в которой требуется определить токи
и источниками внешних воздействий (источниками ЭДС и тока), необходимо составить систему алгебр. урав., связывающих иском. величины с переменными состояния и источник. внешних воздействий.
В качестве примера рассмотрим цепь, в которой требуется определить токи 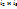
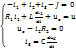
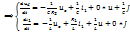
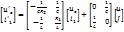
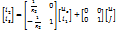 Вектор начальных значений
Вектор начальных значений 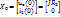
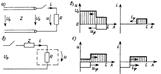 Возникшая на оконечных зажимах волна движется к началу линии, и в ходе ее распространения вдоль линии устанавливается напряжение U 0 R /(Z + R) (рис. 26.10, в). При t = t 1 = l / v в начале линии происходит ее отражение от разомкнутых входных зажимов с коэффициентами отражения Nu = 1 и Ni = – 1. Возникшая новая волна u j, таким образом, сохраняет отрицательный знак u j = u y = – U 0 Z /(Z + R) и приводит к уменьшению напряжения на линии (рис. 26.10, г) до значения U 0 + u y + u j = U 0(1 – 2 Z /(Z + R)) = U 0(R – Z)/(R + Z). Отсюда следует, что при R < Z в результате отражения от входных зажимов результирующее напряжение на линии изменяет знак. При R > Z отражение от входных зажимов ведет к уменьшению напряжения при сохранении его знака. При разряде на согласованную нагрузку (R = Z) и после отражения на входе напряжение на линии спадает до нуля. Ток в линии после отражения от разомкнутых входных зажимов уменьшается до нуля.
При R = Z — в согласованном режиме — к моменту прихода прямой волны u j на нагрузку переходный процесс заканчивается — в течение времени 0 < t < 2 l / v через нагрузку протекает прямоугольный импульс тока с амплитудой напряжения u = U 0/2, обеспечивая выделение в ней максимальной мощности:
Возникшая на оконечных зажимах волна движется к началу линии, и в ходе ее распространения вдоль линии устанавливается напряжение U 0 R /(Z + R) (рис. 26.10, в). При t = t 1 = l / v в начале линии происходит ее отражение от разомкнутых входных зажимов с коэффициентами отражения Nu = 1 и Ni = – 1. Возникшая новая волна u j, таким образом, сохраняет отрицательный знак u j = u y = – U 0 Z /(Z + R) и приводит к уменьшению напряжения на линии (рис. 26.10, г) до значения U 0 + u y + u j = U 0(1 – 2 Z /(Z + R)) = U 0(R – Z)/(R + Z). Отсюда следует, что при R < Z в результате отражения от входных зажимов результирующее напряжение на линии изменяет знак. При R > Z отражение от входных зажимов ведет к уменьшению напряжения при сохранении его знака. При разряде на согласованную нагрузку (R = Z) и после отражения на входе напряжение на линии спадает до нуля. Ток в линии после отражения от разомкнутых входных зажимов уменьшается до нуля.
При R = Z — в согласованном режиме — к моменту прихода прямой волны u j на нагрузку переходный процесс заканчивается — в течение времени 0 < t < 2 l / v через нагрузку протекает прямоугольный импульс тока с амплитудой напряжения u = U 0/2, обеспечивая выделение в ней максимальной мощности:
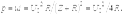 Описанный режим используют в импульсной технике для формирования прямоугольных импульсов тока. Если условие согласования не выполнено, то переходный процесс состоит из бесконечного числа отражений волн на нагрузке и на входе. В этом случае при R > Z напряжение на нагрузке изменяется монотонно, а при R > Z имеет знакопеременный характер.
Описанный режим используют в импульсной технике для формирования прямоугольных импульсов тока. Если условие согласования не выполнено, то переходный процесс состоит из бесконечного числа отражений волн на нагрузке и на входе. В этом случае при R > Z напряжение на нагрузке изменяется монотонно, а при R > Z имеет знакопеременный характер.
 , а на нагрузку подводится напряжение со всех его витков
, а на нагрузку подводится напряжение со всех его витков  .
Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной p, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы.
Центральным принципом решения переходного процесса операторным методом является преобразования обычной электрической схемы к операторной схеме замещения переменной p. Полученную схему рассчитывают любым известным методом (методом узловых потенциалов, контурных токов или эквивалентных преобразований например).
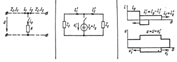
На рисунках ниже приведена схема электрической цепи и её операторная схема замещения соответственно:
.
Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной p, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы.
Центральным принципом решения переходного процесса операторным методом является преобразования обычной электрической схемы к операторной схеме замещения переменной p. Полученную схему рассчитывают любым известным методом (методом узловых потенциалов, контурных токов или эквивалентных преобразований например).
На рисунках ниже приведена схема электрической цепи и её операторная схема замещения соответственно:
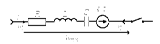
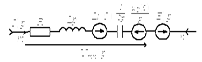 Таким образом правила преобразования основных элементов электрической цепи:
Активное сопротивление остаётся без изменений
Конденсатор ёмкостью C заменяется двумя элементами — конденсатором
Таким образом правила преобразования основных элементов электрической цепи:
Активное сопротивление остаётся без изменений
Конденсатор ёмкостью C заменяется двумя элементами — конденсатором 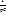 и источником ЭДС
и источником ЭДС 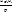 , который характеризует начальный заряд на конденсаторе
Индуктивность L заменяется двумя элементами — Индуктивностью pL и источником ЭДС L·iL(0), который характеризует начальный ток через индуктивность
Постоянный источник ЭДС или тока J, E заменяются на J/p и E/p соответственно
, который характеризует начальный заряд на конденсаторе
Индуктивность L заменяется двумя элементами — Индуктивностью pL и источником ЭДС L·iL(0), который характеризует начальный ток через индуктивность
Постоянный источник ЭДС или тока J, E заменяются на J/p и E/p соответственно