Гравитация и математический маятник

Для практического доказательства вращения гравитационных волн Солнца, необходимо их действие зафиксировать на Земле. Вращающееся поле Солнца должно периодически изменять гравитационное поле Земли, т.е. ускорение свободного падения. Самым простым методом определения ускорения свободного падения является математический маятник. Согласно теории [ 3,4 ],

Т = 2π· 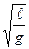, (5)

где Т – период свободных колебаний маятника [с];

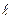- длина маятника [м];

g – ускорение свободного падения [м/с²].

Малые колебания математического маятника служат примером изохронных колебаний, т.е. колебаний, частота и периоды которых не зависят от амплитуды.

Опыты по фиксированию гравитационного поля Солнца проводились мною на конкретном математическом маятнике, подробные параметры которого представлены в Приложении 2 вместе со схемой маятника. По формуле (5) с помощью математического маятника можно определить только ускорение свободного падения в данной точке поверхности Земли. В таблице 1 /Приложение2/ даны средние значения периода колебаний Т_ср, определенные по десяти и ста колебаниям математического маятника. Подставив в формулу (5) значение Т_ср = 2,487 с и длину маятника 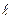= 1,537м, получим:

g = = [ ] = 9,81м/с². (6)
Точность определения ускорения свободного падения ограничивается изохронностью колебаний математического маятника. Поэтому для фиксирования гравитационного поля Солнца было решено определять потенциальную энергию маятника. Согласно теории [ 4 ], потенциальная энергия затухающих колебаний математического маятника напрямую зависит от амплитуды колебаний:

W_п = , (7) где W_п – потенциальная энергия маятника [Н·м];

k - коэффициент;

A - амплитуда [м].

Влияние гравитационного поля Солнца на потенциальную энергию и амплитуду затухающего математического маятника и легло в основу метода фиксирования гравитационных полей. Практическая часть заключалась в определении времени затухания колебаний маятника при постоянном значении интервала изменения амплитуды. Учитывая возможности конкретного математического маятника, были выбраны следующие две амплитуды А₀ = 70мм и А₁ = 5мм./Приложение 2/. Первые же опыты показали, что время затухания τ от запуска к запуску маятника может изменяться в широком диапазоне: от нескольких секунд до двух и более минут.

Суть проведения опытов заключалась в следующем: в течение 18 часов через каждые 15 минут запускался маятник и фиксировалось время затухания колебаний маятника с амплитуды А₀ = 70 мм до амплитуды А₁ = 5мм. В Приложении 3 на Рис.1 и Рис.2 представлены графики изменения времени затухания под действием гравитационных полей Солнца и Луны. На графиках минимальное время затухания τ₁ соответствует максимальному значению ускорения свободного падения на Земле, а максимальное τ₂ – минимальному ускорению.

В соответствии с теорией вращающихся гравитационных полей, период вращения поля Солнца составляет 166 мин., а Луны – 108 мин.[1]. Но на графиках эти периоды составили соответственно 210 мин. и 165 мин., т.е. период для Солнца увеличился в 1,27 раз, а для Луны – в 1,53 раза. На графиках они отмечены как земное время Т_земн. Увеличение периодов вращения полей Солнца и Луны связаны с вращением Земли вокруг своей оси и орбитальными движениями Земли и Луны. Гравитационное поле Солнца пересекает Землю по хорде, а отсчёт земного времени происходит по дуге земной окружности. В случае с Луной добавляется вращение последней вокруг Земли. Для Солнца участок активного взаимодействия полей охватывает на Земле угол в 105˚, а для Луны он составляет 82,5˚. Схемы взаимодействия гравитационных полей Солнца и Луны с полем Земли даны в Приложении 4.

На графиках, представленных в Приложении 3, видно как изменяется ускорение свободного падения на Земле в течение 18 часов под действием гравитационных полей Солнца и Луны. За время активной фазы Солнца и Луны их гравитационные поля успевают сделать по два оборота, т.е. проходит два периода. Активность фаз связана с тем, что в этот промежуток времени гравитационные поля Солнца и Луны движутся практически параллельно гравитационному полю Земли. Нарушение параллельности приводит к резкому снижению влияния полей Солнца и Луны на гравитационное поле Земли. На время активных фаз Солнца и Луны на Земле уменьшается ускорение свободного падения, как со светлой, так и с теневой сторон, т.к. на теневой стороне Земли гравитационные поля Солнца и Луны так же движутся практически параллельно гравитационному полю Земли.

Анализ графиков, представленных в Приложении 3, позволяет сделать следующие предварительные выводы:

1) С помощью математического маятника удалось зафиксировать гравитационные поля Солнца и Луны.

2) Вращающиеся гравитационные поля Солнца и Луны постоянно изменяют гравитацию на Земле.

3) Максимальное ослабление ускорения свободного падения на Земле происходит в активные фазы Солнца и Луны, когда их гравитационные поля проходят практически параллельно гравитационному полю Земли. Для Солнца эта зона охватывает 105˚ окружности Земли, а для Луны – 82,5˚, За время активной фазы гравитационные поля Солнца и Луны совершают по два оборота.

4) Нарушение параллельности полей приводит к резкому снижению влияния Солнца и Луны на гравитационное поле Земли.

5) Вращающиеся гравитационные поля Солнца и Луны снижают гравитационное поле Земли одновременно с светлой и теневой сторон Земли..

Графики, представленные на Рис.1 и Рис.2 в Приложении 3, свидетельствуют о существовании вращающихся гравитационных полей Солнца и Луны, но не позволяют количественно оценить их влияние на гравитационное поле Земли. Для количественной оценки необходимо определять изменение потенциальной энергии затухающего математического маятника.

Согласно теории [ 4 ], максимальная потенциальная энергия маятника определяется по формуле:

W_п = m·g·h, (8)

где W_п – максимальная потенциальная энергия [ Н· м];

m - масса грузика [кг];

g - ускорение свободного падения [м/с²];

h - высота положения грузика [м].

Для определения потенциальной энергии затухающего маятника применяется формула (7). В этой формуле коэффициент k зависит от величины действующего в данный момент ускорения свободного падения g. Этот коэффициент одновременно оказался характеристикой данного математического маятника [5]:

k = = 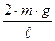, (9)

k - коэффициент математического маятника;

P - вес грузика маятника [кГ];

m - масса грузика маятника [кг ];

g - ускорение свободного падения [м/с²];

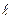- длина маятника [м].

Коэффициент k показывает отношение ускорения свободного падения на Земле на данный момент времени к ускорению свободного падения на Солнце[5]:

k = 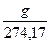. Для g = 9,81 м/с²; k = 0,03578. (10)
Каждому ускорению на Земле соответствует свой коэффициент k. При этом выполняется условие:

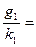
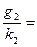274,17 м / с² (11)

где g₁,g₂ – ускорения свободного падения [м/с² ];

k_1,k₂ – соответствующие им коэффициенты;

274,17 – ускорение свободного падения на Солнце [ м/с² ].

Коэффициент k, как характеристика математического маятника, позволяет определить необходимое соотношение веса грузика маятника к его длине для получения «идеального» математического маятника. Чисто случайно конкретный математический маятник / приложение 2/ попал к разряд «идеальных»[4].

Для «идеального» затухающего математического маятника при постоянном ускорении свободного падения соблюдаются следующие соотношения[5]:

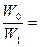
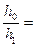
, (12)

где W – потенциальная энергия колебания маятника [Н· м];

h – высота положения грузика [м];

V – скорость прохождения нулевого положения [м/с];

A - амплитуда маятника [м].

Для затухающего математического маятника при изменении высоты грузика с h₀ до h₁ согласно формуле (8) можно записать: W₀ = m·g·h_0, а W₁= m·g·h₁. Разница потенциальных энергий ∆ W₀₁ = W₀ – W₁ даёт нам энергию выделенную маятником на участке ∆h = h₀ – h₁:

∆ W = m·g·∆h (13)
Аналогично рассуждая, при изменении амплитуды согласно формуле (7) получим:

∆W = ∆A² (14)
Разницу потенциальных энергий ∆W можно рассматривать, как работу совершаемую маятником на участке ∆h.

Согласно формуле (13 и 14) при постоянном значении g и Δ h или k и ∆А, потенциальная энергия маятника не должна изменяться, т.к. маятник за время колебаний τ совершает одинаковую работу. Но опыты показали, что два независимых колебания затухающего математического маятника при постоянном значении h и ∆А дают разное время затухания колебаний.

Это означает, что изменилась потенциальная энергия маятника. но изменение потенциальной энергии означает изменение гравитационного поля, т.е. ускорения свободного падения на Земле. Для сравнения двух независимых колебаний затухающего математического маятника можно записать[5]:

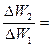
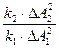= . (15)
В формуле (15) τ₁ и τ₂ – время затухания двух независимых колебаний. Величина τ₂ соответствует среднеарифметическому значению времени затухания замеренных колебаний маятника для активной фазы Солнца, а величина τ₁ – для участков, где ни Солнце, ни Луна практически не влияли на гравитационное поле Земли. Минимальное среднее значение τ₁ = 627,7с, а максимальное значение τ₂ = 771,1с. Величина ∆W₁ в равенстве (15) соответствует значению ∆ W = 8,7295·10^-5 Н·м определенной для g = 9,81 м/с² /Приложение 2/. Величину ∆W₂ для нового значения g₂ при τ₂ = 771,1с можно определить из равенства (15):

∆W₂ = = [ 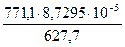] = 1,0724·10⁻⁴ Н·м. (16)
Разность потенциальных энергий двух независимых затухающих колебаний ∆W₁₂ =

=∆W_₂ -∆W_₁ = [1,0724·10^-4 – 8,7295·10^-5]= 1,9945·10^-5 Н·м. Эта разность потенциальных энергий математического маятника соответствует изменению

∆g = g₁ - g₂ = 9,81 – g₂.
Величина g₂ - ускорение свободного падения на Земле при активной фазе Солнца. Но равенство (15) не имеет однозначного решения относительно g₂ и ∆h₂, т.к. эти величины взаимозависимы. По этой же причине невозможно однозначно определить k и ∆А₂.

В связи с этим для определения g₂ был применён метод последовательного изменения коэффициента k[4]. Он одновременно является параметром математического маятника и однозначно определяется по формуле (9). Для ускорения g₁ = 9,81 м/с² коэффициент k₁ = 0,03578, при этом с уменьшением g коэффициент k также уменьшается.

В Таблице 1 даны значения четырёх коэффициентов k с шагом 0,00001. Таблица 1

∆W' =
№ k ∆ k g ∆g ∆W ∆W₂ - ∆W₁

[м / с²] [м / с²] [Н · м ] [Н · м]

1. 0,03578 0,0 9,8098 0,0 8,7295·10^-5 0,0

2. 0,03577 0,00001 9,8071 0,00274 - -

3. 0,03576 0,00002 9,8043 0,00548 1,0724·10^-4 0,00002

4. 0,03575 0,00003 9,8016 0,00822 - -

Примечание. Величина g рассчитана по формуле (6).

В таблице 1 условиям опыта с затухающими колебаниями математического маятника соответствуют первая и третья строки. Коэффициент k₁ и g₁ – исходные параметры опыта. Первая строка соответствует параметрам, полученным при τ₁, а третья срока – при τ₂. Для коэффициента k = 0,03576 /при τ₂/ величина ∆g = 0,00548 м/c² лучше всех согласуется со средней величиной ускорения Солнца на орбите Земли, которая, как известно, равняется 0,00593 м/с². С учетом апогея и перигея Земли оно может колебаться от 0,00575 м/с² до 0,00614 м/с²[3,4].Но, согласно условиям проведения опыта, время затухания маятника τ₂ соответствует как раз активной фазе Солнца. Для коэффициента k= = 0,03575 величина ∆ g = 0,0082 м/с², что значительно превышает максимальное ускорение для Солнца на орбите Земли, равного 0,00614 м/с². Это означает, что коэффициент k = 0,03575 уже не связан с гравитацией Солнца.

Анализ Таблицы 1 показал, что между величинами ∆k, ∆g и разницей потенциальных энергий ∆W₁₂= ∆W₂ - ∆W₁ имеется чёткая зависимость[5]:

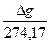= ∆k = - ∆W₁₂ . (17)
Знак минус при ∆W₁₂ означает, что при увеличении g и k потенциальная энергия
∆W₁₂ уменьшается. Формула (17) позволяет по разности потенциальной энергии затухающего математического маятника определить величину изменения ускорения свободного падения на Земле ∆g.

Согласно условиям опыта, определялось время затухания колебаний маятника τ₁ и τ₂, которые соответствовали минимальной и максимальной фазе Солнца.
Для τ₁ = 627,7с по формуле (6) определялось ускорение свободного падения g = 9,81 м/с², а по формуле (13) определялась потенциальная энергия ∆W₁ = 8,7295·10^-5 Н·м. Для τ₂ = 771,1с потенциальная энергия определялась по формуле (16) ∆W₂ = =1,0724·10^-4 Н·м. Величина изменения ускорения свободного падения на Земле под действием гравитационного поля Солнца ∆g определялась по формуле (17), где ∆W₁₂=∆W₂ - ∆W₁ = [1,0724·10^-4 – 8,7295·10^-5]= 1,9945·10^-5 Н·м;

∆g = [274,17·(-1,9945·10^-5)]=- 5,4683·10^-3 м/с².

Гравитационное поле Солнца уменьшает гравитационное поле Земли на 0,00547 м/с² в период активной фазы Солнца. Эта величина соответствует ускорению свободного падения для Солнца на орбите Земли.

Таким образом, с помощью затухающего математического маятника удалось не только показать влияние гравитационного поля Солнца на земное ускорение, но и определить количественно его величину.

С помощью формулы (17) можно, например, определить потенциальную энергию при коэффициенте k = 0,03577, которому соответствует промежуточная энергия между ∆W₁ и ∆W₂. Для данного коэффициента, согласно Таблицы 1, ∆k = 0,00001, и согласно формуле (17) ∆ W₁₂ = 0,00001 Н·м. Промежуточная потенциальная энергия ∆W_пр = ∆W₁ + ∆W₁₂ =[ 8,7295·10^-5 + 1,0·10^-5]= 9,7295^-5 Н·м. Для ∆W_пр по формуле (15) можно определить значение время затухания маятника τ_пр, которое должно соответствовать промежуточному времени затухания маятника между τ₁ и τ₂:

τ_пр = = [ 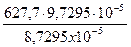]= 699,6 с (18)
Величина τ_пр является среднеарифметическим значением для τ₁ и τ₂. Этот пример можно считать подтверждением того, что разница потенциальных энергий ∆W₂ - ∆W₁ =0,00002 Н·м действительно соответствует коэффициенту k = 0,03576, при котором ∆g является ускорением свободного падения Солнца на орбите Земли.

Подводя итоги количественной части опыта можно сделать следующие выводы:

1) Определена величина изменения ускорения свободного падения для Земли во время активной фазы Солнца, равная 0,00547 м/с².

2) Определена зависимость между изменением потенциальной энергии
затухающего математического маятника ∆W, изменением коэффициента ∆ k и изменением ускорения свободного падения на Земле ∆g.
3) При максимальной фазе Солнца ускорение свободного падения на Земле уменьшается на величину ускорения свободного падения для Солнца на орбите Земли.

Заключение

Простой анализ единицы измерения гравитационного потенциала позволил открыть в Космосе вращающиеся гравитационные поля, которые привели к открытию гравитационной массы. Вращающиеся гравитационные поля и гравитационная масса позволяют получить ответ на многие проблемы физики Космоса, которые ждут решения не одно десятилетие и даже столетие:

1) Скорость света – это линейная скорость вращения гравитационного поля ядра нашей Галактики и скорость распространения сферической гравитационной волны ядра Галактики, которые равны 2,9979·10⁸ м/с.

2) Гравитационная постоянная - это угловая скорость вращения гравитационного поля ядра нашей Галактики равная 6,672·10⁻¹¹ рад/с. На Земле она измеряется в [м³/кг с²].

3) Все космические тела обладают своими вращающимися гравитационными полями, которые через их плотность задаются гравитационным полем ядра Галактики.

4) Вращающиеся гравитационные поля Солнца и Луны удалось зафиксировать с помощью затухающего математического маятника и количественно определить влияние гравитации Солнца на ускорение свободного падения на Земле.

5) В Космосе действуют только центростремительные ускорения, т.к. угловые скорости вращения полей составляют тысячные и даже миллиардные доли рад/с, а сами космические тела вращаются еще медленнее.

6) Центростремительные ускорения вращающихся гравитационных полей в Космосе и являются источником Всемирного притяжения.

7) Масса гравитационного поля космического тела составляет от десяти до ста миллионных долей массы вещества тела. Но именно гравитационное поле и создает гравитацию космического тела. В космических системах, таких как солнечная, галактическая и Вселенная, соотношение масс поля и вещества противоположное. Здесь уже масса вещества может составлять миллионные и триллионные доли массы гравитационного поля системы.

8) «Тёмная материя» в Космосе – это гравитационная масса вращающихся полей космических объектов: планет, звезд, галактик и Вселенной.

Сегодня теория вращающихся гравитационных полей в Космосе и их гравитационных масс не принимается классическими физиками и астрофизиками, несмотря на то, что она позволяет решить многие проблемы в Космосе и даже заглянуть в Атом. Автор рассчитывает, что современные студенты и молодые учёные, которым предстоит создавать науку XXI-ХХII веков, непременно продолжат развитие этих идей и откроют новые законы Природы как в мире Космоса, так и в мире Атома.

Литература.

1. В.Н.Макаров. О гипотезе вращающейся гравитации во Вселенной//. «Вселенная и жизнь», Сборник НКЛФА, Нижний Новгород. 2010,с.55-59.

2. И.А.Климишин. Астрономия наших дней. М.Наука,1986,559 с.

3. Б.М.Яворский, А.А.Детлаф. Физика для школьников старших классов и поступающих в вузы. М, Дрофа, 2005, 795 с.

4. И.Л.Касаткина. Репетитор по физике. Теория. Ростов на Дону, Феникс, 2003, 443с.

5. В.Н.Макаров. Природа гравитации и арифметика Космоса.// «Вселенная и жизнь», Сборник НКЛФА, Нижний Новгород 2013,с.24-37.

Приложение 1

Дата добавления: 2015-05-06