Основные теоретические положения. Если к зажимам электрической цепи (рис.1), состоящей из параллельно соединенных катушки индуктивности (с активным сопротивлением Rк и индуктивностью L) и

Если к зажимам электрической цепи (рис.1), состоящей из параллельно соединенных катушки индуктивности (с активным сопротивлением R_к и индуктивностью L) и конденсатором (емкостью С), приложено напряжение, меняющееся во времени по синусоидальному закону u (t) = U_m sin wt, то токи в параллельных ветвях и неразветвленной части цепи также будут синусоидальными:

i_к (t) = 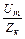sin (wt - j_к) = I_mк sin (wt - j_к);

i_с (t) = sin (wt + j_c) = I_mc sin (wt + j_c);

i (t) = i _к (t) + i _с (t),

где X_с = - сопротивление батареи конденсаторов;

X_к = wL_к - индуктивное сопротивление катушки;

Z_к = 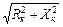- полное сопротивление катушки индуктивности;

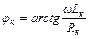; ; w = 2 pf;

f – частота синусоидального тока.

Рис. 1

По закону Ома в комплексной форме ток в катушке равен:

= = = =

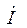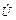
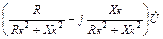= (g_к – j b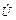_к) = Y _к = ,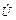

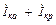где Y _к = g_к – j b_к - комплекс полной проводимости катушки;

- активная проводимость катушки;

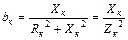- индуктивная проводимость катушки;

g_к 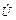- активная составляющая тока катушки, совпадающая по фазе с напряжением Ú;

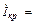– j b_к 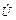- реактивная составляющая тока катушки, отстающая по фазе от напряжения 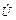на p /2.

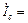
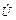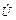Ток в ветви с конденсатором равен: = = jwС = jb_c .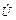

Ток в неразветвленной части цепи определяется формулой

=

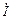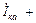
или 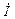= [ g_к – j (b_к – b_c)] 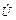= Y ,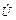

где Y = g_к – j (b_к – b_c) = ye^-jj = y cos j + jy sin j - комплекс полной проводимости всей цепи (рис.1); j = arctg - угол между напряжением U, приложенным ко всей цепи, и током в неразветвленной части цепи I; y = 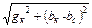- модуль полной проводимости цепи;

Векторная диаграмма токов (рис.2) строится на основании уравнения, составленного по первому закону Кирхгофа. Начальную фазу напряжения 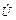принимают равной нулю, то есть 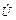= U, вектор напряжения 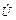совмещается с осью +1 на комплексной плоскости.

На рис.2 приведена векторная диаграмма для случая, когда b_c > b_к (после резонанса) и напряжение 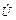отстает по фазе от тока на угол j < p /2. Ток в неразветвленной части цепи носит активно-емкостной характер (I_c > I_кр).

Рис.2 Рис.3

Резонансом тока называют явление в параллельной цепи с емкостными и индуктивными приемниками, когда общий ток в неразветвленной части цепи и напряжение на входе цепи совпадают по фазе. Резонанс токов характеризуется равенством реактивных токов в индуктивном и емкостном приемниках. Ток в неразветвленной части цепи минимальный, совпадает по фазе с напряжением и определяется активными составляющими токов емкостного и индуктивного приемников. Для цепи, представленной на рис.1, резонансное состояние характеризуется соотношениями:

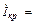
, , j = 0.

Векторная диаграмма для резонансного режима представлена на рис.3.

Ток в неразветвленной части цепи определяется выражением

I = y 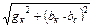U = U.

Поскольку при резонансе ток в неразветвленной части цепи чисто активный, то условием резонанса является равенство реактивных проводимостей приемников:

b_к = b_с или + w ₀² L_к ² = w ₀ C.

Это условие называется условием резонанса токов. Резонансное состояние можно получить, изменяя параметры цепи С, L_к, R_к или частоту напряжения сети w.

Резонансная частота f ₀ = w ₀ / 2 p определяется из условия резонанса

f ₀= .

Видно, что резонанс возможен лишь при условии >R_к. При резонансе ток в цепи I минимален: I = gU.

Реактивные токи в приемниках могут оказаться больше активного тока в неразветвленной части цепи. Превышение реактивных токов приемников при резонансе по сравнению с активным током в неразветвленной части цепи характеризуют добротностью цепи q.

На рис. 3 показана векторная диаграмма токов для контура в режиме резонанса. В этом режиме входной ток достигает максимального значения и его амплитудное значение равно I_0m = U_1m/R. Если R является активным сопротивлением проводов катушки, то мощность

P = 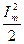Rучитывает активные потери мощности в ней. Потери мощности в конденсаторе для низких и средних частот составляют малую величину и в его схеме замещения не учитываются.

Амплитудные значения токов на реактивных элементах L и C в режиме резонанса могут значительно превышать входное напряжение

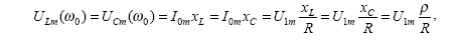(4)

где r - характеристическое сопротивление последовательного колебательного конура

(5)

Отношение Q = r/R - называется добротностью контура. Для контуров, применяемых в радиоэлектронике, величина Q достигает десятков и сотен единиц.

С целью оценки уровня искажения сигналов для колебательного контура используют понятие полосы пропускания (П). Полосой пропускания контура называют диапазон частот, в котором АЧХ уменьшается не более, чем в 2 раз по сравнению с ее значением при резонансной частоте, что соответствует на ЛАЧХ уменьшению характеристики на –3 дБ (рис. 5,а). Полоса пропускания контура П=ω_Г2 - ω_Г1, где ω_Г1 и ω_Г2- граничные частоты полосы пропускания..

Мгновенная мощность в цепи есть произведение мгновенных значений тока и напряжения р (t) = u (t) i (t).

Активная мощность – среднее за период значение мгновенной мощности, то есть активная мощность характеризует среднюю мощность преобразования энергии в цепи в другие виды энергии:

P = 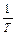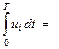UI cos j.

При параллельном соединении

P = UI_a = U ² g,

где U и I – соответственно действующие значения напряжения и тока в цепи;

j - угол сдвига по фазе между током и напряжением в цепи, зависит от характера нагрузки; g - активная проводимость цепи.

Полная мощность цепи – мощность, подводимая к зажимам цепи и характеризующая амплитуду колебаний мощности в цепи. Определяют полную мощность произведением действующих значений тока и напряжения

S = UI.

Реактивная мощность цепи – мощность, периодически запасаемая в реактивных элементах и отдаваемая ими обратно генератору, равная:

Q = UI sin j.

Комплексная форма полной мощности

= Scos j + jS sin j = P + jQ

дает возможность построить векторную диаграмму мощностей – треугольник мощностей (рис.4). Из векторной диаграммы мощностей находим полную мощность: S =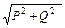

При резонансе реактивная мощность цепи Q = 0. Реактивные мощности на участках цепи с L_к и C характеризуют взаимное преобразование энергии электрического и магнитного полей индуктивности и емкости. Активная мощность P = S.

Резонанс токов используют в установках для повышения коэффициента мощности, подключая параллельно приемнику с сосредоточенными параметрами R, L конденсаторную батарею емкостью С:

C = I_c / 2 pfU = I_к sin j_к / 2 pfU,

которая обеспечивает полную компенсацию сдвига фаз между напряжением U и током I, при этом коэффициент мощности cos j = 1 и источник электрической энергии полностью разгружается от реактивного тока (S = P). Обычно коэффициент мощности установок доводят до 0,9…0,95. Еще большее повышение cos j требует больших затрат на установку батарей конденсаторов, которые экономически не оправдываются. В этом случае емкость батареи конденсаторов определяется формулой

C = (P / 2 pfU ²)(tg j_н - tg j),

где P - активная мощность приемника; j_н - угол сдвига по фазе приемника; j - требуемый угол сдвига по фазе.

Повышение коэффициента мощности установок снижает ток в линии электропередач, потери в линии DP_л = I ² R_л.

Порядок выполнения работы

Экспериментальное исследование линейной разветвленной электрической цепи синусоидального тока выполняют на установке, схема которой приведена на рис.5. Цепь состоит из параллельно соединенных индуктивной катушки L и конденсатора С.

Для измерения комплекса амплитудного значения тока Im и комплексного входного сопротивления -

необходимо воспользоваться комбинированным прибором измерителя мощности и фазы (ИМФ1). Он позволяет проводить измерения амплитудных значений синусоидального тока и падения напряжения на участке исследуемой цепи, а также разности фаз между током и напряжением. Измерительная схема представлена на рис. 5.

Для определения комплекса амплитудного значения напряжения на элементе Z2 (U _Rm, U _Lm и U_Cm), комплексной передаточной функции по напряжению использовать комбинированный прибор измерения мощности и фазы (ИМФ1). Он позволяет проводить измерения амплитудных значений падений напряжения на участках исследуемой цепи, а также разности фаз между ними. Измерительная схема представлена на рис. 5.

Рис.5

Задание к работе

1. Собрать схему по рис 5. В качестве исследуемой цепи, входным сопротивлением Z соберите схему рис. 1. Для этой схемы номиналы элементов R, L и C должны соответствовать значениям, выбранных при расчетах. Установить амплитуду напряжения генератора U₁ = 2B.

Определить резонансную частоту f₀. Для этого плавно изменяя частоту генератора f от 1000 до 15000 Гц необходимо получить разность фаз входного напряжения и – φ = 0 (показание ИМФ1 в режиме измерения фазы между напряжением и током). При этом ток в неразветвленной части цепи достигает минимальной величины (показание ИМФ1 в режиме измерения тока). Задавая частоту генератора f = 1000, f₀, 15000 Гц, измерить с помощью ИМФ1 измерения комплекса амплитудного значения тока Im и комплексного входного сопротивления Z. Результаты измерений занести в табл. 2.

2. Изменяя частоту генератора f от 1000 до 15000 Гц с шагом 1000 Гц измерить токи I, I_c, I_к, подключая прибор АВ вместо перемычек П1 и П2, разность фаз j, а также cosj. Результаты занести в таблицу 1.По данным эксперимента (табл. 1) для схемы рис 1 рассчитать и построить графики I_c (f), I_к (f), cosj = f (f).

3. По экспериментальным данным определить добротность контура - Q, характеристическое сопротивление - r и граничные частоты полосы пропускания контура - f_Г1 и f_Г2. Отметить на графиках граничные частоты и полосу пропускания.

4. По данным эксперимента, снятым для частот f = 1000, f₀ и 15000 Гц (табл. 1, схема рис 1), построить векторные диаграммы токов и напряжений.

Указание: При построении векторной диаграммы нужно помнить, что I_С = I_L, только тогда, когда R_к » 0.

В нашем опыте R_к ¹ 0, поэтому 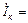, где I_ка и I_кр – активная и реактивная составляющие тока катушки; I_ка = g_кU; I_кр = b_кU или (см. рис.2): I_ка =I_к cos j_к; I_кр = I_к sin j_к = 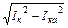; cos j_к = .

Так как активная мощность выделяется только на катушке, то показание ваттметра ИМФ1 и есть мощность катушки P_к.

Отсюда P = P_к = UI cos j = UI_к cos j_к = UI_ка = g_кU ² = R_кI _к ².

Построение векторной диаграммы токов и напряжений можно проводить так (рис.2):

1. Совместить вектор 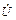с действительной осью;

2. Под углом j_к отложить вектор = I_к e^-jjк;

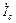3. От вектора провести вектор , опережающий напряжение на угол p /2;

4. Замыкающий вектор = + .

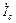По этим данным рассчитываются параметры катушки:

Z_к = U/ I_к, R_к = P/ I _к ², X_к = , L_к = X_к / 2 pf, f = 50 Гц.

Для конденсатора известно U, I_c. Отсюда X_c = U/ I_c, b_c = I_c / U.

Таблица 1

Данные наблюдений

Результаты вычислений

№

f,Гц

U, В

I, А

Iс , А

Iк , А

P, Вт

S, ВА

Q, ВАр

cosj

y, См ^-^1

qк , Ом^- ^1

bк, Ом^- ^1

bc, Ом^- ^1

xc, Ом

q

1…3

Таблица 2

f,Гц	Результаты вычислений
Zк	Rк	Xк	cos jк	Lк	gк

Вопросы для самоконтроля

1. Как определить полное сопротивление ветви электрической цепи синусоидального тока?

2. Какие величины определяют знак реактивного сопротивления ветви той же электрической цепи?

3. Как рассчитать ток в неразветвленной части электрической цепи синусоидального тока?

4. В какой электрической цепи и при каких условиях может возникнуть резонанс токов?

5. Чему равен коэффициент мощности цепи при резонансе токов?

6. Могут ли действующие токи в ветвях электрической цепи превышать действующий ток в неразветвленной части этой же цепи?

7. Чему равна реактивная мощность в цепи при резонансе токов?

Список литературы

1. Электротехника и электроника: учебное пособие для вузов/ В.В. Кононенко и др.Ростов н/Д: Феникс, 2008.

2. Жаворонков М.А. Электротехника и электроника: учеб. Пособие для студ. Высш. Учеб. Заведений/ М.А. Жаворонков, А.В. Кузин.-М.: Издательский центр «Академия», 2010.

3. Данилов И.А., Иванов П.М. Общая электротехника с основами электроники: Учеб. Пособие.- М.: Высшая школа, 2000.

Лабораторная работа №5

Дата добавления: 2015-05-06