
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частотные свойства биполярного транзистора
|
|
|
|
ЧАСТОТНЫЕ СВОЙСТВА И ПЕРЕХОДНЫЕ ПРОЦЕССЫ В БИПОЛЯРНОМ ТРАНЗИСТОРЕ
Рассмотрим поведение п-р-п транзистора, включённого в схеме с ОБ и работающего в режиме класса А, когда на его входе действует переменный ток 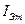 . Пусть амплитуда тока остаётся постоянной, а его частота w меняется в широких пределах. При этом можно увидеть, что с увеличением частоты входного тока
. Пусть амплитуда тока остаётся постоянной, а его частота w меняется в широких пределах. При этом можно увидеть, что с увеличением частоты входного тока 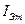 , переменная составляющая выходного тока
, переменная составляющая выходного тока 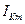 начинает запаздывать по фазе, а его амплитуда уменьшается. Это говорит о том, что появляется частотная зависимость комплексного коэффициента передачи тока
начинает запаздывать по фазе, а его амплитуда уменьшается. Это говорит о том, что появляется частотная зависимость комплексного коэффициента передачи тока 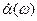 .
.
Как известно из (3.9), 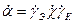 , где
, где 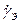 – коэффициент инжекции эмиттера,
– коэффициент инжекции эмиттера, 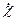 – коэффициент переноса носителей через базу,
– коэффициент переноса носителей через базу, 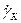 – коэффициент экстракции носителей тока коллекторным переходом. Отсюда вытекает, что зависимость
– коэффициент экстракции носителей тока коллекторным переходом. Отсюда вытекает, что зависимость 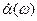 распадается на зависимости
распадается на зависимости 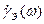 ,
, 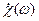 и
и 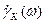 .
.
Частотная зависимость коэффициента инжекции 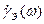 обусловлена наличием барьерной СЭбар и диффузионной СЭ.диф емкостей эмиттерного перехода, шунтирующих дифференциальное сопротивление rЭ эмиттерного перехода. Эквивалентная схема цепи эмиттера представлена на рис.7.1.
обусловлена наличием барьерной СЭбар и диффузионной СЭ.диф емкостей эмиттерного перехода, шунтирующих дифференциальное сопротивление rЭ эмиттерного перехода. Эквивалентная схема цепи эмиттера представлена на рис.7.1.
 Из эквивалентной схемы следует, что переменный ток эмиттерного перехода определяется суммой токов, протекающих через дифференциальное сопротивление и емкости эмиттерного перехода. При этом часть тока эмиттера, протекающая через дифференциальное сопротивление
Из эквивалентной схемы следует, что переменный ток эмиттерного перехода определяется суммой токов, протекающих через дифференциальное сопротивление и емкости эмиттерного перехода. При этом часть тока эмиттера, протекающая через дифференциальное сопротивление
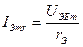 (7.1)
(7.1)
|
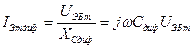 , (7.2)
, (7.2)
определяет инжекцию неосновных носителей в базу, а ток через барьерную емкость 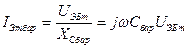 (7.3)
(7.3)
не связана с инжекцией. В выражениях (7.1)-(7.3) 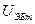 - переменная составляющая напряжения на эмиттерном переходе.
- переменная составляющая напряжения на эмиттерном переходе.
В соответствие с (3.3) и с учетом (7.1)-(7.3) для коэффициента инжекции имеем:
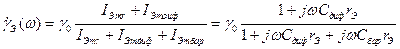 , (7.4)
, (7.4)
где 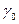 - коэффициент инжекции по постоянному току. Для упрощения (7.4) учтем, что на рабочих частотах для биполярного транзистора обычно выполняется
- коэффициент инжекции по постоянному току. Для упрощения (7.4) учтем, что на рабочих частотах для биполярного транзистора обычно выполняется 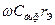 <<1 и
<<1 и 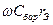 <<1. В этом случае знаменатель в (7.4) можно представить в виде
<<1. В этом случае знаменатель в (7.4) можно представить в виде 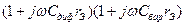 , так как после раскрытия скобок можно пренебречь произведением двух малых величин. Тогда (7.4) можно записать в виде
, так как после раскрытия скобок можно пренебречь произведением двух малых величин. Тогда (7.4) можно записать в виде
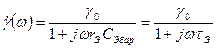 , (7.5)
, (7.5)
где 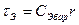 (7.6)
(7.6)
– называется постоянной времени эмиттерного перехода, определяемая процессами перезарядки CЭ.бар и она характеризует время задержки тока эмиттера на эмиттерном переходе. Выражение (7.5) показывает, что с увеличением частоты из–за шунтирующего действия барьерной ёмкости эмиттера доля инжектированных носителей заряда уменьшается, а также возникает сдвиг фазы между входным током и током инжектированных в базу носителей за счет времени задержки (7.6).
Основной вклад в частотную зависимость 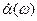 вносит зависимость
вносит зависимость 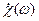 , обусловленная диффузионным переносом неосновных носителей заряда через базу. Влияние частоты на коэффициент переноса возникает на частотах входного сигнала, когда период сигнала
, обусловленная диффузионным переносом неосновных носителей заряда через базу. Влияние частоты на коэффициент переноса возникает на частотах входного сигнала, когда период сигнала 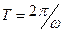 становится сравнимой со временем пролета электронов через базу. В этом случае до коллектора за половину периода сигнала, вызывающего инжекцию электронов в базу, успевают дойти только наиболее быстрые электроны. При изменении полярности входного сигнала не дошедшие до коллектора медленные электроны изменяют свое направление и двигаются к эмиттеру. Это приводит к уменьшению тока коллектора, т.е появляется зависимость коэффициента переноса от частоты сигнала.
становится сравнимой со временем пролета электронов через базу. В этом случае до коллектора за половину периода сигнала, вызывающего инжекцию электронов в базу, успевают дойти только наиболее быстрые электроны. При изменении полярности входного сигнала не дошедшие до коллектора медленные электроны изменяют свое направление и двигаются к эмиттеру. Это приводит к уменьшению тока коллектора, т.е появляется зависимость коэффициента переноса от частоты сигнала.
Решение уравнения диффузии для бездрейфового транзистора при условии, что ширина базы d постоянна и намного меньше длины диффузионного смещения электронов lDп (d<<lDп,) дает, что зависимость коэффициента переноса от частоты сигнала определяется выражением:
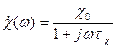 , (7.7)
, (7.7)
где 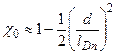 (7.8)
(7.8)
– коэффициент переноса на низкой частоте (см.также (3.6)), tc – время переноса электронов через базу, определяемая формулой
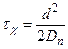 . (7.9)
. (7.9)
В (7.9) Dn – коэффициент диффузии электронов.
Из выражения (7.7) следует, что с увеличением частоты сигнала 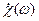 уменьшается и появляется запаздывание сигнала, обусловленное временем tc.
уменьшается и появляется запаздывание сигнала, обусловленное временем tc.
Частотная зависимость коэффициента экстракции носителей тока коллекторным переходом определяется двумя факторами: временем пролёта tпр через область объёмного заряда коллекторного перехода и постоянной времени цепи коллектора tK, обусловленный барьерной емкостью коллекторного перехода. Таким образом, 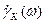 можно представить в виде произведения двух составляющих
можно представить в виде произведения двух составляющих 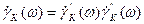 , определяемые этими факторами.
, определяемые этими факторами.
При движении электронов через объёмный заряд коллекторного перехода в последнем наводится ток. Расчет наведённого тока при воздействии гармонического сигнала показывает, что ток через переход изменяется как по амплитуде, так и по фазе. Для коэффициента переноса 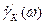 через переход можно получить:
через переход можно получить:
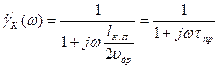 , (7.10)
, (7.10)
где 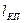 - ширина коллекторного перехода,
- ширина коллекторного перехода, 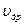 – скорость дрейфа электронов в поле объемного заряда коллекторного перехода шириной, которая приблизительно равна средней тепловой скорости и
– скорость дрейфа электронов в поле объемного заряда коллекторного перехода шириной, которая приблизительно равна средней тепловой скорости и
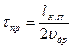 (7.11)
(7.11)
время пролета электронов в коллекторном переходе.
Коллектор реального транзистора характеризуется некоторым объёмным сопротивлением Rk (см. рис.4.3), поэтому процессы переноса заряда в коллекторе характеризуются постоянной времени цепи коллектора:
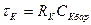 , (7.12)
, (7.12)
где CК.бар –барьерная ёмкость цепи коллектора. При воздействии гармонического сигнала за счет 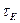 возникает, аналогично эмиттерному переходу, зависимость коэффициента переноса тока через коллекторный переход от частоты:
возникает, аналогично эмиттерному переходу, зависимость коэффициента переноса тока через коллекторный переход от частоты:
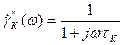 . (7.13)
. (7.13)
Выражения (7.10) и (7.13) показывают, что с увеличением частоты коэффициент 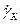 уменьшается.
уменьшается.
Учитывая все рассмотренные факторы, влияющие на частотные свойства транзистора, коэффициент передачи тока можно аппроксимировать выражением
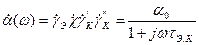 , (7.14)
, (7.14)
где a0 –коэффициент передачи тока на низкой частоте,
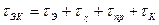 , (7.15)
, (7.15)
полная постоянная времени транзистора в схеме с ОБ, определяющая временную задержку тока коллектора от тока эмиттера (рис.7.2).
При работе транзистора в схеме с ОЭ частотную зависимость коэффициента передачи тока эмиттера 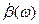 с учетом, что
с учетом, что 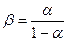 можно представить в виде выражения, аналогичного (7.14):
можно представить в виде выражения, аналогичного (7.14):

|
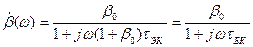 , (7.16)
, (7.16)
где b0 - коэффициент передачи тока базы на низкой частоте, 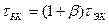 - постоянная времени транзистора в схеме с ОЭ.
- постоянная времени транзистора в схеме с ОЭ.
На основе (7.14) и (7.16) определим модули и фазовые угли коэффициентов передачи тока:
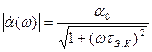 и
и 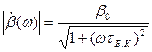 , (7.17)
, (7.17)
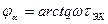 и
и 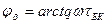 . (7.18)
. (7.18)
Графики частотных зависимостей, построенные на основе (7.17) приведены на рисунке 7.3.
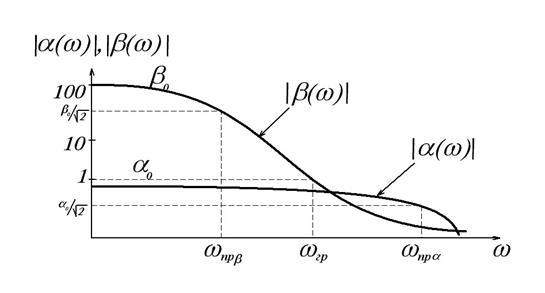
Рис. 7.3. Частотные зависимости коэффициентов передачи тока.
Из графических зависимостей можно определить основные частотные параметры биполярного транзистора. К таким параметрам относятся:
1. Предельная частота транзистора в схеме с ОБ 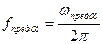 , определяемая как частота, на которой коэффициент передачи тока эмиттера
, определяемая как частота, на которой коэффициент передачи тока эмиттера 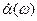 уменьшается в
уменьшается в 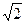 раз по сравнению на низкой частоте(см.рис.7.3);
раз по сравнению на низкой частоте(см.рис.7.3);
2. Предельная частота транзистора в схеме с ОЭ 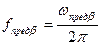 ,
,
определяемая как частота, на которой коэффициент передачи тока базы 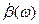 уменьшается в
уменьшается в 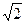 раз по сравнению на низкой частоте (см.рис.7.3);
раз по сравнению на низкой частоте (см.рис.7.3);
3. Граничная частота транзистора в схеме с ОЭ 
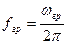 , определяемая как частота, на которой коэффициент передачи тока базы уменьшается до единицы, т.е частота, на которой
, определяемая как частота, на которой коэффициент передачи тока базы уменьшается до единицы, т.е частота, на которой 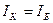 (см.рис.7.3).
(см.рис.7.3).
4. Максимальная частота 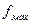 , определяемая как частота, на которой коэффициент усиления по мощности становится равной единице. Максимальная частота определяет область частот, в которой транзистор остается активным элементом электрической схемы, так как транзистор можно использовать в усилительных схемах только в том случае, если его коэффициент усиления по мощности КР > 1. Расчеты показывают, что
, определяемая как частота, на которой коэффициент усиления по мощности становится равной единице. Максимальная частота определяет область частот, в которой транзистор остается активным элементом электрической схемы, так как транзистор можно использовать в усилительных схемах только в том случае, если его коэффициент усиления по мощности КР > 1. Расчеты показывают, что 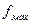 определяется формулой
определяется формулой
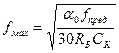 , (7.19)
, (7.19)
где RБ – объемное сопротивление базовой области (см. рис.4.3). Произведение 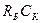 называют постоянной времени цепи обратной связи, которая характеризует обратную связь на высокой частоте и является также параметром транзистора.
называют постоянной времени цепи обратной связи, которая характеризует обратную связь на высокой частоте и является также параметром транзистора.
Из (7.17) вытекает, что 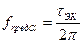 и
и 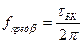 (7.20)
(7.20)
С учетом(7.20) (7.17) примет вид
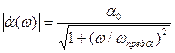 и
и  (7.21)
(7.21)
Как видно из рисунка 7.3, 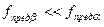 . Учитывая (7.16), можно получить, что
. Учитывая (7.16), можно получить, что 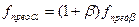 . Физически это неравенство связано с влиянием фазового сдвига j между токами эмиттера и коллектора, определяемого как
. Физически это неравенство связано с влиянием фазового сдвига j между токами эмиттера и коллектора, определяемого как 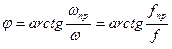 . Действительно, с увеличением частоты фазовый сдвиг между током коллектора и током базы растёт, что приводит уменьшению тока коллектора и росту тока базы (рис.7.4). Отсюда вытекает, что если даже токи
. Действительно, с увеличением частоты фазовый сдвиг между током коллектора и током базы растёт, что приводит уменьшению тока коллектора и росту тока базы (рис.7.4). Отсюда вытекает, что если даже токи
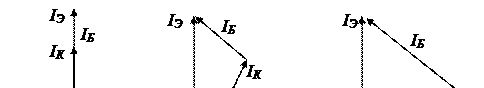
Рис.7.4. Векторные диаграммы токов транзистора на разных частотах
эмиттера и коллектора остаются неизменными по абсолютной величине, т.е 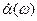 практически не меняется, но
практически не меняется, но 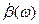 уменьшается значительно за счет роста тока базы. С физической точки зрения рост тока базы вызывается тем, что с ростом частоты инжектированные из эмиттера электроны, не успевают дойти до коллекторного перехода и рекомбинируют с дырками в области базы, увеличивая рекомбинационную составляющую тока базы.
уменьшается значительно за счет роста тока базы. С физической точки зрения рост тока базы вызывается тем, что с ростом частоты инжектированные из эмиттера электроны, не успевают дойти до коллекторного перехода и рекомбинируют с дырками в области базы, увеличивая рекомбинационную составляющую тока базы.
|
|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 2045; Нарушение авторских прав?; Мы поможем в написании вашей работы!