
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Постоянный ток(напряжение). Переменный ток(напряжение). Гармоническое колебание как частный случай переменного тока(напряжения). Векторное представление
|
|
|
|
Характеристики тока. Мгновенное, амплитудное, среднее и действующее значение.


Большинство измерительных приборов показывает действующее значение измеряемой величины.
Коэффициент амплитуды и коэффициент формы.
 Коэффициент амплитуды (пикфактор сигнала) – это отношение ампплитуды напряжения(тока) к его действующему (эффективному) значению.
Коэффициент амплитуды (пикфактор сигнала) – это отношение ампплитуды напряжения(тока) к его действующему (эффективному) значению.
где T -период усреднения (Больше-лучше)
(нарисовать и пояснить почему)
Под коэффициентом формы (формфактором сигнала) принято считать отношение эффективного (действующего) значения напряжения (тока) к его средне-выпрямленному значению (среднему значению модуля).
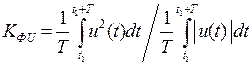



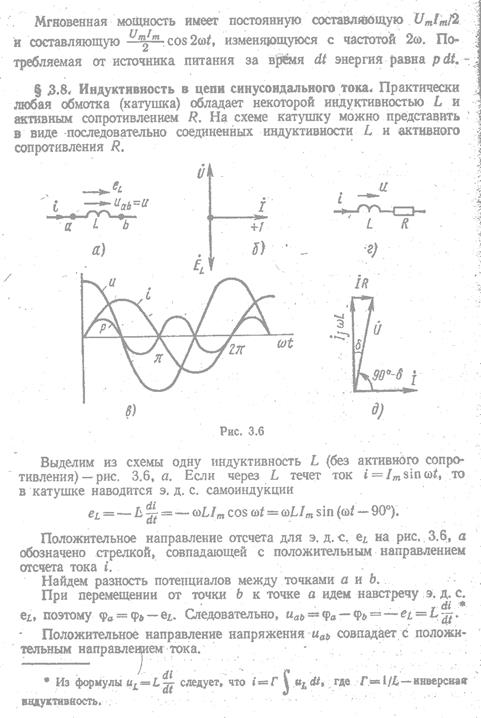
Активные и реактивные сопротивления










 | |||
 |
Векторные диаграммы неразветвлённой и разветвлённой цепей.



Явления резонанса в электрических цепях.



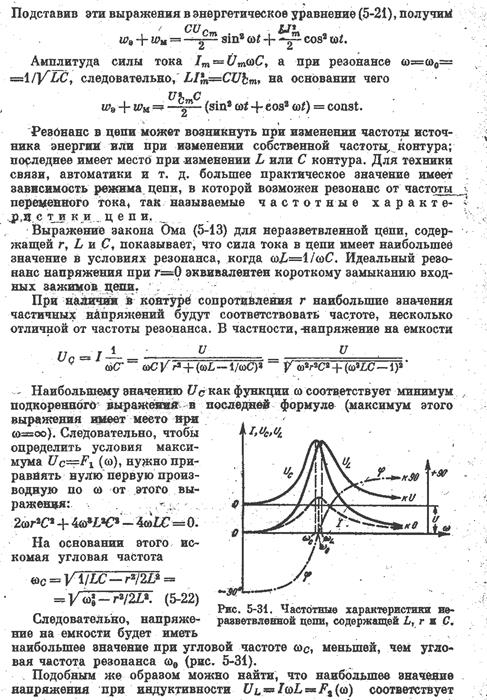





Дать примеры определения H – параметров для простейших цепей.
Дать h – параметры в дифференциальной форме
Частотные и фазовые характеристики четырёхполюсников. Передаточная функция.
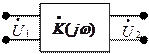
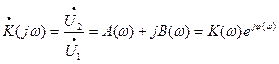 Четырёхполюсник может характеризоваться одним параметром, устанавливающим связь между выходным и входным напряжениями. При синусоидальном сигнале такой характеристикой является передаточная функция цепи (комплексный коэффициент передачи).
Четырёхполюсник может характеризоваться одним параметром, устанавливающим связь между выходным и входным напряжениями. При синусоидальном сигнале такой характеристикой является передаточная функция цепи (комплексный коэффициент передачи).
, где:
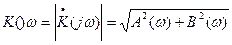 |
амплитудно-частотная характеристика
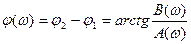 |
четырёхполюсника, а его фазо-частотная характеристика,
а 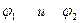 - начальные фазы, соответственно входного и выходного колебания.
- начальные фазы, соответственно входного и выходного колебания.
Таким образом, амплитудно-частотная характеристика показывает, во сколько раз амплитуда выходного колебания четырёхполюсника отличается от амплитуды входного гармонического колебания с частотой ω.
Фазо-частотная характеристика отображает сдвиг по фазе выходного колебания, по отношению к фазе входного.
Определим эти характеристики для простейших цепей.
 1. Интегрирующая (удлиняющая) цепочка.
1. Интегрирующая (удлиняющая) цепочка.
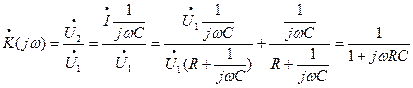
Избавимся от комплексности в знаменателе, чтобы представить правую часть в нормальной (алгебраической) форме домножив числитель и знаменатель на сопряжённое ему число.
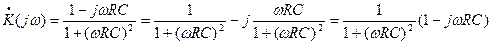
Определим модуль передаточной функции (амплитудно-частотную характеристику) цепочки,
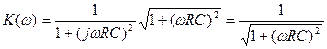

 и его фазо-частотную характеристику:
и его фазо-частотную характеристику: 
Пояснить ход кривых.
Теперь можем записать передаточную характеристику интегрирующей цепочки в комплексной форме.
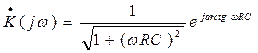
.
 2. Дифференцирующая (укорачивающая) цепочка.
2. Дифференцирующая (укорачивающая) цепочка.

Определим модуль передаточной функции (амплитудно-частотную характеристику) цепочки,
и её фазо-частотную характеристики.
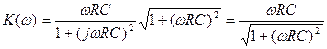 ,
, 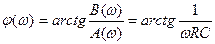 .
.


Пояснить ход кривых.
Передаточная функция дифференцирующей цепочки:
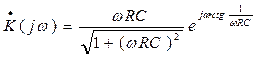
Передаточная функция линейной цепи вследствие принципа суперпозиции позволяет анализировать прохождение сложного сигнала через цепи (четырёхполюсники).
 С этой целью, учитывая, что передаточная функция есть комплексная функция мнимой частоты, входное колебание необходимо также представить в комплексной форме.
С этой целью, учитывая, что передаточная функция есть комплексная функция мнимой частоты, входное колебание необходимо также представить в комплексной форме.
 Разложение периодических колебаний произвольной формы в ряд Фурье.
Разложение периодических колебаний произвольной формы в ряд Фурье.

 Известно, что любую периодическую функцию - удовлетворяющую условиям Дирихле, с периодом и частотой повторения можно представить рядом Фурье:
Известно, что любую периодическую функцию - удовлетворяющую условиям Дирихле, с периодом и частотой повторения можно представить рядом Фурье:

-первая форма записи, где
 |  |

 для k=0 и для k>0.
для k=0 и для k>0.


 Где: постоянная составляющая периодического колебания, - амплитуда k –той гармоники, -начальная фаза k –той гармоники.
Где: постоянная составляющая периодического колебания, - амплитуда k –той гармоники, -начальная фаза k –той гармоники.
Разложив синус суммы углов, получим:

- вторая форма записи,

где:
 |  |  |
Здесь,,.
 |  |
При этом.
Особенности разложения в ряд Фурье периодических колебаний, обладающих симметрией по отношению к осям координат.
Здесь возможно 3 различных основных случая:

1. Колебание симметрично относительно оси абсцисс, т.е.


 При разложении таких кривых в ряд Фурье, будет отсутствовать постоянная составляющая и все гармоники с чётными номерами, т.е.
При разложении таких кривых в ряд Фурье, будет отсутствовать постоянная составляющая и все гармоники с чётными номерами, т.е.
 Поэтому ряд может быть записан так:
Поэтому ряд может быть записан так:
2. 
 Колебание симметрично относительно оси ординат, т.е.
Колебание симметрично относительно оси ординат, т.е.

 В таком колебании отсутствуют все синусные составляющие и присутствуют только постоянная и косинусные составляющие т.е. Следовательно ряд Фурье
В таком колебании отсутствуют все синусные составляющие и присутствуют только постоянная и косинусные составляющие т.е. Следовательно ряд Фурье
может быть записан так:

Пояснить по формулам коэффициентов! (Чётная функция).

3.  Колебание симметрично относительно начала координат, т.е.
Колебание симметрично относительно начала координат, т.е.
 Разложение имеет вид:
Разложение имеет вид:
 ,
,
т.е. здесь отсутствуют все косинусные и постоянная составляющие.
Пояснить по формулам коэффициентов! (Нечётная функция).
В общем случае, если функция не обладает симметрией по отношению к осям координат, то
разложение её в ряд Фурье содержит постоянную составляющую и все гармоники как чётные так и нечётные и все синусные и косинусные составляющие.
Ряд Фурье в комплексной Форме.

 Воспользовавшись формулой Эйлера, можно записать:
Воспользовавшись формулой Эйлера, можно записать:
.

Приняв обозначения: - комплексные амплитуды гармоник,
Можно записать ряд Фурье в комплексной форме:

Таким образом ряд Фурье в комплексной форме позволяет представить произвольную периодическую функцию времени как множество гармонических колебаний с комплексными амплитудами 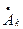 и дискретными частотами
и дискретными частотами 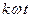 .
.
Умножив каждую комплексную амплитуду на передаточную функцию цепи(четырёхполюсника), получим множество комплексных амплитуд выходного колебания четырёхполюсника, с теми же
что и на входе частотами, т.к. при прохождении сигнала через линейные цепи новых частот(не содержащихся во входном колебаний) возникнуть не может.
Тогда выходное колебание четырехполюсника можно записать так:

Обозначим: 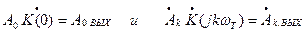 , тогда выходное колебание
, тогда выходное колебание

Суммируя члены ряда, можно получить выходное колебание, как функцию времени.
Интеграл Фурье.
Для определения выходного колебания четырёхполюсника на входе которого действует непериодическое колебание произвольной формы, процедура остаётся той же, те каждая спектральная составляющая входного сигнала умножается на передаточную функцию и затем производится суммирование всех выходных составляющих.
Однако, в этом случае, входное колебание представляется не дискретным рядом спектральных составляющих, а непрерывной функцией мнимой частоты 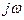 .
.
Любую непрерывную функцию можно представить как соответствующую периодическую, при  . Но, при этом, поскольку
. Но, при этом, поскольку 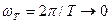 , интервалы между дискретными частотами спектральных составляющих и их амплитуды стремятся к нулю.
, интервалы между дискретными частотами спектральных составляющих и их амплитуды стремятся к нулю.
Функция 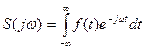 , полученная в результате такого предельного перехода, называется спектральной плотностью мощности колебания, или просто его спектром.
, полученная в результате такого предельного перехода, называется спектральной плотностью мощности колебания, или просто его спектром.
 Величина
Величина 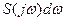 отображает суммарную мощность гармонических колебаний, заключённых в интервале частот
отображает суммарную мощность гармонических колебаний, заключённых в интервале частот 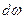 . Переход от функции времени к спектральной плотности мощности называется прямым преобразованием Фурье.
. Переход от функции времени к спектральной плотности мощности называется прямым преобразованием Фурье.
Обратное представление функции времени через спектральную плотность мощности
 называют обратным преобразованием Фурье.
называют обратным преобразованием Фурье.
Теперь определение выходного колебания линейного четырёхполюсника сводится к следующей процедуре:

Здесь 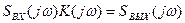 - спектральная плотность мощности выходного колебания четырёхполюсника.
- спектральная плотность мощности выходного колебания четырёхполюсника.
Таким образом, зная реакцию линейного четырёхполюсника на гармоническое воздействие, т.е. зная его передаточную функцию 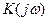 , можно определить выходное колебание при любой форме входного колебания. При этом гармоническое колебание можно рассматривать как некоторый испытательный (тестовый) сигнал, позволяющий исследовать четырёхполюсник в частотной области представления сигналов и свойств линейных цепей.
, можно определить выходное колебание при любой форме входного колебания. При этом гармоническое колебание можно рассматривать как некоторый испытательный (тестовый) сигнал, позволяющий исследовать четырёхполюсник в частотной области представления сигналов и свойств линейных цепей.
Импульсная и переходная характеристики четырёхполюсника.
Для исследования свойств четырёхполюсников, наряду с гармоническим колебанием широко используются и другие колебания. Наиболее распространёнными из них являются единичный перепад 1(t) (ступенька) и δ -функция.


Очевидно, что 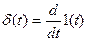 и обратно
и обратно 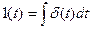 .
.
Реакция четырёхполюсника на единичный перепад 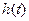 называется переходной характеристикой цепи (четырёхполюсника), его реакция на дельта-функцию g(t) – импульсной характеристикой.
называется переходной характеристикой цепи (четырёхполюсника), его реакция на дельта-функцию g(t) – импульсной характеристикой.
Обе эти характеристики описывают четырёхполюсник во временной области представления сигналов и свойств линейных цепей и могут быть получены в результате решения дифференциальных уравнений цепей.
Однако при известной передаточной функции четырёхполюсника они могут быть определены следующим образом:
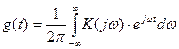 ,
,  . При этом
. При этом 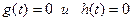 при t<0, т.к. отклик на выходе не может появиться раньше воздействия на вход соответственно
при t<0, т.к. отклик на выходе не может появиться раньше воздействия на вход соответственно 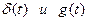 .
.
Эти условия приводят к ограничениям, которые накладываются на функцию 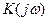 , которая должна удовлетворять критерию Пэли-Винера:
, которая должна удовлетворять критерию Пэли-Винера: 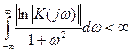 .
.
Кроме того, учитывая, что 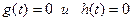 суть вещественные функции времени,
суть вещественные функции времени, 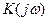 должна также удовлетворять следующему условию:
должна также удовлетворять следующему условию: 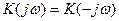 , т.е. модуль передаточной функции (АЧХ) должен быть чётной, а аргумент (ФЧХ) нечётной функцией частоты. Большинство функций
, т.е. модуль передаточной функции (АЧХ) должен быть чётной, а аргумент (ФЧХ) нечётной функцией частоты. Большинство функций 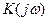 , описывающих реальные четырёхполюсники (цепи), этим условиям удовлетворяют. Принимая во внимание, что
, описывающих реальные четырёхполюсники (цепи), этим условиям удовлетворяют. Принимая во внимание, что 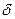 -функция является идеализацией, на практике импульсную характеристику можно получить подавая на вход четырёхполюсника короткий импульс достаточно большой амплитуды и укорачивая его длительность до тех пор пока отклик на выходе не перестанет изменяться по форме.
-функция является идеализацией, на практике импульсную характеристику можно получить подавая на вход четырёхполюсника короткий импульс достаточно большой амплитуды и укорачивая его длительность до тех пор пока отклик на выходе не перестанет изменяться по форме.
Существует и обратное соотношение: 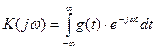
Для понимания физического смысла приведённых преобразований определим спектр дельта-функции.
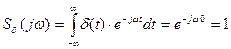 , т.е. спектр дельта функции представляет собой колебания с единичными амплитудами и нулевыми начальными фазами, поэтому спектральная плотность выходного колебания четырёхполюсника, совпадает с его передаточной функцией, и его импульсная реакция образуется в результате суммирования (интегрирования) всех составляющих спектра выходного сигнала, амплитуды которых равны значениям амплитудно-частотной характеристики, а фазы значениям фазо-частотной характеристики четырёхполюсника.
, т.е. спектр дельта функции представляет собой колебания с единичными амплитудами и нулевыми начальными фазами, поэтому спектральная плотность выходного колебания четырёхполюсника, совпадает с его передаточной функцией, и его импульсная реакция образуется в результате суммирования (интегрирования) всех составляющих спектра выходного сигнала, амплитуды которых равны значениям амплитудно-частотной характеристики, а фазы значениям фазо-частотной характеристики четырёхполюсника.
 Преобразование Лапласа.
Преобразование Лапласа.








Закон Ома в операторной форме. 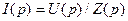
Первый закон Кирхгофа в операторной форме. 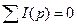
Второй закон Кирхгофа в операторной форме. 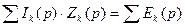
 Обратное преобразование Лапласа.
Обратное преобразование Лапласа.





|
|
|
|
Дата добавления: 2015-05-06; Просмотров: 1715; Нарушение авторских прав?; Мы поможем в написании вашей работы!