Электрическими установками

ДИСКРЕТНОГО ЛОГИЧЕСКОГО УПРАВЛЕНИЯ

ИЗУЧЕНИЕ СПОСОБОВ ПОСТРОЕНИЯ УСТРОЙСТВ

Лабораторная работа №9

Цели работы: 1. Изучение основ описания структурных схем дискретного логического управления электроприводами и другими объектами дискретного управления.

2. Ознакомление со способами составления матема­ти­ческой формулы структуры логической схемы управ­ления по графически изображённой структуре системы и по решению обратной задачи.

Оборудование: 1. Лабораторный стенд.

2. Соединительные провода.

Рекомендательный библиографический список: [1], Гл.7: §§7.6.2 – 7.7; [5], Гл.22: §22.7; [6]: §4; [9], Гл.14: §§14.1 – 14.6; [10], Гл.15: §§15.1 – 15.3.

Среди многообразия систем автоматического управления электро­при­водами и другими объектами автоматизации важное место при практическом применении занимают сис­темы, формирующие управляющее воз­действие на объект путем логического анализа ограниченного числа дискретных состояний отдельных частей, параметров объекта и самой системы. В первую очередь к ним относятся различные релейные схемы управления, выполняемые на контактных или бесконтактных элементах. Контактными элементами являются реле, контакторы, кнопки управления, конечные и путевые выключатели, автоматы, имеющие электрические контакты, размыкающие и замыкающие электрические цепи. Бесконтакт­ные элементы представляют собой магнитные, полупроводниковые либо другие электронные и пневматические устройства, работающие в ключевых режимах. Все эти элементы на выходе дают только два уровня сигнала: высокий или низкий, т.е. обеспечивают релейное действие.

Схема управления в общем случае обрабатывает исходную информацию о событиях (промежуточные или крайние положения определенных органов стан­­ка, машины, агрегата; предельные превышения над установкой определенных величин и т.п.), заданных в виде дискретных сигналов, типа «включено-выключено». Если указанные состояния (события a, b, c, d и т.д.) отображаются в виде дискретных сигналов, например, высокого и низкого уровней, то данное резкое различие и сам факт существования события можно формально представить с помощью математического ап­парата алгебры логики. В этой алгебре только две переменные величины: логические 0 и 1. Сами величины 0 и 1 особого значения не имеют, а ис­пользуются только для обозначения того факта, что некоторое событие (например, замыкание контакта реле) произошло. Если появление события (замыкание контакта, наличие высокого уровня сигнала) обозначить логической 1, то отсутствие этого события (размыкание контакта, появле­ние низкого уровня сигнала) формально можно отобразить логическим 0.

Рассмотрим простейшую схему, состоящую из одной кнопки с самовозвратом SB и реле К (рис. 9.1а).

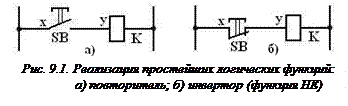Из схемы следует, что при нажатии кнопки SB ее контакт замкнётся и реле К сработает. Обозначив через y реле и считая y в дальнейшем за­висимой логической функцией, а через x кнопку – независимую переменную, можно схему на рис. 9.1а математически описать как: y = x. С учётом двух возможных значений логических переменных ясно, что данное выражение в смысле логической взаимосвязи выходного и входного сигналов описывает функцию повторителя.

На рис. 9.1б представлена простейшая схема, на которой реле К вклю­чено последовательно с размыкающим контактом кнопки SB. Ясно, что реле отключится, если кнопку нажать, и сработает, если кнопку отпус­тить. Поведение схемы можно описать выражением: 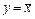. Черта над переменной х означает, что состояние элемента у (события) противопо­ложно (инверсно) состоянию (событию) элемента х. Такую логическую функцию называют инверсией или функцией НЕ (логическое отрицание), а схему – инвертором.

Вводя в рассмотрение две независимые логические переменные х ₁ и х ₂, определяющие зависимую логическую функцию у в соответствии со схе­мами управления реле от кнопок на рис. 9.2а и 9.2б, можно для первой схемы получить математическое описание в виде: у = х ₁∙ х ₂, что соот­ветствует операции логического умножения (конъюнкции), а для второй – в виде: у = х ₁ + х ₂, что соответствует операции логического сложения (дизъюнкции).

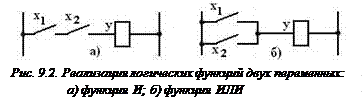На рис. 9.2 реле управляются замыкающимися контактами х ₁ и х ₂.

Если реле будут управляться размыкающимися контактами, то контакты должны быть обозначены теми же буквами, но с чертой сверху (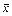). Это будет означать, что контакты являются инверсными.

Представленные схемы и их математические описания представляют собой простейшие логические операции, позволяющие реализовать в комбинации сложные логические функции и соответствующие им схемы.

Логическую взаимосвязь между событиями (сигналами) в электричес­ких схемах можно пояснить следующим образом:

· Схемой повторителя называют схему, реализующую логическую операцию повторе­ния, сигнал (событие) на выходе которой в логи­ческом смысле всегда эквивалентен входному сигналу.

· Схемой НЕ называют схему, реализующую операцию ло­гического отрицания, значение сигнала на выходе которой всегда проти­вопо­ложно (инверсно) логическому значению входного сигнала.

· Схемой И называют схему, реализующую операцию логичес­кого умножения, сигнал (событие) на выходе которой имеет место при возникновении обоих сигналов на её входах.

· Схемой ИЛИ называют схему, реализующую операцию логи­ческого сложения, сигнал (событие) на выходе которой имеет место при возникновении сигнала хотя бы на одном из её входов.

Для составления структурных схем логического управления электро­приводами и объектами автоматизации используют условные графичес­кие изображения логических элементов (схемная реализация которых разнообразна), логическую взаимосвязь между независимыми и зависимыми переменными в виде таблиц истинности, временные диаграммы сиг­налов, поясняющих действие логических схем. Подробнее об этом см. в [6].

Схему, реализующую логическую зависимость между зависимой и независимой переменными (событиями, сигналами), принято называть струк­турной логической (релейной) схемой, которая в свою очередь может быть описана структурной математической формулой.

Структурная схема – это изображение, показывающее количество и состав реагирующих на событие a, b, c, d, и т.д. органов или структурных элементов и соединения между ними.

На рис. 9.3 в качестве примера приведён узел контактной релейной схемы и его структурная схема. На рис. 9.3а изображены контакты релейных элементов, которые реагируют на события a, b, c и т.д. Одни из них замкнуты, другие – разомкнуты. На структурной схеме (рис. 9.3б) замыкающие контакты обозначены буквами без черточек сверху, размыкающие – с черточками.

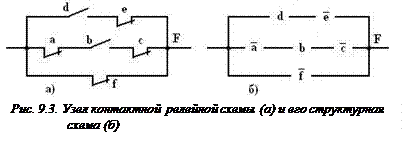При описании схемы структурной математической формулой обозначают последовательное соединение элементов знаком логического умножения, а параллельное – знаком логического суммирования и записывают обозначения всех структурных элементов, проходя по всем последовательным и параллельным цепям схемы. Структурная формула для изображенного узла имеет вид:

.

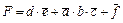Читать данную формулу можно следующим образом: событие F имеет место (логическая функция F(a, b, c,...) единична) при возникновении события d и отсутствии события е или при возникновении события b и отсутствии событий a и с, или при отсутствии события f.

Логическая функция может быть записана аналитически (и реализована технически) различными сочетаниями операций сложения и умножения переменных. Однако с точки зрения представления логической функ­ции и последующего синтеза логической схемы используют наиболее удобные формы записи:

· В виде суммы произведений логических переменных.

· В виде произведения сумм.

Это соответствует дизъюнктивной (ДНФ) и конъюнктивной (КНФ) нормальным формам представления логических функции. Дальнейший шаг – переход к совершенным дизъюнктивной (СДНФ) и конъюнктивной (СКНФ) нормальным формам. Подробнее об этом см., например, в [10].

Дата добавления: 2015-05-06