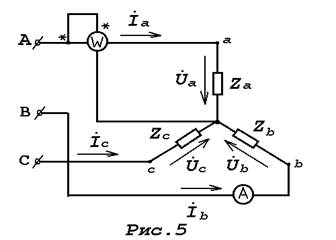
Где UA, UB,UC – комплексные напряжения источника питания. 1 страница

Yַ_a = 1/Z_a ; Y_b = 1/Z_b; Y_c= 1/Z_c; Y_N = 1/Z_N – комплексные проводимости фаз и нейтрального провода.

Комплексный ток в нейтральном проводе находят в соответствии с уравнением, составленным по первому закону Кирхгофа для нейтральнoй точки n цепи:

I_n۠=I_a+I_b+I_c.

Комплексные фазные напряжения приёмника электроэнергии находят из уравнений; составленных по второму закону Кирхгофа для замкнутого контура:

U_a=U_A- U_nN; U_b=U_B- U_nN; U_c=U_C- U_nN.

При этом фазные токи приёмника определяют по закону Ома для соответствующих участков цепи:

I_a=U_a/Z_a; I_b=U_b/Z_b; I_c=U_c/Z_c.

Трёхфазная система обеспечивает приёмники электроэнергии симметричным питанием. При этом активная, реактивная и полная мощности могут быть определены по следующим формулам с учётом знака реактивных сопротивлений:

P = I_А²R_а + I_В²R_b + I_С²R_c =U_aI_A cosφ_а + U_b I_B cosφ_b +U_cI_C cosφ_с;

Q= I_А²X_a + I_В²X_b + I_С²X_c =U_a I_A sinφ_а + U_b I_b sinφ_b + U_c I_С sinφ_с;

S = √P²+Q² = I_А²Z_a + I_В²Z_b + I_С²Z_c;

где cosφ_а= R_a/ Z_a; cos φ_b = R_b/ Z_b; cos φ_с= R_c/ Z_c

sin φ_а= X_a/ Z_a; sin φ_b = X_b/ Z_b; sin φ_с = X_c/ Z_c.

При симметричной нагрузке эти формулы приводят к виду:

P= 3 I_ф²R_ф= √3U_Л I_Л cos φ_ф;

Q= 3 I_a²Xa= √3U_K I_K sin φ_a$

S= √P²+Q² = √3U_Л I_Л,

где cos φ_ф = R_ф/ Z_ф; sin φ_ф = X_ф/ Z_ф.

6.3 Несимметричные режимы в трёхфазной электрической цепи при соединении приёмников электроэнергии “звездой”

При обрыве линии (или фазы приёмника электроэнергии) в трёхпроводной системе Y-проводимость соответствующей фазы приёмника, например фазы С равна нулю, т.к. сопротивление равно ∞. Следовательно, несколько изменится напряжение между нейтральными точками системы UnN:

U_nN= 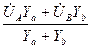, где Yc=0

Фазные напряжения приёмника определяют как:

U_a=U_А- U_nN; U_b=U_В- U_nN; U_c=U_С- U_nN.

Фазные токи приёмника по закону Ома:

I_a=U_a/Z_a; I_b=U_b/Z_b; I_c=0.

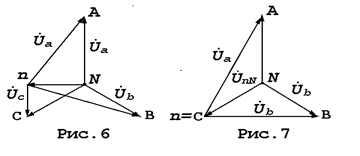
Векторная диаграмма напряжений при обрыве фазы (холостой ход) приёмника изображена на рис.6.

При коротком замыкании фазы С приёмника электроэнергии в трехпроводной системе потенциалы нейтральной точки n и начала фазы с приёмника будут равны, т.е. φ_n = φ_c.

Векторная диаграмма напряжений при коротком замыкании фазы с приёмника электроэнергии представлена на рис.7.

Напряжение смещения U_nN= U_C, а фазные напряжения приёмника определяются как:

U_a=U_A- U_nN= U_A- U_C; U_b=U_B- U_nN= U_B- U_C; U_c=0.

Фазные токи приёмника по закону Ома:

I_a=U_a/Z_a; I_b=U_b/Z_b:

Ток короткого замыкания по первому закону Кирхгофа для нейтральной точки n

۠I_кз= I_а + I_b.

Таблица 3

№ вар.	Zа, Ом	Zb, Ом	Zc, Ом	UЛ,В	К.З. фазы	Обрыв линии
	15+j10	10-j20	J40		a
	10-j10	20+j20	10e^j30			A
	15-j20		20e^j45		в
	20+j10	J30				В
	30۟	10е^j45	10-j20		c
	4e^j40	-j20	15+j10			C
	20e^-j30	j15	10+j10			A
	10e^j90	10+j15			a
	j40	15e^-j45	40-j10		в
	-j20	10e^j30				B
	10-j10	20+j10	15e^j45		c
	20+j20		30e-j90			C
	10e^-j90	10+j20			a
	15e^j60		-j30			A
	25e^j45	10+j30	10e^j90			B
	10+j10	20-j10			в
	20-j20	10+j10	20e^-j30			B
	5-j10	10+j5	10e^j45		a
	25+j25	10-j20	30e^j30			A
	20ej30	10+j20	30e-j40		c
		40-j20	20+j40			A
	10+j30	20e-j90			a
		10-j20	30+j10			В
	30-j10		20+j20		в
	40-j20	30ej45				C
		20ej30	30e-j60		c
		20+j10	30-j30			A

		10+j30	30e^-j90		a
	20-j20		50e^j90			B
	50e^j90		40-j10		c
	40-j40		30e^j45			C
	10-j10	20e^30			в
		25e^j45	30e^-j30			A
	20+j10		20e^-j45		a
		30e^-j60	25e^j30			B
		10-j8	20+j10		в
	10	20+j10	10-j30			A
	40e^j45		10-j30		c
	10e^-j90		10+j20			C
		20+j20	30-j10		a
		30-j20	20+j40			A
		20-j30	40+j10		b
	10+j5	10-j10				B
		20e^j90	10-j20		c
		30-j40	20+j30			A
	20-j30		30+j20			C
	20e^j30	40-j45			a
	20e^j60	30-j30				B
	30+j10	40-j20			c
	15-j20	20+j20				A
	25e^j30	15-j60			в
	20-j40		30e^j45			C
		25-j25	10+j15		c
	10e^j45	15-j10				A
	10e^-j30	10+j10				B
	10-j5	15+j5			a

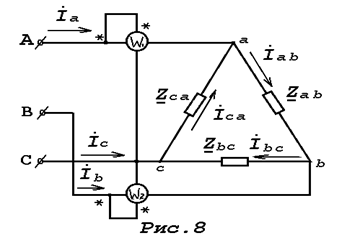
Задача 4. Анализ трёхфазной электрической цепи при схеме соединения приёмников “треугольником”.

Потребитель электроэнергии, фазы которого имеют комплексные сопротивления: Z_ab, Z_bc, Z_ca и соединены в трёхфазную электрическую цепь “треугольником” (рис.8), питается симметричной системой линейных напряжений: U_AB= U_BC= U_CA= U_л.

С учётом данных, приведённых в таблице 4. Для каждого варианта задания, определить:

1. фазные и линейные токи потребителя;

2. активную Р, реактивную Q и полную S мощности потребителя;

3. показания ваттметров W₁,W₂;

4. построить векторную диаграмму токов и напряжений;

7) Краткие теоретические положения.

7.1 Трёхфазные электрические цепи при соединении фаз приёмника “треугольником”.

В связанных трёхфазных системах наряду с соединением трёхфазных потребителей “звездой” применяется соединение фаз “треугольником”. При этом не имеет значения как соединены фазы источника - “звездой ” или “треугольником”.

При соединении “треугольником” фазные напряжения оказываются равными линейным напряжением: U_Л=U_Ф

U_АВ= U_ав; U_BC =U_вс; U_СA=U_са.

Соотношение между линейными и фазными токами определяют из уравнений, составленных для токов в соответствии с первым законом Кирхгофа для узлов a,b,c разветвления электрической цепи:

I_А=I_ав- I_са; I_В=I_вс- I_ав; I_С=I_са- I_вс.

При симметричной нагрузке линейные токи I_A= I_B= I_C= I_Л и фазные токи I_aв= I_вс= I_са= I_ф. При этом угол сдвига фаз между фазными токами и напряжениями φ_ab= φ_bc= φ_ca= φ_ф.

В соответствии с этим при симметричной нагрузке имеет место соотношение: I_Л=√3 I_ф.

При обрыве любой линии питания приёмник оказывается включён на соответствующее линейное напряжение источника, причём две фазы приёмника будут включены последовательно. В таком случае необходимо воспользоваться схемой замещения. Это будет однофазная цепь, имеющая направления токов и напряжений согласно исходной трёхфазной системе.

Таблица 4.

№ вар	Zав, Ом	Zвс, Ом	Zса, Ом	UЛ, В	Обр. в линии	Обрыв фазы
	7+j7	10+j10	4-j4		А
	10-j10	10e^j^90	-j20		В
	20+j10	15e^j^45	-j40			са
	20-j15	10e^-^j^90			С
	30+j20		-j40		А
	8+j8	12e^-j60	15-j5			вс
	10+j30	15e^-j30	20+j10		А
	30-j20	20e^j90	15+j5		В
		15+j15	15-j10		С
	20e^j90	25+j20	15+j15			са
	15e^-j45	20+j20	10-j10		А
	15e^j45	-j30			В
	15-j10	10+j20	5-j10			вс
		10e^j30	10-j10		А
	15e^j30	20-j10	-j20		С
	8-j8	10+j10				ав
	10e^j45		10-j20		A
		40-j10	20+j20		B
	50e^j90		30-j30			ab
	10-j8	20+j10			A
	20e^-j30	20+j10			B
		50-j10	30+j30		C
		10-j10	15e^j60		A
	20-j10		20e^j30		A
	10-j50		50e^j90		C
	20e^-j45		10e^j90			bc
		10-j5	15e^j90		B
		10-j50	25+j25			ca
		10-j20	20e^j30		A
		10-j10	20e^j45		B
	60e^j90	50-j20			C
	30e^j30	30-j30			A
		20+j10	20-j30		B
		50-j10	40+j20		C
		40+j20	20-j10		A
		10-j20	20+j10		A
		20-j10	20e^j60		B
		40+j40	30-j50			ab
	20e^j90	20-j10	30-j5		C
	20e^-j90	10+j10			B
	60e^j90	50-j10			A
	20e^j45	25-j25			C
	10-j15		20+j30		B
		10-j20	20+j5		A
	15e^j30	20e^-j60			C
		50-j10	10+j50			bc
		50e^j90	40-j20		C
	20e^j45	30-j20			B
	30e^-j30	20+j20			A
	30+j20	25-j10			C
	10-j20	25+j25	15e^j^90			ca
	20e^j45	30-j10			B
	10+j20		15-j10		A
	10-j25	15e^j30			C
	10-j10	20e^j30			A
	10e^j30		25e^-j10		C

Задача 5. Анализ работы однофазного трансформатора

Однофазный трансформатор имеет напряжение U₁/U₂ B. Номинальная мощность трансформатора S,кВА. Опыт xолостого xода проведён при номинальном напряжении в первичной обмотке. Данные опытов холостого хода и короткого замыкания:

P_ХХ; I_ХХ; P_КЗ; U_К%; частота f=50Гц. P_ХХ=3,6%Sном; P_КЗ=4,8%Sном.

Магнитопровод трансформатора изготовлен из пластин толщиной 0,5мм; удельные потери р10 [Вт/(кг. Тл²)]

Определить:

а) массу магнитопровода mст., если максимальное значение индукции в стержне и в ярме Вмах [Тл];

б) действительное поперечное сечение стержня Аст., если коэффициент заполнения пакета сталью к_З и w2;

в) сопротивления магнитопровода трансформатора полное, активное и реактивное и угол магнитного запаздывания α;

г) параметры обмоток трансформатора R₁,R₂,X₁,X₂. При расчёте принять, что в опыте короткого замыкания мощность потерь делится поровну между первичной и вторичной обмотками.

д) кпд трансформатора при активно-индуктивной нагрузке при cosφ₂ и значениях коэффициента загрузки: 0,1; 0,25; 0,5; 0,75; 1,0.

8) Краткие теоретические положения.

8.1 Однофазный трансформатор.

Трансформатором называют статическое электромагнитное устройство с двумя или большим числом индуктивно связанных обмоток, предназначенное для преобразования переменного тока одного напряжения в переменный ток другого напряжения. В трансформаторе передача энергии из сети к приёмнику происходит посредством переменного потока.

При синусоидальном изменении напряжения источника питания U₁ с частотой f поток магнитопровода Ф оказывается практически синусоидальным. ЭДС самоиндукции и взаимоиндукции:

E₁=4,44 W₁ f Ф_m,

E₂=4,44 W₂ f Ф_m.

Коэффициент трансформации трансформатора может быть определён как:

К = E₁/E₂ = L₁/L₂ = W₁/W₂= U₁/U₂ ≈ I₂/I₁.

Для определения величин, характеризующих работу трансформатора под нагрузкой, проводятся два опыта: опыт холостого хода и опыт короткого замыкания.

Опыт холостого хода. Вторичная обмотка разомкнута, к первичной подаётся номинальное напряжение. Определяются следующие величины:

I_ХХ; P_ХХ=P_СТ.; K; U_2ХХ.

По опытным данным холостого хода можно вычислить параметры сердечника магнитопровода:

Rm = P_ХХ/I_ХХ²; Zm = U_ХХ/I_ХХ; X_m= √Z_m²-R_m²;

Коэффициент мощности холостого хода: cos φ _XX =R_m/Z_m,

Угол магнитного запаздывания: α = 90˚- φ _ХХ.

Опыт короткого замыкания проводится при пониженном напряжении на первичной обмотке в отличие от аварийного короткого замыкания. Напряжение подводится такое, при котором токи в обмотках достигают номинальных значений.

Определяется: Р_КЗ, U_КЗ=(U_КЗ% 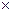U_Н /100%).

Опытные данные позволяют определить сопротивления короткого замыкания.:

R_К = P_КЗ/I_1Н²; Z_К = U_КЗ/I_1Н; X_К= √Z_К²-R_К².

Для силовых трансформаторов можно принять, что мощность потерь короткого замыкания делится поровну между первичной и вторичной обмотками. Это позволяет определить параметры обмоток трансформатора:

R_К = R₁ +R₂΄ = R₁ +R_2К²; R₁≈ R_2К²

X_К = X₁ +X₂΄ = X₁+X_2К²; X₁ ≈ X_2К²

Z_К = Z₁ +Z₂΄ = Z₁ +Z_2К².

Мощность короткого замыкания даёт возможность определить потери в обмотках: Р_М=β²P_КЗ, где коэффициент загрузки трансформатора

β = I₂/I_2Н.

Коэффициент полезного действия трансформатора

η = P₂/P₁= P₂/(P₂+P_М+Р_КЗ)=S_Н 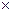β 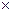cos φ₂ / (S_Н 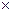β 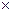cos φ₂+ β² 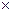P_КЗ+ +P_СТ)

кпд имеет максимальное значение при загрузке

β = √Р_СТ/P_КЗ

Массу магнитопровода можно рассчитать, если известны полные и удельные потери в стали.

Удельные потери при заданной индукции

р = р₁₀ 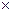В_m²; полные потери в стали Р_СТ=Р_ХХ, тогда масса магнитопровода m_СТ =Р_СТ/Р:

Дата добавления: 2015-05-06