Вектор состояния

Согласно аксиоматике квантовой механики, состояние – это полное описание замкнутой системы в выбранном базисе, которое формализуется лучом в гильбертовом пространстве (вектором состояния).

Что такое гильбертово пространство, понять довольно просто – это пространство состояний системы, некоторое множество ее возможных состояний. Оно задается набором собственных (базисных, основных) состояний системы, которые нас интересуют в каком-то конкретном случае.

При этом в зависимости от поставленной задачи мы можем выбирать тот или иной набор базисных состояний и записывать различные векторы состояния для одной и той же системы. Например, нас может интересовать, как изменяются пространственные координаты частицы, и тогда выбирается бесконечномерное гильбертово пространство, поскольку координата – непрерывная величина, и с каждой точкой сопоставимо отдельное состояние частицы. Но нас может интересовать иная задача – как у той же частицы ведет себя спин. Тогда можно будет записать уже другой вектор состояния, выбирая в качестве базиса, скажем, два состояния спина, которые возможны для нашей частицы: спин-вверх и спин-вниз. И в том, и в другом случае это будут полные описания, поскольку охватываются все возможные координаты или ситуации со спином. Полнота описания в квантовой теории заключается не в том, что одновременно описывается все, что только возможно для данной системы. Речь о том, что мы имеем полное описание в рамках определенного набора состояний, которые нас интересуют.

Записывая вектор состояния системы в различных базисах, мы как бы анализируем систему с различных сторон, рассматриваем разные стороны ее проявления. При этом можно выбирать самые различные наборы состояний, записывая векторы состояний в любом базисе. Другой вопрос, нужно ли это делать? Что толку, если мы выберем набор базисных состояний, но система, которую нам хочется описать, эти состояния не принимает? Тогда вектор состояния, записанный для нашей системы, не будет иметь под собой никакой объективной основы – он не будет описывать выбранный нами элемент реальности. Другое дело, что не так-то просто бывает сказать, какие состояния существуют у данной системы. Например, нелегко догадаться, что у частиц могут быть спиновые степени свободы.

В этом плане интересна ситуация с системами, обладающими сознанием. Казалось бы, и так всем понятно, что работа сознания связана с различными состояниями. И этот момент у всех на виду – это не спины у частиц, поди еще, догадайся о них, да научись эти спины мерить. Что же мешает количественно описывать сознание методами квантовой теории? Если у человека есть вполне определенные состояния, связанные с работой сознания, и довольно легко можно выбрать состояния базисные – тогда есть все необходимое для того, чтобы использовать математический формализм квантовой теории. Скажем, для описания ментальной сферы деятельности сознания в качестве базисных состояний тогда вполне подойдет ограниченный набор слов – ведь мы постоянно произносим вслух или про себя какие-то слова. И их чередование – это смена нашего состояния. Таким образом, работу сознания можно описывать в терминах вектора состояния. И такое описание будет вполне естественным, будет иметь под собой реальную основу – объективные состояния системы. Это будет описание не каких-то чужеродных, не свойственных разумной системе состояний, а наоборот, самой важной ее характеристики – сознательной деятельности.

Что может дать такое описание? На мой взгляд – очень многое. Например, здесь открывается путь к количественному описанию, то есть к научной методологии и практической технологии «магии сознания». Скажем, ОВД (остановка внутреннего диалога) – прямой аналог нелокального суперпозиционного состояния, когда у нас нет никакого конкретного состояния сознания (определенного слова, чувства и т. д.), но мы можем «проявить» одно из них в «локальной» форме. А как говорил дон Хуан в книгах К. Кастанеды, ОВД – это ключ к магии. Здесь явная аналогия с квантовой теорией, где нелокальные суперпозиционные состояния – ключ ко всем «сверхъестественным» физическим проявлениям типа телепортации-телепатии.

Мы еще будем периодически возвращаться к этим вопросам, но пока я продолжу разговор об основных понятиях квантовой теории, связанных с вектором состояния.

Как уже говорилось, в квантовой теории принято различать чистые и смешанные состояния. Приведем определения.

Чистым состоянием (ЧС) называется такое состояние системы, которое может быть описано одним вектором состояния.

Смешанным состоянием называется такое состояние системы, которое не может быть описано одним вектором состояния, а может быть представлено только матрицей плотности.

Ключевой момент в понимании ЧС состоит в том, что система в принципе, пусть даже практически это сделать нереально, но может быть описана одной волновой функцией (вектором состояния, волновым вектором). И основное различие между чистым и смешанным состоянием в этом и заключается – существует или нет принципиальная возможность полностью описать состояние системы одним вектором состояния. Если это можно сделать – состояние чистое, если нет – смешанное.

Очевидно, что мы можем описать систему одним вектором состояния только в том случае, если она замкнута*, изолирована. Замкнутость – необходимое условие для ЧС. В противном случае система будет взаимодействовать с окружением и не может быть полностью описана одним лишь вектором состояния – придется учитывать волновые векторы окружения. Замкнутость – это также и достаточное условие для ЧС, поскольку вся информация, необходимая для полного описания системы, находится в ней самой, и ее достаточно для принципиальной возможности записать вектор состояния всей системы.

* Под замкнутостью понимается отсутствие любых корреляций системы с окружением, как классических, так и нелокальных квантовых.

В квантовой механике понятие чистого состояния и понятие замкнутой системы тождественны. Если квантовая система может быть описана одним вектором состояния, говорят, что она находится в чистом состоянии. Для замкнутых систем такая ситуация имеет место по определению.

Остановимся чуть более подробно на замкнутой системе и зададимся вопросом: «В каком состоянии должны находиться подсистемы, и какие корреляции между ними возможны, чтобы состояние всей системы оставалось замкнутым, то есть ЧС?»

Здесь возможны два варианта. Самый простой – когда вся система состоит из подсистем, каждая из которых, в свою очередь, сама является замкнутой. В данном случае каждая подсистема находится в ЧС, обладая при этом своим независимым вектором состояния в пространстве с размерностью меньшей, чем размерность всей системы (речь идет о гильбертовом пространстве). При таком условии вся система может быть разложена по независимым подсистемам. Вектор состояния всей системы (и размерность ее гильбертова пространства) будет равен тензорному* произведению векторов состояния подсистем. Такое состояние системы называется сепарабельным (разделимым).

* В отличие от обычного произведения матриц (строка на столбец), при тензорном умножении каждый элемент первой матрицы умножается на всю вторую матрицу. Это же относится к векторам как частному случаю матриц.

Это то, на чем стоит вся классическая физика. Если бы не существовало такого варианта чистого состояния, то не было бы и классической физики. Другой вариант ЧС – когда система находится в когерентной суперпозиции состояний всех ее подсистем.

Обычно именно этот вариант вызывает наибольшие трудности в понимании. Вероятно, потому, что мы не можем непосредственно увидеть и «пощупать» это состояние в окружающем мире, хотя на протяжении всей человеческой истории о нем говорится постоянно. Так что некоторые представления об этом состоянии замкнутой системы мы все же имеем. Например, для Вселенной, как замкнутой системы, – это Единый Источник классической реальности, Бог, Абсолют и т. п.

В терминах квантовой физики этот случай соответствует ЧС системы, в которой существуют лишь нелокальные квантовые корреляции. Такое состояние в квантовой физике называется чистым запутанным состоянием (ЧЗС).

И самое интересное, что классических корреляций в ЧС нет и быть не может.

Таким образом, ЧС бывают либо сепарабельными, либо ЧЗС. Третьего, как говорится, не дано.

И это не мои домыслы и предположения. Это строгий результат, следующий из основ квантовой теории. Например, об этом достаточно четко сказано в работе «Запутанные квантовые состояния атомных систем»*. В разделе 2.2 читаем: «Итак, чистые квантовые состояния бывают либо квантово-коррелированными (запутанными), либо вообще некоррелированными». Далее, в разделе 2.4 еще раз: «Как уже отмечалось, в случае чистых состояний любые корреляции являются квантовыми, то есть соответствуют запутанным состояниям».

* Баргатин И. В., Гришанин Б. А., Задков В. Н. Запутанные квантовые состояния атомных систем. УФН 171 (6), 625 (2001).

Напомню, что некоррелированность, то есть отсутствие вообще каких-либо корреляций, как классических, так и квантовых, – это сепарабельные состояния.

Итак, непосредственно из основ квантовой физики следует, что:

● замкнутая система находится в чистом состоянии;

● в замкнутой системе корреляции (и классические, и квантовые) между подсистемами могут отсутствовать вовсе (в случае не взаимодействующих подсистем, то есть сепарабельного состояния);

● в замкнутой системе корреляции между подсистемами могут быть только нелокальными квантовыми (для взаимодействующих подсистем);

● в замкнутой системе отсутствуют классические корреляции между ее подсистемами.

Напомню, что речь идет о произвольных замкнутых системах. И в полной мере эти выводы справедливы только для всего Универсума, как единственной системы, которая является по-настоящему замкнутой.

Здесь у многих сразу же может возникнуть вопрос: как же так, мы, вместе с окружающими нас объектами, являемся частью Вселенной, при этом классически взаимодействуем с окружением и вовсе не находимся в нелокальном состоянии. Как это сопоставить с тем, что было сказано выше? Никакого противоречия здесь нет, и квантовая механика также отвечает на этот вопрос. Кстати, отвечая на него, ученые вывели количественную характеристику запутанности. Все дело в том, что мы, вместе с окружающими нас объектами, являемся именно частью системы, а классические корреляции отсутствуют во всей системе целиком. То есть в пространстве состояний (гильбертовом пространстве) с максимальной размерностью, соответствующем всей системе, классических корреляций нет, но они могут быть между подсистемами в пространствах состояний меньшей размерности. Данное обстоятельство можно пояснить еще следующим образом: гипотетический внешний наблюдатель, который смотрит на замкнутую систему снаружи, не увидит перед собой никаких классических объектов и не обнаружит взаимодействий между ними. Перед ним будет пустота – уточню: это в том случае, если наблюдатель охватывает взглядом сразу всю систему. Если же у него есть что-то наподобие «подзорной трубы», и через нее он станет смотреть на отдельную подсистему, «вырезая» из поля зрения все остальное окружение, тогда он уже сможет увидеть выделенную подсистему как классический локальный объект.

Если обратиться к математическому формализму квантовой теории, то для записи вектора состояния обычно используют дираковские обозначения. В самом простом случае двухуровневой системы (например, кубита), вектор состояния имеет вид:

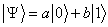, (2.1)

где а и b – комплексные числа, которые могут принимать любые значения, удовлетворяющие условию нормировки | а |² +| b |² =1. Можно сказать, что кубит с вероятностью | а |² находится в состоянии |0ñ и с вероятностью | b |² – в состоянии |1ñ. Это обобщение классического бита, который является предельным случаем кубита при | а |² = 1, либо | b |² = 1.

Состояние |0ñ = |↑ñ = (1, 0)^Т – это вектор-столбец (спин-вверх); состояние |1ñ = |↓ñ = (0, 1)^Т тоже вектор-столбец, но спин-вниз.

Дата добавления: 2015-03-29