Контрольные примеры

Просчеты по программе queennum (n) при разных значениях n приводят к следующим результатам:

n
Число расстановок

Для формулировки следующей задачи введем одно понятие. Среди всех расстановок n ферзей на доске n ´ n выделим отдельные непересекающиеся классы H_s (s = 0, 1,..., q) расстановок так, что все элементы данного класса можно получить из любого его представителя какими-либо элементарными преобразованиями типа:

	поворот доски в её плоскости вокруг центра на 90^0, 180^0 и 270^0;
	преобразования симметрии относительно диагоналей;
	преобразования симметрии относительно прямых, проходящих через центр доски по границам клеток.

Взяв по одному представителю из каждого класса H_s (s = 0, 1,..., q), получим некоторое множество, называемое основными расстановками.

адача 3. Основные расстановки. Составить рекурсивную программу-функцию, находящую какое-либо множество основных расстановок n ферзей на шахматной доске размера n ´ n.

Решение. Эта задача решается с помощью функций quaf (), qua () и sift () практически тем же самым способом, что и задача 1. Отличия здесь такие. Рекурсивная функция qua (), как и функция qu () задачи 1, последовательно формирует каждую из возможных расстановок ферзей на доске, но не все из них запоминаются в матрице ответа ot. Очередная, полученная в qua (), расстановка pos в функции sift () подвергается проверке - включать или не включать её в матрицу ot. Делается это следующим образом. Из вектора pos описанными выше элементарными преобразованиями формируются еще семь расстановок (некоторые из них могут оказаться совпадающими). Если ни одна из них не входит в текущую матрицу ответов ot, то ot дополняется новым решением pos и т.д. Следовательно, по завершении вычислений ot будет содержать некоторое множество основных расстановок.

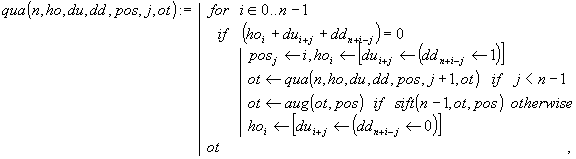
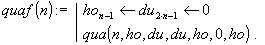
Задание.

1. Реализовать программное решение задачи «Ханойские башни»

2. Реализовать программное решение задачи «Расстановка ферзей на шахматной доске».

Дата добавления: 2015-05-06