Анализ электрических цепей

Методические указания по разделам курса

Электрические цепи постоянного тока. Электрическая цепь - это совокупность устройств, предназначенных для получения, передачи и преобразования в другие виды электрической энергии. Она состоит из источника и приемника электрической энергии, связанных соединительными проводами. Кроме этих элементов цепь включает в себя коммутационно-защитную аппаратуру и электроизмерительные приборы. Эти устройства служат для управления и контроля за работой цепи, а также для защиты ее элементов от перегрузок.

Основной задачей анализа электрических цепей является определение токов всех ветвей при заданной конфигурации цепи и известных параметрах всех ее элементов. При расчете токов часто изображают не реальную цепь, а ее схему замещения. Схема замещения - это графическое изображение реальной цепи с помощью идеальных элементов, параметрами которых являются параметры реальных элементов, входящих в цепь. На схеме замещения не указывают измерительные приборы, аппаратуру защиты и аппаратуру включения-выключения.

На схеме замещения различают ветви, узлы и контуры. Ветвь - это участок цепи, в любом сечении которого течет один и тот же ток. Узел - это точка, в которой сходится не менее трех ветвей. Контур - любой замкнутый путь для электрического тока.

Контур называется независимым, если он имеет хотя бы один элемент, принадлежащий только ему.

Элементы цепи могут включаться последовательно и параллельно. При последовательном включении во всех элементах протекает один и тот же ток. При параллельном включении элементы цепи подключаются к одной паре узлов.

Для расчета токов в ветвях цепи применяют законы Кирхгофа и Ома.

Первый закон Кирхгофа относится к узлу и гласит:

алгебраическая сумма токов, сходящихся в узле, равна нулю.

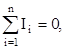
где i - номер тока;

n - количество токов, сходящихся в узле.

Второй закон Кирхгофа относится к контуру, он гласит:

алгебраическая сумма ЭДС, действующих в контуре, равна алгебраической сумме падений напряжений в том же контуре.

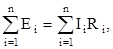
где i - номер ветви контура;

n - число ветвей, входящих в контур.

Законы Кирхгофа применяют для расчета сложных разветвленных цепей, включающих в себя несколько источников энергии. При этом необходимо составить p = m + (n-1) уравнений, где m - число независимых контуров, n - число узлов.

При расчете рекомендуется придерживаться следующей последовательности:

Выбрать направление обхода контуров (ошибок в дальнейшем будет меньше, если направление будет во всех контурах одинаковым).

Произвольно указать направление токов в ветвях цепи.

Составить необходимые уравнения по первому закону Кирхгофа.

Составить необходимые уравнения по второму закону Кирхгофа, считая положительными токи и ЭДС, совпадающие с направлением обхода контура.

Решить полученную систему уравнений любым известным методом.

Провести проверку правильности решения путем составления баланса мощностей.

Пример решения 1.

Для электрической цепи, изображенной на рис. 1.1., по данным значениям ЭДС источников и сопротивлениям резисторов найти величины токов во всех ветвях и их направления.

Е₁=45 В; Е₂=60 В; R₀₁=0,1 Ом; R₀₂=0,15 Ом; R₁=R₂=R₅=2 Ом; R₃=10 Oм; R₄= 4 Ом.

Так как резисторы R₁, R₅ и R₄ включены последовательно, то I₄=I₅=I₁; аналогично I₃=I₀₂=I₂.

На основании первого закона Кирхгофа для узла “а” имеем I₁+I₀₁-I₂=0.

На основании второго закона Кирхгофа для контура R₁-R₅-R₄-Е₁- R₀₁-R₁ получаем I₁(R₁+R₅+R₄)-I₀₁R₀₁=-E₁.

Аналогично, для контура R₂-R₀₁ -Е₁- R₃- Е₂-R₀₂-R₂:

I₂(R₃+R₀₂+R₂)+I₀₁R₀₁=E₁- Е₂.

Подстановка значений ЭДС и сопротивлений дает систему уравнений:

I₁+I₀₁-I₂=0

8I₁-0,1I₀₁+0I₂=-45

0I₁+0,1I₀₁+12,15I₃=-15

Решение системы уравнений дает:

I₁=-5,57 A, I₀₁=4,30 A, I₂=-1,27 A.

Отрицательные значения токов I₁ и I₂ означают, что первоначально их направления были выбраны неверно и их направления на схеме надо сменить на противоположные.

Для проверки правильности решения необходимо составить баланс мощностей

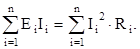
Произведение E_iI_i берется со знаком “+”, если направления ЭДС и тока в ветви “i” совпадают. E₁I₀₁+E₂I₂=I₁²(R₁+R₅+R₄)+I₂²(R₃+R₀₂+R₂)+I₀₁²R₀₁. Подстановка значений ЭДС, токов и сопротивлений и расчет дают: 269,7=269,7, т.е. задача решена верно.

При расчете сложных цепей с большим количеством источников энергии рациональнее использовать метод контурных токов, позволяющий почти вдвое сократить количество уравнений.

В методе контурных токов независимыми переменными являются контурные токи, условно замыкающиеся по элементам независимых контуров.

Чтобы найти контурные токи каждого независимого контура, необходимо составить уравнения второго закона Кирхгофа и решить полученную систему линейных уравнений. При расчете рекомендуется придерживаться следующей последовательности:

Выделить все независимые контуры.

Указать направления обхода контуров (лучше, если направления обхода всех контуров будет одним и тем же).

Указать направления контурных токов в каждом контуре (чтобы избежать ошибок при составлении уравнений, рекомендуется направления контурных токов выбирать совпадающими с направлениями обхода).

Для всех независимых контуров составить уравнения второго закона Кирхгофа.

Решить полученную систему уравнений.

Произвести проверку правильности ее решения.

По вычисленным значениям контурных токов определить величины токов в ветвях и их направления.

Составить баланс мощностей.

Рассмотрим решение на примере предыдущей задачи (рис.1.2.).

По признакам, данным в определении независимого контура, можно выделить следующие независимые контуры: R₁-R₅-R₄-E₁-R₀₁-R₁ и R₂-R₀₁-E₁-R₃-E₂-R₀₂-R₂. В соответствии с выбранными направлениями обхода и контурных токов запишем уравнения второго закона Кирхгофа

I_k1(R₀₁+R₁+R₅+R₄)-I_k2R₀₁=-E₁

-I_k1R₀₁+I_k2(R₀₁+R₃+R₀₂+R₂)=E₁-E₂.

Подстановка значений сопротивлений и ЭДС и решение полученной системы уравнений дает: I_к1=-5,57 А, I_к2=-1,27 А.

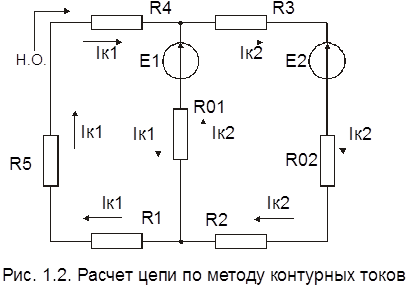Так как в наружной ветви R₁-R₅-R₄ протекает только контурный ток I_к1, то I₁=I₄=I₅=5,57 A, а направление их противоположно направлению I_к1. Аналогично I₂=I₃=1,27 A.

В ветви R₀₁-E₁ протекают два контурных тока в противоположных направлениях, поэтому для нахождения тока I₀₁ необходимо из большего контурного тока вычесть меньший и принять направления большего, т.е.

I₀₁=I_k2-I_k1=-1,27-(-5,57)=4,3 A.

Баланс мощностей составляется как в предыдущей задаче.

Цепи с одним источником энергии можно рассчитать, пользуясь только законом Ома путем эквивалентного преобразования цепи.

Пример решения 2.

Рассмотрим расчет на примере цепи, представленной на рис. 1.3.

Для цепи, представленной на рис. 1.3, найти токи во всех ветвях, определить ЭДС источника Е и показания приборов, если: R₀=0,15 Ом; R₁=0,7 Oм; R₂=40 Ом; R₃=8 Ом; R₄=4 Ом; R₅=2,4 Ом; R₆=4 Ом; I₂=0,25 А.

Решение.

1. В соответствии с положительным направлением ЭДС-Е укажем направления токов во всех ветвях.

2. По закону Ома для участка цепи найдем напряжение на резисторе R₂

U₂=I₂R₂=0,25*40=10 В.

3. Так как R₃ и R₂ подключены к одной паре узлов a-b, то напряжение на резисторе R₃ равно U₂, и тогда I₃ можно найти по закону Ома для участка цепи.

4. На основании первого закона Кирхгофа для узла”b” имеем:

I_А=I₂+I₃=0,25+1,25=1,5 A.

5. Если сопротивлением амперметра пренебречь, то напряжение на участке R₄-R₅ будет равно U₂ и тогда

6. На основании первого закона Кирхгофа для узла “a” можно записать:

I₆=I₂+I₃+I₄=0,25+1,25+1,56=3,06 A.

7. На участке R₁-R₀-E-R₆ все элементы включены последовательно и тогда

I₆=I₁=3,06 А.

8. Напряжение на резисторе R₆ найдем на основании закона Ома

U₆=I₆R₆=3,06*4=12,24 B.

9. На основании второго закона Кирхгофа показание вольтметра Uv=U₆+U₂=12,24+10=22,24 B.

10. На основании второго закона Кирхгофа ЭДС источника

E=I₁R₀+I₁R₁+U_ad=3,06*0,15+3,06*0,7+22,24=24,84.

Проверка правильности решения осуществляется по балансу мощностей как указано ранее.

Электрические цепи переменного тока. Ток, величина и направление которого изменяются во времени, называется переменным. Из всего многообразия переменных токов наибольшее распространение получил ток, изменяющийся по синусоидальному закону. Синусоидальные токи возникают в цепях под действием синусоидальных ЭДС и напряжений.

Значение синусоидального тока в данный момент времени называется мгновенным (обозначается i).

Максимальное значение синусоидального тока называется амплитудным (обозначается I_m).

Действующим значением синусоидального тока называется такой постоянный ток, который за время одного периода выделяет такое же количество тепла, что и данный переменный ток (обозначается I). В действующих значениях градуированы вольтметры и амперметры. Действующие и амплитудные значения связаны следующим соотношением:

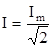
При анализе электрического состояния цепей расчет токов ведут либо для действующих, либо для амплитудных значений. Наиболее общим методом расчета цепей синусоидального тока является символический. В этом случае синусоидальная величина изображается вращающимся вектором, положение которого на комплексной плоскости в данный момент времени описывается комплексным числом (символом).

Существует три формы записи комплексного числа: алгебраическая, показательная и тригонометрическая.

В алгебраической форме комплексное число записывается в виде многочлена, например

A =a+jb,

где a - проекция вектора на ось действительных величин;

b - проекция вектора на ось мнимых величин;

j - мнимая единица.

Алгебраическая форма записи удобна для сложения и вычитания комплексных чисел.

В показательной форме комплексное число записывается в виде

A =Ae^jj,

где - модуль комплексного числа.

j=arctg b/a - угол, образуемый вектором с положительным направлением оси действующих величин.

Показательная форма записи удобна для умножения и деления комплексных чисел.

В тригонометрической форме комплексное число записывается в виде многочлена

A =ACosj+jASinj.

Тригонометрическая форма записи позволяет легко перейти от показательной формы записи к алгебраической. При символическом расчете все уравнения для цепей постоянного тока остаются справедливыми и для цепей переменного тока с той только разницей, что все величины, входящие в них, берутся в комплексной форме.

Пример решения 3.

Для цепи, изображенной на рис. 1.4., по данным значениям напряжения и сопротивлений определить показания приборов, а также полную и реактивную мощности, построить векторную диаграмму.

Начальную фазу напряжения принимают равной нулю, тогда комплекс приложенного напряжения будет равен

U =127 e^jo В.

Комплекс полного сопротивления последовательно соединенных элементов R, L и C

Z =R+j(X_L-X_c).

Отсюда комплексы полного сопротивления ветвей

Z ₁=jX_L1=j5=5e^j90 Ом

Z ₂=R₂-jX_c2=3-j4=5e^-j53 Ом.

По закону Ома определяют комплексы токов в ветвях

I ₁= U / Z ₁=127e^j0/(5e^j90)=25,4e^-j90= -j25,4 A.

I ₂= U / Z ₂=127e^j0/(5e^-j53)=25,4e^j53 A.

По первому закону Кирхгофа находят ток в неразветвленной части цепи

I = I ₁+ I ₂=16,3e^-j19 A..

Определяют комплексную мощность цепи. Комплексной мощностью S называется произведение комплекса напряжения на сопряженный комплекс тока I^*. Сопряженные комплексы: ; .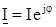

Действительная часть комплексной мощности есть активная мощность Р, а мнимая часть - реактивная мощность Q.

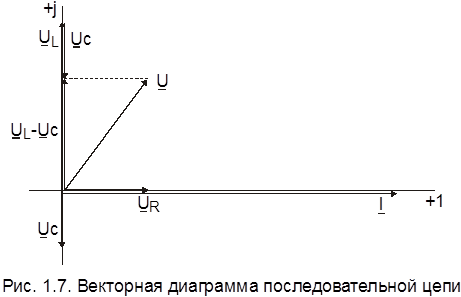
Построение векторной диаграммы начинают с выбора масштаба по току и напряжению.

В выбранных масштабах откладывают векторы напряжения и токов в соответствии с рассчитанными значениями. Отсчет углов ведут от оси +1. Положительные углы откладывают в направлении, противоположном движению часовой стрелки. Вектор тока в неразветвленной части цепи находят сложением векторов тока I ₁ и I ₂.

Пример решения 4.

В цепи, представленной на рис.1.6., действует напряжение u=U_mSinwt, частотой 50 Гц. Найти показания приборов, реактивную и полную мощности, построить векторную диаграмму, если U_m=282 B, R=3 Ом, L=19,1 мГн, С=1592,4 мкФ.

Решение.

1. Так как вольтметр градуирован в действующих значениях, напряжение на зажимах цепи будет равно:

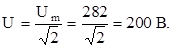
2. Реактивное сопротивление индуктивности L

X_L=2pfL=

Комплекс индуктивного сопротивления

jX_L=j6=6e^j90 Ом.

3. Реактивное сопротивление емкости С

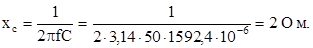
Комплекс емкостного сопротивления

-jX_c=-j2=2e^-j90 Ом.

4. Комплекс полного сопротивления цепи

Z =R+j(X_L-X_c)=3+j(6-2)=3+j4=5e^{j arctg4/3}=5e^j53 Ом.

5. Начальную фазу напряжения, приложенного к зажимам цепи, принимают равной нулю, тогда комплекс напряжения на зажимах цепи

U =200e^jo B.

6. Комплекс тока находится по закону Ома

I = U / Z =200e^j0/(5e^j53)=40e^-j53 A.

Показание амперметра I_A=40 A.

7. Комплекс напряжения на участке R

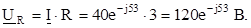
Показание вольтметра на участке R

U_R=120 B.

8. Комплекс напряжения на участке L

U _L= I jX_L=40e^-j536e^j90=240e^j37 B.

Показание вольтметра на участке L

U_L=240 B.

9. Комплекс напряжения на участке С

U _c= I(-j X_c)=40e^-j532e^-j90=80e^-j143 B

Показание вольтметра на участке С

U_C=80 B.

10. Комплексная полная мощность цепи:

Полная мощность S=8000 ВА.

Действительная часть комплексной полной мощности есть показание ваттметра

Р=4814,5 Вт.

Мнимая часть комплексной полной мощности есть мощность реактивная

Q=6389 Вар.

11. Разность фаз между напряжением и током:

j=j_U- j_I=0-(-53)=53⁰.

12. Показание фазометра

Cosj=Cos53= 0,602.

При построении векторной диаграммы в выбранных масштабах тока и напряжения строят векторы тока и напряжений, комплексы которых рассчитаны. Положительные углы отсчитываем от оси действительных величин в направлении, противоположном движению часовой стрелки.

Вектор напряжения, приложенного к зажимам цепи, находится путем сложения U _R, U _L и U _c по правилам сложения векторов.

Трехфазные электрические цепи. Совокупность электрических цепей, в которых одним источником энергии создаются три синусоидальные электродвижущие силы одинаковой частоты и амплитуды, векторы которых сдвинуты относительно друг друга на угол 120⁰, называется трехфазной системой или трехфазной цепью. Каждая из цепей, входящих в трехфазную систему, называется фазой; обозначения фаз - А, В,С. Токи, протекающие в фазах приемника, называются фазными.

Трехфазные приемники могут быть включены звездой или треугольником; они могут быть симметричными или несимметричными. Приемник называется симметричным, если комплексы полных сопротивлений его фаз равны, т.е. Z _a= Z _b= Z _c.

Звезда - это такое соединение, при котором концы фаз, обозначаемые буквами x, y, z, соединяются в один узел, который называется нейтральной точкой, а начала фаз, обозначаемые буквами a, b, c, соединяются с источником. Нейтральная точка приемника соединяется с нейтральной точкой источника.

Провода, соединяющие начала фаз приемника и источника, называются линейными; в них протекают линейные токи. Провод, соединяющий нейтральные точки, называется нейтральным, или нулевым.

Треугольник - это такое соединение, при котором конец предыдущей фазы соединяется с началом последующей.

Одним из достоинств трехфазных систем является наличие двух рабочих напряжений - фазного и линейного.

Фазным напряжением называется напряжение между началом и концом одной и той же фазы.

Линейным напряжением называется напряжение между началами двух фаз.

Для приемников, включенных по схеме ”звезда” с нейтральным проводом, выполняются следующие соотношения:

I_л=I_ф U_л= .

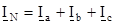Ток в нейтральном проводе может быть найден также из векторной диаграммы.

Для приемников, включенных по схеме “треугольник”, выполняются соотношения:

U_л=U_ф I_л= .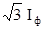

Однако, если приемник несимметричный, линейные токи указанному соотношению не подчиняются и могут быть найдены либо аналитически, как разности комплексов фазных токов

, , ,

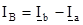либо из векторной диаграммы.

Здесь , , - комплексы токов в линейных проводах;

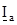, , - комплексы фазных токов в фазах приемника.

При расчете комплексов токов в фазах приемника, они определяются отдельно для каждой фазы на основании закона Ома.

I _a= U _a/ Z _a; I _b= U _b/ Z _b; I _c= U _c/ Z _c.

Здесь , , - комплексы фазных напряжений,

Z _a, Z _b, Z _c - комплексы полных сопротивлений фаз.

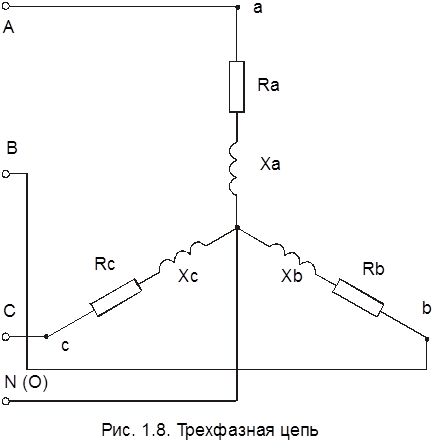
Пример решения 5.

Для активно-индуктивного приемника, включенного по схеме “звезда” с нейтральным проводом (рис.1.8.) в сеть с линейным напряжением U_л=380 В, найти фазные и линейные токи, а также ток в нейтральном проводе, активные мощности отдельных фаз и активную мощность приемника, если R_a=3 Ом, R_b=4 Ом, R_с=6 Ом, X_а=4 Ом, X_b=3 Ом, X_с=8 Ом.

1. Находят действующее значение фазного напряжения

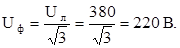
2. Начальную фазу напряжения в фазе “а” принимают равной нулю, тогда комплексы фазных напряжений будут:

; ; .

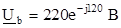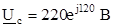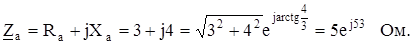3. Определяют комплексы полных сопротивлений фаз приемника

.

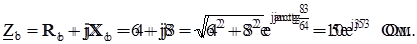4. Вычисляют комплексы фазных токов

I _a= U _a/ Z _a=220e^j0/(5e^j53)=44e^-j53 A.

I _b= U _b/ Z _b=220e^-j120/(5e^j37)=44e^-j157 A.

I _c= U _c/ Z _c=220e^j120/(10e^j53)=22e^j67 A..

5. Так как приемник включен “звездой”, линейные токи равны фазным.

; ; .

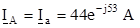6. Находят ток в нейтральном проводе

Действующее значение тока в нейтральном проводе:

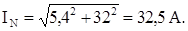
7. Определяют комплексные полные мощности фаз приемника

Активная мощность фазы “а”: Р_а=5825 Вт.

Реактивная мощность фазы “а”: Q_а=7730 Вар.

Активная мощность фазы “b”: Р_b=7730 Вт.

Реактивная мощность фазы “b”: Q_b=5825 Вар.

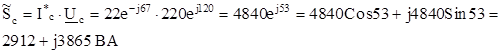
Активная мощность фазы “c”: Р_c=2912 Вт.

Реактивная мощность фазы “c”: Q_c=3865 Вар.

8. Вычисляют активную мощность приемника.

Активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз.

Р=Р_а+Р_b+Р_c=5825+7730+2912=16469 Вт.

Для удобства построения векторной диаграммы поворачивают оси координат на 90⁰ в направлении, противоположном движению часовой стрелки.

В выбранном масштабе откладываются векторы фазных напряжений. Векторы фазных напряжений строят в соответствии с расчетными значениями комплексов фазных токов. Положительные углы откладывают в сторону, противоположную движению часовой стрелки, от оси действительных величин. Вектор тока в нейтральном проводе находится сложением векторов фазных токов по правилам сложения векторов.

Дата добавления: 2015-05-06