Зависимость «длина — сила»

Зависимость «частота — сила».

Даже при очень высоких частотах стимуляции миокард рабо­тает в режиме одиночных сокращений и не способен к развитию тетануса (суммированного сокращения), характерного для ске­летной мышцы. Такая особенность миокарда является следствием длительного рефрактерного периода кардиомиоцитов и защища­ет сердце от преждевременных возбуждений и утомления. Одна­ко еще в XIX в. американский физиолог X. Боудич в экспери­ментах с электростимуляцией изолированного сердца наблюдал увеличение силы сердечных сокращений при увеличении частоты стимуляции. Указанная особенность зависимости «частота—си­ла» получила название «лестницы Боудича», или хроноинотропного эффекта (от греч. chronos — время, inos –сила).

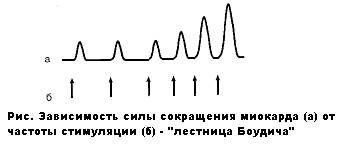
Возникновение хроноинотропного эффекта, возможно, связано с тем, что при высокой частоте стимуляции промежутки времени между сокращениями укорачиваются, вследствие чего не проис­ходит полного удаления ионов Са⁺⁺, поступивших в саркоплазму при очередном сокращении. В результате с каждым последующим сокращением концентрация внутриклеточного ионизированного Са⁺⁺ возрастает и соответственно возрастает сила сокращений.

В 1895 г. О. Франк показал, что, как и для скелетной мышцы, сила сокращения миокарда тем больше, чем больше степень предшествующего растяжения мышечных волокон. При растяжении саркомера происходит выдвижение актиновых и миозиновых ни­тей из промежутков между ними. Соответственно увеличивается количество актомиозиновых мостиков, которые могут образо­ваться при сокращении, а значит, возрастает и потенциальный резерв увеличения силы сокращения. Максимальная сила сокра­щения достигается при исходной длине саркомера около 2,2 мкм. Зависимость силы сокращения от степени предварительного рас­тяжения миокарда лежит в основе закона Франка—Старлинга («закона сердца»).

Зависимость «скорость — сила (нагрузка)».

Режим сокращения мышцы с постоянной силой (при посто­янной нагрузке) называется изотоническим (от греч. isos — рав­ный, tonos — напряжение). При этом чем больше нагрузка, темменьше скорость сокращения. Зависимость скорости сокращения от нагрузки для миокарда, как и для скелетной мышцы, описывается уравнением Хилла:

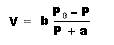
где V — скорость сокращения, см/с; Р — сила мышечного сокра­щения (нагрузка), гс; Р₀ — максимальная возможная сила сокра­щения; а — константа, которая характеризует тепло, выделяю­щееся при укорочении мышцы, и зависит от КПД работы мышцы; b — константа, характеризующая скорость перехода химической энергии в механическую (константы а и b имеют соответственно размерности нагрузки и скорости).

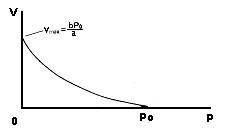
Рис. Зависимость скорости сокращения волокон сердечной мышцы (V) от нагрузки (Р)

По оси ординат: скорость сокращения, см/с. По оси абсцисс: нагрузка (г). Максимальная скорость сокращения V_max по­зволяет судить о сократимости миокарда, так как она пропорциональна макси­мальной силе сокращения (Ро). При Р = Ро (максимальная нагрузка) укорочение сердечной мышцы отсутствует — состояние максимального изометрического со­кращения (напряжения).

На рис. представлен график зависимости «скорость—на­грузка», из которого следует, что если нагрузка на мышцу равна нулю (Р = 0), то скорость ее сокращения максимальна и равна V_max = bP₀/a. Так как в сердечной мышце величина b/а является относительно постоянной, оценка максимальной скорости сокра­щения позволяет судить о сократимости миокарда. Второму крайнему случаю, когда нагрузка на мышцу макси­мальна (Р = Ро) и укорочение отсутствует, соответствует состоя­ние максимального изометрического сокращения (напряжения). Следует отметить, что классического изометрического сокраще­ния (от греч. isos — равный, metron — мера, размер), при котором длина мышечных волокон остается постоянной, в интактном серд­це не наблюдается. Даже при неизменном объеме камер сердца происходит внутреннее укорочение центральных и одновременное растяжение периферических участков сердечной мышцы. Кроме того, при сокращении сердца его стенки подвергаются де­формации, что приводит к изменению длины мышечных волокон.

Следует различать термины «сила сердечных сокращений» и «сократимость (или инотропное состояние) миокарда». По мне­нию американского физиолога С. Сарнова, который ввел понятие «сократимость миокарда», этот термин характеризует внутрен­ние свойства сердечной мышцы, определяющие способность сердца к выполнению работы по перекачиванию крови. На кле­точном уровне эта способность определяется состоянием сокра­тительного аппарата кардиомиоцитов: концентрацией внутрикле­точных ионов Са^{+ +}, чувствительностью к ним миофибрилл, ин­тенсивностью метаболизма. Таким образом, об изменениях со­кратимости миокарда свидетельствуют только такие изменения силы и скорости сердечных сокращений, которые не связаны, в частности, с увеличением исходной длины волокон миокарда, т. е. осуществляются без участия механизма Франка—Старлинга.

Дата добавления: 2015-05-06