ИДЗ-2. Законы алгебры множеств

ИДЗ-1. Основные понятия теории множеств

Методические указания к решению задач

Введение

Часть 1

Екатеринбург – 2011

Настоящая методическая разработка предназначена для студентов всех форм обучения, изучающих дисциплину «Математические основы обработки информации». Разработка содержит индивидуальные домашние задания (ИДЗ) по 30 вариантов в каждом и методические указания к их решению.

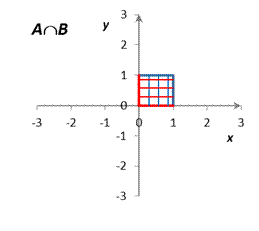
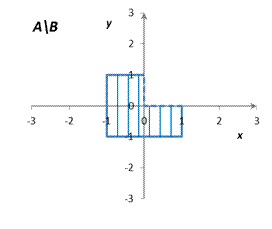
Определить и изобразить на рисунках множества A, B, A È B, A Ç B, A / B, B / A, A D B, где

A = {(x, y) Î R ²: | x | £ 1, | y | £ 1},

B = {(x, y) Î R ²: | x – 1| £ 1, | y – 1| £ 1}.

Решение: Множества A и B представляют собой множества точек на декартовой плоскости R ´ R = R ² (плоскости Oxy). Как нетрудно установить, множество A представляет собой внутренность квадрата с центром в точке (0; 0) со сторонами длиной 2, параллельными координатным осям; граница принадлежит множеству A. Аналогично, множество B представляет собой внутренность квадрата с центром в точке (1; 1) со сторонами длиной 2, параллельными координатным осям; граница принадлежит множеству B. Множества A, B, A È B, A Ç B, A / B, B / A, A D B изображены на рис. 1.

Пусть A, B, C – подмножества некоторого универсального множества U. Установите справедливость нижеследующего утверждения:

(A \ B)È(B \ A) = (A È B)\(A Ç B).

Решение: Разложим множества A и B на непересекающиеся подмножества { x_A }, { x_B }, { x_AB }:

A = { x_A È x_AB };

B = { x_B È x_AB }.

В этих обозначениях для левой части предполагаемого равенства имеем:

A \ B = { x_A È x_AB }\{ x_B È x_AB } = { x_A };

B \ A = { x_B È x_AB }\{ x_A È x_AB } = { x_B };

(A \ B)È(B \ A) = { x_A }È{ x_B } = { x_A È x_B }.

Для правой части равенства имеем:

A È B = { x_A È x_AB }È{ x_B È x_AB } = { x_A È x_B È x_AB };

A Ç B = { x_A È x_AB }Ç{ x_B È x_AB } = { x_AB };

(A È B)\(A Ç B) = { x_A È x_B È x_AB }\{ x_AB } = { x_A È x_B }.

Левая и правая части доказываемого равенства одинаковы и равны { x_A È x_B }. Справедливость утверждения установлена.

	Рис. 1

Дата добавления: 2015-03-29