Определение параметров постоянных рент постнумерандо

Как было показано выше, постоянная рента описывается набором основных параметров — R, n, i и дополнительными параметрами p, m. Однако при разработке контрактов и условий финансовых операций могут возникнуть случаи, когда задается одна из двух обобщающих характеристик S или A и два основных параметра. Необходимо рассчитать значение недостающего параметра.

Определение члена ренты. Исходные условия: задается S или A и набор параметров, кроме R. Например, за обусловленное число лет необходимо создать фонд в сумме S путем систематических постоянных взносов. Если принято, что рента должна быть годовой, постнумерандо, с ежегодным начислением процентов, то, обратившись к формуле (4.6), получим:

R = S / s_n;i. (4.24)

Аналогичным путем на основе зависимостей (4.7) — (4.12) легко получить формулы для расчета членов рент с другими условиями.

Пусть теперь известна (задана условиями договора) современная стоимость ренты. Если рента годовая, постнумерандо, m = 1, то из формулы (4.14) следует:

R = A / a_n;i. (4.25)

Наоснове формул (4.16) — (4.21) нетрудно определить R и для других условий ренты.

Пример 4.12. Определим размеры периодических взносов при решении двух следующих задач:

а) создать целевой фонд (например, для погашения задолженности или обеспечения инвестиций) в сумме 100 млн. руб.;

б) погасить в рассрочку текущую задолженность в сумме 100 млн. руб.

Срок в обоих случаях пять лет, процентная ставка равна 20%, платежи ежегодные постнумерандо.

а) S = 100, R = S / s _5;20 = 100/7,4416 = 13,438 млн. руб.;

б) A = 100, R =A/a _5;20 = 100 / 2,9906 = 33,438 млн. руб.

Расчет срока ренты. Иногда при разработке контракта возникает необходимость в определении срока ренты и соответственно числа членов ренты. Решая полученные выше выражения, определяющие S или A, относительно n, получим искомые величины. Так, для годовой ренты с ежегодным начислением процентов находим:

Таблица 4.1 Формулы для расчета срока постоянных рент постнумерандо

Количество платежей в году	Количество начислений в году	Сроки платежей
S	A
p = 1	m = l		(4.26)		(4.27)
m > 1		(4.28)		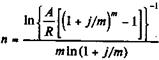(4.29)
p >1	m = l		(4.30)		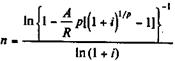(4.31)
m = p		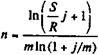(4.32)		(433)
m ≠ p		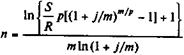(4.34)		(4.35)

Аналогичным образом получим формулы для расчета срока и для других видов рент. Формулы, полученные для дискретных процентов, приведены в табл. 4.1.

Для рент с непрерывным начислением процентов находим на основе формул (4.11), (4.12) и (4.20), (4.21):

для годовой ренты

(4.36)(4.37)

для p -срочной ренты

. (4.38)(4.39)

Все приведенные выше формулы для определения n, естественно, пригодны и в случаях, когда заданными являются коэффициенты приведения или наращения рент, поскольку a_n;i = A/R, s_n;i = S/R и т. д.

При расчете срока ренты необходимо принять во внимание следующие моменты:

1. Расчетные значения срока будут, как правило, дробные. Необходимо округление результата. В этих случаях для годовой ренты в качестве n часто удобнее принять ближайшее меньшее целое число. У p -срочной ренты результат округляется до ближайшего целого числа периодов — np. Например, пусть для квартальной ренты получено n = 6,28 года, откуда np = 25,12 квартала. Округляем до 25, в этом случае n = 6,25 года.

2. Если округление производится до меньшего целого числа, то наращенная сумма или современная стоимость ренты с таким сроком оказывается меньше заданной. Возникает необходимость в соответствующей компенсации. Например, если речь идет о погашении задолженности путем выплаты постоянной ренты, то компенсация может быть осуществлена соответствующим платежом в начале или конце срока либо с помощью повышения суммы члена ренты.

Обсудим еще одну проблему, связанную со сроком ренты. Пусть A — текущее значение долга. Если он погашается с помощью постоянной ренты, то из формулы (4.14) следует, что долг может быть погашен за конечное число лет только при условии, что R > Ai. Аналогичные неравенства можно найти и для других видов рент. Если условия ренты таковы, что имеет место равенство, например R = Ai, то n = , т. е. рента окажется вечной и долг практически не может быть погашен. Если же R < Ai, то долг систематически увеличивается.

Пример 4.13. Какой необходим срок для накопления 100 млн. руб. при условии, что ежемесячно вносится по 1 млн. руб., а на накопления начисляются проценты по ставке 25% годовых? Имеем R = 12, i = 25%. По формуле (4.30) находим:

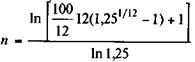= 4,7356 года.

Если срок округляется до пяти лет, то необходимо несколько уменьшить размерчлена ренты, т.е. найти член ренты для n = 5. В этом случае ежемесячный взносдолжен составить 914,79 тыс. руб. — см. формулу (4.25).

Определение размера процентной ставки. Необходимостьв определении величины процентной ставки возникаетвсякий раз,когда речь идет о выяснении эффективности (доходности) финансово-банковской операции. Заметим, что расчет процентной ставки по остальным параметрам ренты не так прост, как это может показаться на первый взгляд. В простейшем случае задача ставится следующим образом: решить уравнение (4.4) или (4.14) относительно i. Нетрудно убедиться в том, что алгебраического решения нет. Для получения искомой величины без применения компьютера с соответствующим пакетом программ прибегают к линейной интерполяции или какому-либо итерационному методу, например методу Ньютона — Рафсона, методу секущей и т. д.. При небольших значениях i можно применить разложение бинома Ньютона и использовать два-три первых члена разложения.

Линейная интерполяция. По заданным R, S или A находят значения коэффициентов наращения или приведения ренты:

s_n;i = S/R; a_n;i = A/R.

Для оценки i применяется следующая интерполяционная формула:

(4. 40)

где a_в и a_н - значениякоэффициентов наращения или приведения рент для верхнего и нижнего значенияставок (ставки i_в, i_н);

a — значениекоэффициента наращения или приведения, для которого определяется размер ставки.

На рис. 4.3 и 4.4 изображены зависимости соответствующих коэффициентов от размера процентной ставки, а также интерполяционные оценки и точные их значения. Первые обозначены как i, вторые — как i".

Как видно из рисунков, оценки размера процентной ставки несколько отличаются от точных значений этой величины, причем если за основу взят коэффициент приведения, то оценка оказывается завышенной₎ в свою очередь оценка i по коэффициенту наращения меньше точного значения. Чем меньше диапазон i_н — i_в тем точнее оценка процентной ставки.

Пример 4.14. Допустим, что предполагается путем ежегодных взносовпостнумерандо по 100 млн. руб. в течение семи лет создатьфонд в размере 1 млрд. руб. Какова должна быть годовая процентная ставка?

Определим исходный коэффициент наращения:

s _{7; i} = 1000/100 = 10.

Для начала предположим, что искомая процентная ставка находится в интервале 11 - 12%. Для этих значенийставки находим коэффициент наращения: a_в = s _7;12 = 10,08901, a_н = s _7;11 = 9,78327.

Отсюда

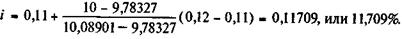
Проверка: по формуле (4.5) находим s _7;11,709 = 9,999. Таким образом, найденное значение ставки обеспечивает выполнение поставленных условий почти точно.

Метод Ньютона — Рафсона. Как известно, с помощью этого метода последовательным приближением решается нелинейное уравнение f (x) = 0. Общий вид рекуррентного соотношения:

x_{k +1} = x_k - f (x_k)/ f' (x_k), (4.41)

где k — номер итерации.

Основная задача заключается в разработке функции f (x), удобной для дальнейших выкладок. Обсудим сначала вариант постановки задачи, когда в качестве заданной принимается сумма накоплений S, рента годовая, постнумерандо. На основе формулы (4.4), приняв q = 1 + i, получим:

Преобразуем эту функцию и найдем ее производную.

Вместо общей записи рекуррентного соотношения (4.41) теперь можно написать:

q_{k +1} = q_k - f (q_k)/ f' (q_k). (4.42)

Начальное значение q выбирают так, чтобы s_n;i было близко к заданной величине отношения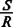

Аналогичным путем находим функцию и ее производную для случая, когда заданной является современная стоимость ренты. Функция имеет вид:

Отсюда для годовой ренты получим:

В свою очередь для p -срочной ренты находим:

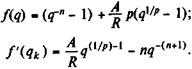
Начальныезначения оцениваемого показателя q выбирают так, чтобы a _n;i или 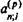были близки к заданному значению

Пример 4.15. Какова доходность инвестиций, выраженная в виде годовой процентной ставки, если вложения составили 100 млн. руб., ожидаемая отдача может быть представлена в виде квартальной постоянной ренты постнумерандо и годовая сумма дохода10 млн. руб.? Срок ренты 15 лет.

Величину инвестицийприравняем к современной стоимости ренты. Первоначальное значение процентной ставки найдем, отправляясь от заданного значения отношения A / R = 10. Этой величине долженбыть равен и коэффициент приведения Близкое значение коэффициента приходитсяна ставку 6%. Для этого уровня ставки = 9,93. Поскольку ставка несколько завышена, то возьмемв качестве исходнойменьшую величину, пусть это будет 5,9%. Тогда

f (l,059) = (1,059^-15 - 1) + 10 х 4(1,059^1/4 - 1) = 0,00059;

f '(l,059) = 10 х l,059^1/4-1 - 15 х 1,059^-16 = 3,5846;

q ₁ = 1,059 - 0,00059/3,5846 = 1,05883 или i =5,883%.

Проверка: 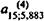= 10,0003. Таким образом, уже на первой итерации получено удовлетворительноеприближение.

Дата добавления: 2015-03-31