Решение. 1. Сначала пишем матрицу данной в условии модели:

1. Сначала пишем матрицу данной в условии модели:

(это немного кривая матрица)

2. Транспонируем ее, меняем строки со столбцами и получаем это:

-1 1 2

4 1 -1

-2 2 2

3. Из транспонированной матрицы составляем новую матемаическую модель, которая и будет двойственной к исходной. Перед тем,как переводить, надо обратить внимание на знаки, чтоб они все смотрели в одну сторону или было =. То есть либо так ≥, либо так ≤, либо так≥=, либо так≤=.

4. Так же мы переписываем целевую функцию. Меняем местами свободные члены исходной модели и коэффиценты в целевой функции. Так же исходая модель была на максимум, следовательно двойственная будет на минимум, следовательно знак будет такой в уравнениях ≥. Если же она была на минимум, а двойственная на максимум, то знак был бы вот такой ≤.

В свою очередь, поскольку Y3 – ЛЮБОЙ ЗНАК, то он будет у3=(у4-у5), следовательно целевая функция будет вот такая:

5. Теперь нам надо переписать модель с учетом изменений. Эту же модель мы позже будем заносить в EXEL.

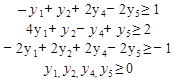
6. Переводим это в кaноническую форму.

Также мы добавляем в уравнения со знаком ≤ - одну дополнительную переменную со знаком – и искуственную переменную со знаком +, в последнем урвнении мы так же меняем знак. В итоге в каждом уравнении должно получится одна переменная с положительным знаком, когда все остальные будут равны 0.

Тут мы изменили последнюю строку, умножив на -1, поэтому искусственную перемнную с плюсом мы не добовляем, поскольку там появилась дополнительная переменная, которая больше нигде неповторяется.

7. Построим опорный план и окончательную целевую функцию.

Опорный план: У(0 0 0 0 0 0 1 1 2), это соответствует переменным (у1,у2,у4,у5,у6,у7,у8,у9,у10).

В целевой функции рядом с дополнительными переменными будут стоять 0, а рядом с искуственными М:

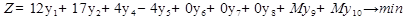
8. Строим первоначальную симплекс таблицу.

Базис	Св. чл.	У1	У2	У4	У5 -4	У6 (0)	У7 (0)	У8 (0)	У9 (M)	У10 (M)
У9(M)		-1			-2	-1
У10 (M)				-1			-1
У8(0)			-2	-2
Z	3M	3M-12	2M-17	3M-4	M+4	-M	-M

· В базис идут ИГРИКИ, которые повотряются только один раз в мат. Модели.

· Свободные члены (Св. Чл) – это то, чему равно выражение с данным иксом. Например, в выражение с У9 = 1, пишем 1.

· Чтоб полностью заполнить таблицу, берем коэффиценты у ИГРИКОВ и заполнем их в соответствующие клетки.

· Маленькие цифорки рядом с ИГРИКАМИ в таблице берутся из целевой функции, это их коэффиценты, на них надо будет умножать, чтоб найти Z для свободного члена, и вычитать – для обычных ИГРИКОВ..

· Чтоб найти Z: Y9*1+Y10*2+Y8*1 = 3M

· (-1*Y9+4*Y10+2*Y8) – 12 = 3M-12!; Далее продолжаем в том же духе.)(1*Y9+1*Y10-2*Y8) – 17 = 2M-17.

Теперь переходим к работе в EXEL.

Вводим целевую функцию, подписываем ячейки.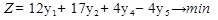

Вводим ограничения (уравнения) из мат модели,

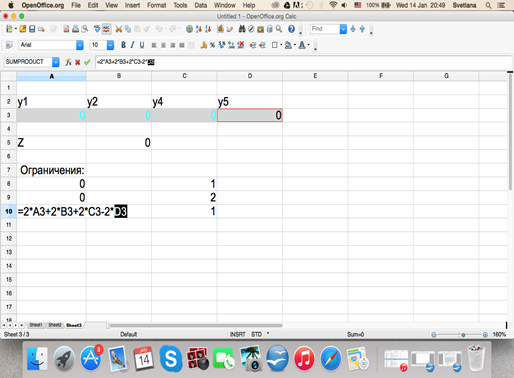
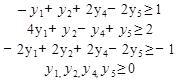
Далее используем поиск решений и получаем:

Поиск решений и ограничения.

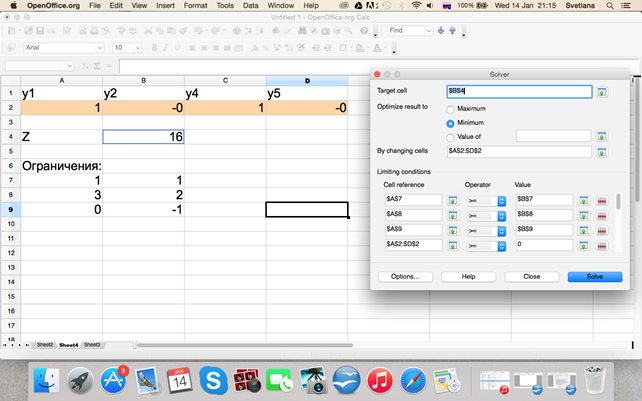
Надо не забыть посчитать обратно У3, в самом начале мы использовали формулу У3=(У4-У5), следовательно сейчас надо их сложить. Так как У4 = 1, а У5 = 0, то У3 будет = 1.

Экономическая интерпретация:

Найденный У является теневой ценой. Она показывает, на сколько увеличится исходная целевая функция, на сколько она изменится, при изменнеии ограничений на единицу. У2 = 0, это значит, что 2 ресурс нелимитирован и у него не существует остатка. У1 и У3 = 1, значит, чти товар дефицитный. Значение Целевой функции = 16.

Дата добавления: 2015-03-31