
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение двухфакторного уравнения регрессии
|
|
|
|
Сначала найдем среднеквадратическое отклонение ( ), (
), (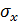 ) в ряду x и y, которое рассчитывается по формулам:
) в ряду x и y, которое рассчитывается по формулам:
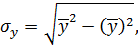 (2.1)
(2.1)
 . (2.2)
. (2.2)
где 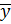 –– среднее значение результативного признака,
–– среднее значение результативного признака,
 –– среднее значение факторного признака.
–– среднее значение факторного признака.
С помощью формул (2.1) и (2.2) рассчитываем среднеквадратические отклонения в ряду y, x2 и x3.
 =
= 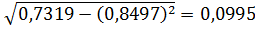
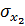 =
=  2
2

Прежде чем найти параметры уравнения множественной регрессии, определяют и анализируют парные коэффициенты корреляции ( ), (
), ( ) которые рассчитываются по формулам:
) которые рассчитываются по формулам:
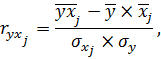

где 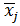 –– среднее значение j -го факторного признака;
–– среднее значение j -го факторного признака;
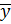 –– среднее значение результативного признака;
–– среднее значение результативного признака;
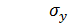 –– среднеквадратическое отклонение результативного признака;
–– среднеквадратическое отклонение результативного признака;
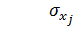 –– среднеквадратическое отклонение j -го факторного признака.
–– среднеквадратическое отклонение j -го факторного признака.
Парные коэффициенты корреляции равны:
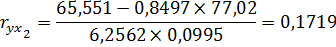

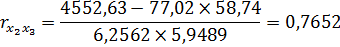
Связь между y и x2 прямая, слабая; связь между у и х3 обратная, очень слабая; связь между х2 и х3 прямая, тесная.
Наличие между двумя факторами х2 и х3 весьма тесной линейной связи (парный коэффициент корреляции 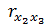 превышает по абсолютной величине 0,7) свидетельствует о наличии мультиколлениарности между факторами.
превышает по абсолютной величине 0,7) свидетельствует о наличии мультиколлениарности между факторами.
Чтобы найти параметры уравнения множественной регрессии и использовать при этом ранее найденные парные коэффициенты корреляции, строится система нормальных уравнений в стандартизированном масштабе.
Система нормальных уравнений в стандартизированном масштабе имеет следующий вид:
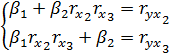 , (2.3)
, (2.3)
где 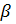 –– стандартизированный коэффициент регрессии.
–– стандартизированный коэффициент регрессии.
Подставляя в систему (2.3) ранее найденные парные коэффициенты корреляции получим:

Из системы (2.3) находим стандартизированные коэффициенты регрессии:
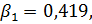
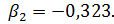
Коэффициент  по абсолютному значению больше коэффициента
по абсолютному значению больше коэффициента 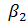 .
.
Фактор x2 влияет на результативный признак сильнее, чем фактор x3.
Уравнение регрессии в стандартизированном масштабе имеет следующий вид:
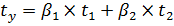 (2.4)
(2.4)
Подставив значения  и
и 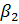 в уравнение (2.4) получим:
в уравнение (2.4) получим:
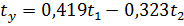
Переход от стандартизированного уравнения регрессии к уравнению регрессии в натуральном масштабе осуществляется по формулам:
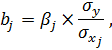
где 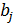 –– коэффициент регрессии при j-м факторном признаке,
–– коэффициент регрессии при j-м факторном признаке,
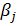 –– стандартизированный коэффициент регрессии при j-м факторном признаке.
–– стандартизированный коэффициент регрессии при j-м факторном признаке.

Найдем параметры искомого уравнения:

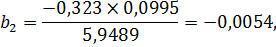
 .
.
Уравнение регрессии в натуральном масштабе находится по формуле:
 (2.5)
(2.5)
Подставив найденные параметры уравнения регрессии в уравнение (2.5) получим:
 .
.
С увеличением расходов на конечное потребление, в текущих ценах % к ВВП на 1% к ВВП, при исключении влияния второго фактора (расходы домашних хозяйств), индекс человеческого развития увеличиться на 0,0067, а при неизменном показателе расходов на конечное потребление, с увеличением расходов домашних хозяйств на 1% к ВВП индекс человеческого развития уменьшится на 0,0054.
Коэффициент множественной корреляции ( ) рассчитывается по формуле:
) рассчитывается по формуле:
 . (2.6)
. (2.6)
Подставив найденные ранее парные коэффициенты корреляции и стандартизированные коэффициенты регрессии в уравнение (2.6) получим:
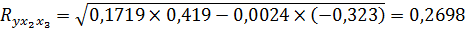 .
.
Величина коэффициента множественной корреляции отражает слабую связь факторов и результата.
Коэффициент множественной детерминации (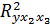 ) рассчитывается по формуле:
) рассчитывается по формуле:
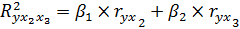 ,
,
 .
.
Доля факторной дисперсии в общей дисперсии составляет приблизительно 7%. На неучтённые факторы в модели приходится около 93%.
Средний коэффициент эластичности рассчитывается по формуле:

Для факторов х2 и х3 средние коэффициенты эластичности равны:

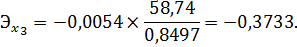
Общий коэффициент эластичности равен:

Эластичность по каждому фактору и в целом меньше единицы, следовательно, индекс человеческого развития увеличивается в меньшей степени, чем факторы. С увеличением расходов на конечное потребление на 1% от своего среднего уровня, индекс человеческого развития возрастает на 0,6073 % от своего среднего уровня, при увеличении расходов домашних хозяйств на 1 % от своего среднего уровня, индекс человеческого развития снижается на 0,3733 % от среднего уровня. Очевидно, что сила влияния расходов на конечное потребление на индекс человеческого развития больше, чем сила влияния расходов домашних хозяйств. С увеличением каждого фактора на 1% следует ожидать увеличения индекса человеческого развития на 0,234%.
F -критерий Фишера ( ) рассчитывается по формуле:
) рассчитывается по формуле:

где  –– коэффициент множественной детерминации;
–– коэффициент множественной детерминации;
n –– количество наблюдений;
m –– количество параметров в уравнении регрессии.

 равно 3,44 при уровне значимости:
равно 3,44 при уровне значимости:  равном 0,05 и степенях свободы:
равном 0,05 и степенях свободы:  равной 2 и
равной 2 и 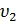 равной 22.
равной 22.  меньше
меньше 
Уравнение регрессии и показатель тесноты связи являются статистически незначимыми.
Частный F -критерий ( ) рассчитываются по формуле:
) рассчитываются по формуле:
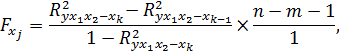
где 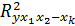 –– коэффициент множественной детерминации для модели с полным набором факторов;
–– коэффициент множественной детерминации для модели с полным набором факторов;
 –– тот же показатель, но без включения в модель фактора хk.
–– тот же показатель, но без включения в модель фактора хk.
Для факторов х2 и х3 частные F - критерии равны:
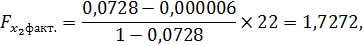

 равно 4,30 при уровне значимости
равно 4,30 при уровне значимости  равной 0,05 и степенях свободы:
равной 0,05 и степенях свободы:  равной 1 и
равной 1 и 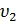 равной 22.
равной 22.
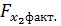 меньше
меньше  и
и 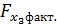 меньше
меньше 
Так как частные F -критерии меньше табличных, то гипотезу 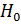 о несущественности прироста показателя множественной детерминации за счет включения фактора x2 и x3 принимаем. Низкое значение
о несущественности прироста показателя множественной детерминации за счет включения фактора x2 и x3 принимаем. Низкое значение  и
и 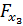 свидетельствует о статистической незначимости показателя детерминации, за счет включения в модель фактора
свидетельствует о статистической незначимости показателя детерминации, за счет включения в модель фактора 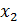 после фактора
после фактора  и фактора
и фактора  после фактора
после фактора 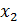 .
.
t -критерий Стьюдента ( ) рассчитывается по формуле:
) рассчитывается по формуле:
 (2.8)
(2.8)
Подставив найденные ранее частные F - критерии в формулу (2.8) получим:

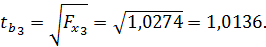
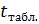 равно 2,0739 при уровне значимости
равно 2,0739 при уровне значимости  равном 0,05 и степени свободы
равном 0,05 и степени свободы  f равной 22.
f равной 22.
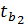 меньше
меньше 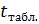 и
и  меньше
меньше 
Коэффициенты регрессии 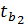 и
и  являются статистическими незначимыми.
являются статистическими незначимыми.
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 423; Нарушение авторских прав?; Мы поможем в написании вашей работы!