
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Клеммовые соединения
|
|
|
|
Краткие теоретические сведения
Испытание клеммовых соединений
Лабораторная работа 2.3
Проверка силы сдвига опытным путем
| Момент на ключе (Н·м) 0,25 Т зав÷ Т зав | ||||
| Сила трения при сдвиге F, Н (кН) | ||||
| Уточненный коэффициент трения в стыке | ƒс = |
Содержание отчета
1. Наименование работы.
2. Схема соединения для испытания.
3. Эскиз болтового соединения, вычерченный по размерам с натуры.
4. Расчет силы трения при сдвиге. Заполнить табл. 2.8.
5. Проверка силы трения опытным путем. Заполнить табл. 2.9.
6. Графики F - Т зав, расчетный и экспериментальный (рис. 2.7).
7. Выводы по работе.
Контрольные вопросы
1. Чем объяснить возможное несоответствие расчетной силы сдвига и определенной экспериментом силы сдвига для какого-либо момента завинчивания?
2. Какая наблюдается закономерность силы сдвига при изменении силы затяжки F 3 (момент завинчивания Т зав) и как это объяснить?
3. Какие изменения следует внести, чтобы при одной и той же затяжке увеличить силу сдвига?
4. Чем объяснить (если это имеет место) криволинейность графика зависимости F – Т зав?
5. Целесообразно ли использовать смазку при осуществлении этих соединений (если да, то где и с какой целью)?
Цель работы экспериментальное исследование зависимости осевого усилия, воспринимаемого клеммовым соединением, от усилия затяжки болта F 3.
Клеммовое соединение (рис 2.8) представляет собой разъемное соединение, основанное на действии сил трения, соединение, в котором между ступицей (для краткости клеммой) и валом необходимое нормальное давление создается затяжкой болтов (винтов, шпилек) [1, 2, 3].
|
Клеммовые соединения допускают постановку деталей в любом угловом положении, в любом положении по длине гладкого участка вала. Вал не ослабляется шпоночной канавкой, шлицами, как в шпоночном или шлицевом соединении.
На рис. 2.9 показаны клеммовые соединения с разъемной (рис. 2.9, а) и разрезной (рис. 2.9, б) ступицами.
Соединения с разъемной ступицей сложнее, их применяют при необходимости монтажа без снятия других деталей, расположенных на валу.
Клеммовые соединения нагружаются осевой силой Fa, крутящим моментом T, а также одновременно силой и моментом.
Если клеммовое соединение нагружается осевой силой Fa, то уравнение прочности, т.е. неподвижности ступицы относительно вала, запишется в виде

где Fa – осевая сила; 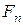 – суммарная, нормальная к поверхности вала сила со стороны полуступицы; f – коэффициент трения.
– суммарная, нормальная к поверхности вала сила со стороны полуступицы; f – коэффициент трения.
|
Если клеммовое соединение нагружается крутящим моментом Т, то уравнение прочности имеет вид
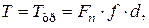 (1)
(1)
где d – диаметр вала.
При одновременном действии крутящего момента и осевой силы, сдвигающая сила определяется как равнодействующая окружной силы от момента  и осевой силы Fa
и осевой силы Fa
 ,
,
и уравнение прочности запишется по этой равнодействующей:
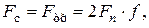 (1а)
(1а)
В данной работе проводится экспериментальное исследование зависимости осевой силы от силы затяжки 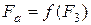 , т. е. при нагружении клеммового соединения осевой силой.
, т. е. при нагружении клеммового соединения осевой силой.
Величина  а следовательно, и закон распределения давления по окружности, зависит от характера соединения клеммы с валом при одном и том же усилии затяжки болта
а следовательно, и закон распределения давления по окружности, зависит от характера соединения клеммы с валом при одном и том же усилии затяжки болта 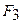 .
.
Для теоретических расчетов рассматриваются следующие три основных случая распределения давления (все случаи являются аппроксимацией фактического распределения давления).
1. Клемма обладает большой прочностью, а посадка деталей выполнена с большим зазором или же отверстие имеет эллиптическую форму (рис. 2.10). Наиболее наглядно это видно при разъемной ступице (рис. 2.10, а). При этом можно допустить, что контакт деталей происходит на небольшом участке, проектирующемся практически в точку. Тогда сила трения для полуступицы

где f – коэффициент трения.
Из условия равновесия полуступицы
FN 2 F 3
и тогда
 .
.
|
2. Давление распределяется по косинусоидальному (серповидному) закону (рис. 2.10, б). Такое распределение возможно при нежесткой ступице с первоначальным зазором или при жесткой ступице с малым натягом, что наиболее характерно при разрезной ступице. В этом случае давление на поверхности зажима повторяет эпюру вмятин вала в ступицу. Давление максимально в направлении, перпендикулярном к разъему, а сходит на нет в плоскости разъема по косинусоидальному закону р = р0 соsα (рис. 2.11).
Теоретическая зависимость между осевой силой и силой затяжки может быть получена при помощи следующего рассуждения.
|
Равнодействующая давления со стороны каждой полуступицы определится как сумма (интеграл) проекций элементарных сил на вертикальную ось z

 .
.
Суммарная нормальная к поверхности вала сила от каждой полуступицы определится как сумма элементарных сил

и, выражая р0 через F р, получим

Согласно равновесию полуступицы сила затяжки каждого из болтов при одном болте с каждой стороны
 или
или 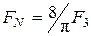 ,
,
а зависимость осевой силы и силы затяжки будет следующей
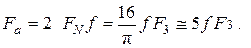 (3)
(3)
3. Равномерное распределение давления по окружности, приблизительно может иметь случай при сравнительно невысокой жесткости ступицы и момент от осевых сил затяжки болтов увеличивает давление вблизи разъема (рис. 2.10, в; рис. 2. 12).
|
Равнодействующая давления со стороны полуступицы

Суммарная, нормальная к поверхности вала сила от полуступицы

Согласно условию равновесия полуступицы, сила затяжки болта
 или
или 
Уравнение зависимости осевой силы и силы затяжки
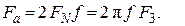 (4)
(4)
Итак, имеем три уравнения:
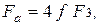
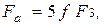

Полученные формулы пригодны как для клеммовых соединений с разъемной, так и с прорезной ступицей. При ступице с прорезью дополнительной затяжкой болтов для выборки зазоров обычно пренебрегают или, для большей надежности, вводится коэффициент 1,1.
Для вычисления максимального осевого усилия F, воспринимаемого клеммой, определяют допустимую силу затяжки
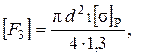 (5)
(5)
где d 1 - внутренний диаметр резьбы (см. табл.2.1 (лаб. раб. 2.1)ГОСТа на резьбу);[σ]р - допускаемое напряжение при растяжении
[σ]р = σт / S; (6)
σт - предел текучести материала болта (см. табл.2.2 (лаб. раб. 2.1); S - коэффициент запаса прочности: S = 2…3 (берется среднее значение 2,5).
Ступица проверяется на удельное давление:
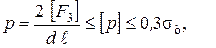 (7)
(7)
где σт - предел текучести материала ступицы.
Коэффициент трения ƒ в соединении зависит от материала (материалом является сталь по стали), от качества обработки поверхности (класс шероховатости) и удельного давления по поверхности ступицы. Класс шероховатости поверхности устанавливается по двум видам механической обработки – чистое течение и шлифование. Давление устанавливается расчетом по формуле (7).
График зависимости ƒ–р от обработки поверхности приводится на рис.2.13.

Рис. 2.13. Графики зависимости f–p: 1 – обработка: чистовое точение,
развертывание; 2 – обработка: шлифование
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 3701; Нарушение авторских прав?; Мы поможем в написании вашей работы!
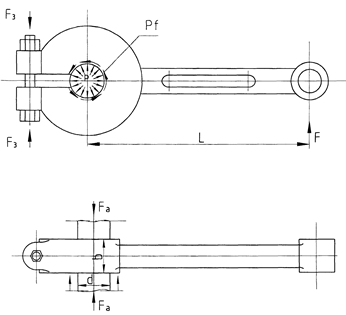 Рис.2.8. Нормальное давление в клеммовом соединении
Рис.2.8. Нормальное давление в клеммовом соединении
 а б
Рис. 2.9. Клеммовые соединения: а – с разрезной ступицей; б – с разъемной ступицей
а б
Рис. 2.9. Клеммовые соединения: а – с разрезной ступицей; б – с разъемной ступицей



 Рис. 2.11. Распределение давления по косинусоидальному закону
Рис. 2.11. Распределение давления по косинусоидальному закону
 Рис. 2.12. Равномерное распределение давление по окружности
Рис. 2.12. Равномерное распределение давление по окружности