Композиция автоматов

СХЕМЫ КОНЕЧНЫХ АВТОМАТОВ

Доказательство окончено.

Упражнение. Показать, что множество всех симметричных слов в алфавите { 0, 1 } не является автоматным.

Рассмотрим операции над автоматами, которые позволяют из одних автоматов образовывать другие автоматы. В частности, если задано фиксированное семейство простых автоматов, то из экземпляров автоматов семейства можно строить другие автоматы или даже любые возможные автоматы.

Для этого нам потребуется рассматривать входы и выходы автоматов как конечные системы входов и выходов.

То есть автомат может рассматриваться как устройство, имеющее несколько входов и несколько выходов, которые мы будем обозначать символами переменных x ₁,..., x_m и y ₁,..., y_n соответственно.

Тогда символами входного алфавита автомата Â, имеющего m входов, являются наборы длины m, компоненты которых одновременно поступают на входы Â.

Символы выходного алфавита Â, имеющего n выходов, - это наборы длины n, значения всех компонент которых одновременно появляются на выходах автомата Â в качестве результата его работы.

К основным операциям над автоматами относятся композиция и обратная связь.

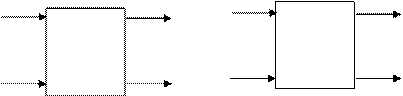
Пусть заданы автоматы Â ₁ и Â ₂, имеющие соответственно m ₁ и m ₂ входов, а также n ₁ и n ₂ выходов (рис. 7.11).

x ₁ y ₁ x ₁ y ₁

... Â ₁ ... Â ₂

x_{m 1} y_{n 1} x_{m 2} y_{n 2}

Рис. 7.11

Пусть k - такое целое число, что k 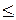n ₁ и k 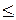m ₂.

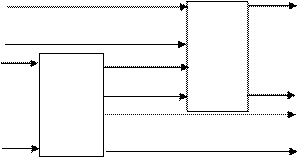
Тогда композицией Â ₁ и Â ₂ называется автомат, который получается из Â ₁ и Â ₂ подсоединением k различных выходов Â ₁ к k различным входам Â ₂.

Например, так как это выполнено для случая, изображенного на рис. 7.12.

... Â ₂

Дата добавления: 2015-03-31