При постоянном давлении

А б

II. ЦИКЛ С ПОДВОДОМ ТЕПЛОТЫ

ПРИ ПОСТОЯННОМ ОБЪЁМЕ

В 1862 г. французский инженер Бо де Роша предложил рабочий цикл ДВС с предварительным сжатием РТ и сгоранием при постоянном объёме. Исходя из этого в 1878 г. немецкий механик Н. Отто спроектировал и изготовил 4-х тактный двигатель, явившийся прообразом карбюраторных двигателей. В честь его и назван этот цикл – цикл Отто.

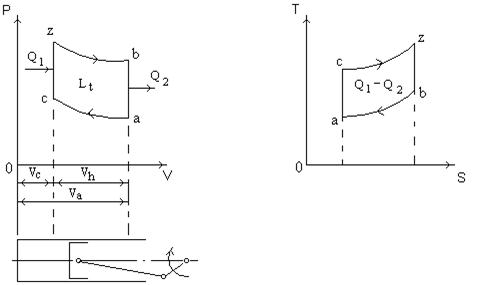
Рисунок 2.2 - Цикл Отто:

а – диаграмма в координатах р – v; б – в координатах T- S (тепловая диаграмма); Т – температура; S – энтропия, 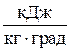; ас – адиабатное сжатие; сz – изохорный подвод тепла; zb – адиабатное расширение; bа – изохорный отвод тепла; V_h – рабочий объём; L_t – теоретическая работа, эквивалентная полезно использованной теплоте;

Основные параметры цикла:

ε – степень сжатия (см. рис. 2.2).

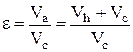, (2.3)

где: Va, Vc – соответственно полный и рабочий объёмы цилиндра;

Vh – объём камеры сгорания.

λ – степень нарастания давления. 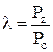. (2.4)

Тогда термический КПД будет равен (см. выражение 2.1)

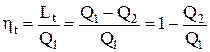. (2.5)

Использование теплоты в цикле удобно иллюстрировать с помощью тепловой диаграммы (рис.2.2б). Здесь площадь эквивалентна полному количеству теплоты.

Для изохорного процесса (при dV=0)

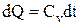
откуда 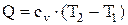(2.9)

Следовательно:

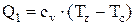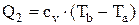; (2.10)

Подставляя в уравнение (2.5) значения Q₁ и Q₂ (см. выраж. 2.10), с учётом того что Сv = const, получаем

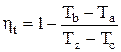. (2.18)

Выразим

Для адиабаты ас:

,

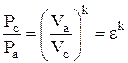откуда ; (2.6)

,

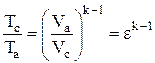откуда 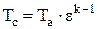, (2.7)

где k – коэффициент адиабаты. 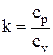; (2.8)

С_р – изобарная теплоёмкость (теплоёмкость при постоянном давлении).

С_v – изохорная теплоемкость. Это теплоёмкость РТ при постоянном объёме. В рассматриевом цикле рабочим телом является идеальный газ, имеющий постоянную теплоёмкость. С_v = const.

Тогда для изохоры сz:

,

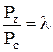откуда 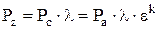; (2.11)

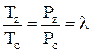
откуда 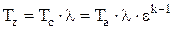(2.12)

Для адиабаты zв:

,

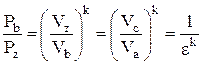откуда 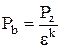. (2.13)

Подставляя значение 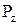(см. выраж. 2.12) получаем

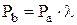; н (2.14)

,

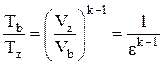откуда 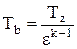. (2.15)

Подставляя значение T_z (см. выраж. 2.12) получаем

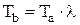. (2.16)

Подставляя значения в выражения 2.5 получаем:

.

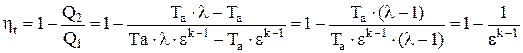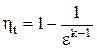. (2.17)

Из выражения 2.17 видно, что термический КПД зависит от степени сжатия и от коэффициента адиабаты.

Коэффициент адиабаты к характеризует физические свойства рабочего тела.

Для идеальных газов к = const = 1,4. Но для реального рабочего тела, даже с изменением кв узких пределах 1,2…1,4, h _t существенно зависит от этого параметра (рис. 2.3) [3].

По графику видно, что степень сжатия при её малых значениях существенно влияет на показатель h _{t ,} однако, при её дальнейшем увеличении, начиная примерно с e = 12 …14, это влияние уменьшается.

Полезная теоретическая работа цикла зависит от количества подведенного тепла и может быть выражена

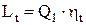(2.19)

Эта работа равна разности работ расширения и сжатия L_p и L_c. Она эквива- лентна полезно используемой теплоте Q₁ - Q₂ и представляет в системе координат

(рис. 2.2) площадь, ограниченный кривыми Lp и Lc, т. е. разность площадей, расположенными под кривыми Lp и Lc и осью абсцисс

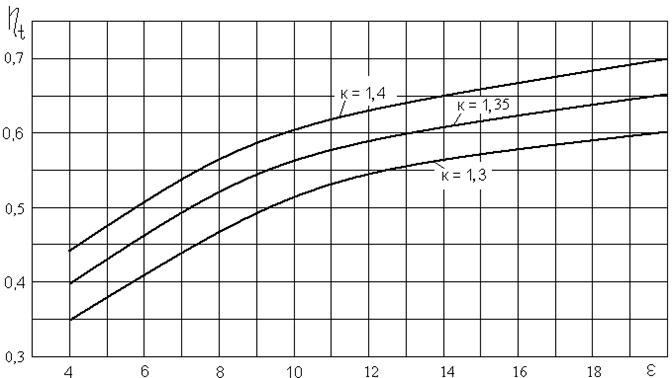
Рисунок 2.3 - Зависимость h _t от e и k

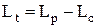(2.20)

Из курса технической термодинамики известно, что для адиабатных процессов расширения и сжатия

; .

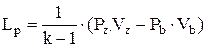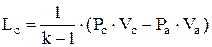Т. к. , , , , , ,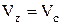

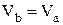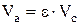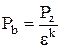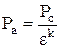Получим ,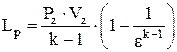

.

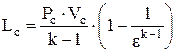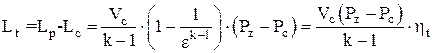. (2.21)

Из выражений 2.13—2.21 следует:

1. При увеличении e возрастает максимальное давление цикла P_z и дважды полезная термодинамическая работа L_t;

2. Уменьшаются температура Т_в и давление в конце такта расширения P_в, что приводит к уменьшению отводимой теплоты Q₂;

3. Из выражения (2.21) также видно, что полезная термодинамическая работа L_t зависит и от разности давлений P_z - P_c.

Из рис. 2.2.а видно, что чем больше разность давлений между линиями расширения и сжатия, тем больше площадь диаграммы, а значит и больше полезная теоретическая работа цикла.­­­­­­­­­­­­­­­

Введем понятие – «среднее цикловое давление P_t ».

Если площадь L_t (площадь четырёхугольника а-с-z-b) представить в виде прямоугольника с основанием V_h, лежащем на оси абсцисс ov, то линия, параллельная оси ov, и покажет среднее цикловое давление P_t

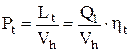. (2.22)

Выводы:

1. Среднее давление цикла P_t представляет собой удельную работу цикла (см. выраж. 2.2);

2. P_t существенно возрастает при увеличении степени сжатия только до определённых пределов (см. рис. 2.3);

3. Для существенного увеличения P_t, а значит и для увеличения полезной работы L_t, необходимо подводить большее количество теплоты, т.е. иметь топливо с более высокой теплотой сгорания.

III ЦИКЛ С ПОДВОДОМ ТЕПЛА

В 1893 г. немецкий инженер Р. Дизель теоретически разработал рабочий цикл двигателя с воспламенением от сжатия. Его именем и называется этот цикл – термодинамический цикл Дизеля.

Основные параметры данного цикла:

1) ε – степень сжатия, ;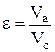

2) 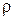– степень предварительного расширения, .

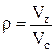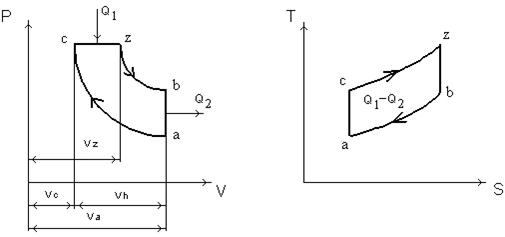
Рисунок 2.4 - Цикл дизеля

ас – адиабатное сжатие; сz – изобарный подвод теплоты; zb – адиабатное расширение; ba – изохорный отвод теплоты

Для определения термического КПД воспользуемся уравнением 1-го закона термодинамики

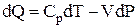(2.23)

При р=const 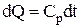; 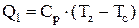(2.24)

По аналогии с методом анализа цикла Отто получаем

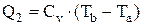(2.25)

Тогда термический КПД

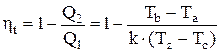. (2.26)

Выразим давления и температуры для цикла через исходные р_а и Т_а.

Для адиабаты ас (см. выраж. 2.6 и 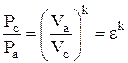2.7):

; ; (2.27)

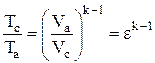, откуда 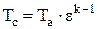. (2.28)

Для изобары cz:

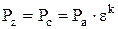; (2.29)

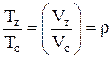, откуда 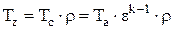(2.30)

Для адиабаты zb

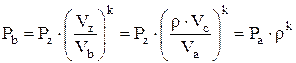, (2.31)

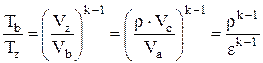, откуда

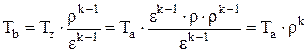. (2.32)

Подставляя полученные выражения в уравнение 2.25, получаем

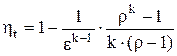. (2.33)

Из данной формулы видно:

А. Термический КПД η_t:

1. η_t повышается с увеличением степени сжатия e. Это объясняется возрастанием средней температуры подводимой теплоты. В цикле Дизеля высокие показатели степени сжатия не лимитируются детонацией, как в цикле Отто. Однако по мере роста e интенсивность увеличения η_t постепенно уменьшается (рис. 2.5а);

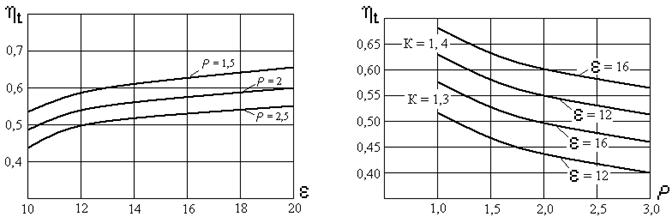
а б

Рисунок 2.5 - Зависимости: η_t от e и r при к = 1,35 (а);

η_t от r при различных e (б)

2. При любых значениях e термический КПД цикла Дизеля меньше термического КПД цикла Отто, т. к. множитель 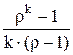всегда больше единицы (см. выраж. 2.17 и 2.28);

3. h_t зависит от степени предварительного расширения r,т. е. от нагрузки. Он уменьшается с увеличением r. Это объясняется тем, что с увеличением r растёт количество теплоты, отведённой холодному источнику, а значит и уменьшается количество теплоты, превращённой в механическую работу. При увеличении r возрастает количество подведенной по изобаре теплоты Q₁, что в реальных условиях соответствует повышению нагрузки. Следовательно, максимальное значение h_t достигается при минимальном количестве подведенной теплоты, что в реальных условиях имеет место при холостом ходе двигателя;

4. h_t зависит от показателя адиабаты k (рис. 2.5 б). Это объясняется увеличением потерь теплоты и снижением среднего циклового давления;

5. При малых значениях e и значительном подводе теплоты цикл Дизеля вообще не существует, т. к. r не может превышать e;

6. Использование этого цикла в качестве прототипа рабочих процессов в реальных двигателях целесообразно только при значительных e (более 10), при работе с неполной нагрузкой (меньше r) и при значительно обеднённой смеси (приближение к к значению к воздушного цикла).

Всё, выше сказанное, свидетельствует о том, что данный цикл не используется в качестве прототипа для организации рабочего цикла в современных автомобильных двигателях.

Дата добавления: 2015-03-31