
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Арктангес числа
|
|
|
|
Арксинус числа
Арккосинус числа
Функция косинуса убывает на отрезке [0; π] и принимает значения от -1 до 1. Следовательно, по теореме о корне для любого числа a, такого, что |a|≤1, в промежутке [0; π] существует единственный корень b уравнения cos(x)=a. Это число b называют арккосинусом числа a и обозначают arccos(a) (см. рисунок ниже).

Определение: Арккосинусом числа a называется такое число из отрезка [0; π], косинус которого равен a.
№18
Функция синуса возрастает на отрезке [-π/2; π/2] и принимает значения от -1 до 1. Следовательно, по теореме о корне для любого числа a, такого, что |a|≤1, в промежутке [-π/2; π/2] существует единственный корень b уравнения sin(x)=a. Это число b называют арксинусом числа a и обозначают arcsin(a) (см. рисунок ниже).
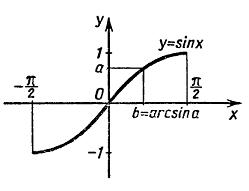
Определение: Арксинусом числа a называется такое число из отрезка [-π/2; π/2], синус которого равен a.
№19
Функция тангенса возрастает на интервале (-π/2; π/2) и принимает все значения из поля действительных чисел. Следовательно, по теореме о корне для любого числа a на интервале (-π/2; π/2) существует единственный корень b уравнения tg(x)=a. Это число b называют арктангенсом числа a и обозначают arctg(a) (см. рисунок ниже).

Определение. Арктангенсом числа a называется такое число из интервала (-π/2; π/2), тангенс которого равен a.
№20
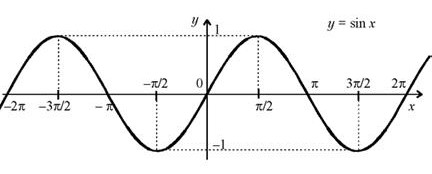
Функция y=sinx ее свойства и график
а) Область определения: D (sin x) = R.
б) Множество значений: E (sin x) = [ – 1, 1 ].
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T = 2  .
.
д) Нули функции: sin x = 0 при x =  n, n
n, n 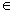 Z.
Z.
е) Промежутки знакопостоянства:
 ;
; 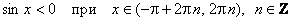 .
.
ж) Промежутки монотонности:
 ;
;
 .
.
з) Экстремумы:
 ;
; 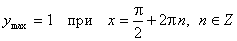 .
.
График функции y = sin x изображен на рисунке.
№21
а) Область определения: D (cos x) = R.
б) Множество значений: E (cos x) = [ – 1, 1 ].
в) Четность, нечетность: функция четная.
г ) Периодичность: функция периодическая с основным периодом T = 2  .
.
д) Нули функции: cos x = 0 при x =  +
+  n, n
n, n 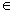 Z.
Z.
е) Промежутки знакопостоянства:
 ;
;
 .
.
. ж) Промежутки монотонности:
 ;
;
 .
.
з) Экстремумы:
 ;
;  .
.
График функции y = cos x изображен на рисунке.
№22
а) Область определения: D (tg x) = R \ {  /2 +
/2 +  n (n
n (n  Z) }.
Z) }.
б) Множество значений: E (tg x) = R.
в) Четность, нечетность: функция нечетная.
г ) Периодичность: функция периодическая с основным периодом T =  .
.
д) Нули функции: tg x = 0 при x =  n, n
n, n 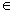 Z.
Z.
е) Промежутки знакопостоянства:
 ;
; 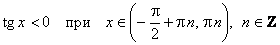 .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
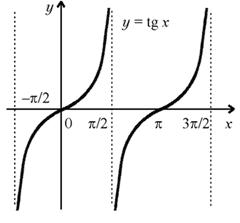
График функции y = tg x изображен на рисунке.
№23
Производная, её геометрический и механический смысл
Важнейшим понятием математического анализа является производная, которая определяет скорость изменения функции.
* Производной функции f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента, при стремлении последнего к нулю
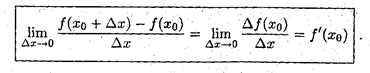
| Производная степенной функции |
Если f(x) = xp, где p - действительное число, то
 Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то
Если показатель степени является отрицательным числом, т.е. f(x) = x−p, то
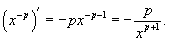 №24
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
№24
Геометрический смысл производной. Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
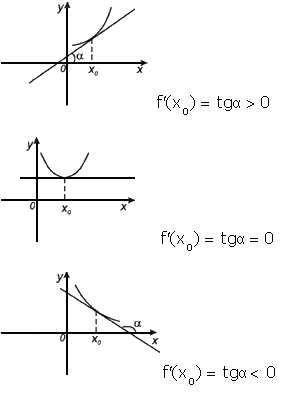 Рассмотрим график функции y = f (x):
Рассмотрим график функции y = f (x):
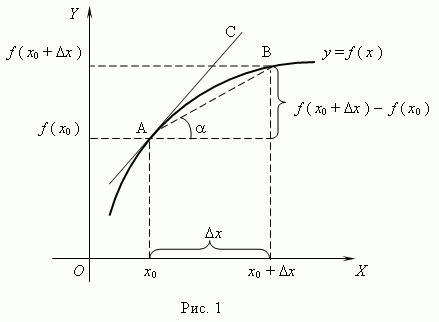 Из рис.1 видно, что для любых двух точек A и B графика функции:
Из рис.1 видно, что для любых двух точек A и B графика функции:  xf (x 0+ xf (x 0+  x)− f (x 0)= tg x)− f (x 0)= tg  , где , где  - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
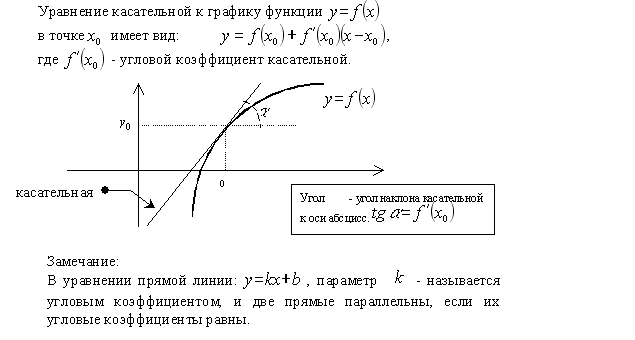
Уравнение касательной
Производной функции f (x) в точке x 0 называется предел отношения приращения функции в этой точке x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.
Уравнение касательной
Производной функции f (x) в точке x 0 называется предел отношения приращения функции в этой точке  f = f (x 0+ f = f (x 0+  x)− f (x 0) к приращению аргумента x)− f (x 0) к приращению аргумента  x при x при  x x  0: f 0: f  (x 0)= lim (x 0)= lim  x x  0 0  xf (x 0+ xf (x 0+  x)− f (x 0).
Геометрический смысл производной
Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке. x)− f (x 0).
Геометрический смысл производной
Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.
 №25
Правила дифференцирования
Если функции f и g дифференцируемы в точке x 0 то в этой же точке дифференцируемы сумма, произведение и частное (если g
№25
Правила дифференцирования
Если функции f и g дифференцируемы в точке x 0 то в этой же точке дифференцируемы сумма, произведение и частное (если g  (x 0) (x 0)  =0) этих функций, причем =0) этих функций, причем
 =0.
· Если функции u и v дифференцируемы в точке x, то (v + u) =0.
· Если функции u и v дифференцируемы в точке x, то (v + u)  = v = v  + u + u  .
· Если функция Cu, где C - постоянная, дифференцируема в точке x, то (С u) .
· Если функция Cu, где C - постоянная, дифференцируема в точке x, то (С u)  =С u =С u  .
· Если функции u и v дифференцируемы в точке x, то (u .
· Если функции u и v дифференцируемы в точке x, то (u  v) v)  = u = u   v + u v + u  v v  .
· Если функции u и v дифференцируемы в точке x и v (x) .
· Если функции u и v дифференцируемы в точке x и v (x)  =0, то (vu) =0, то (vu)  = v 2 u = v 2 u   v − u v − u  v v  .
Дифференцирование сложной функции.
Рассмотрим функцию y = sin x2. Чтобы найти значение этой функции в фиксированнной точке x нужно: 1) вычислить x2; 2) найти значение синуса от полученного значения x2. Иными словами, сначала надо найти значение g (x) = x2, а потом найти sin g (x). В подобных случаях говорят, что задана сложная функция y = f (g (x)). В нашем примере u = g (x) = x2, а y = f (u) = sin u.
Пусть y = f (g (x)) - сложная функция, причем функция u = g (x) дифференцируема в точке x, а функция y = f (u) дифференцируема в соответствующей точке u. Тогда функция y = f (g (x)) дифференцируема в точке x, причем y .
Дифференцирование сложной функции.
Рассмотрим функцию y = sin x2. Чтобы найти значение этой функции в фиксированнной точке x нужно: 1) вычислить x2; 2) найти значение синуса от полученного значения x2. Иными словами, сначала надо найти значение g (x) = x2, а потом найти sin g (x). В подобных случаях говорят, что задана сложная функция y = f (g (x)). В нашем примере u = g (x) = x2, а y = f (u) = sin u.
Пусть y = f (g (x)) - сложная функция, причем функция u = g (x) дифференцируема в точке x, а функция y = f (u) дифференцируема в соответствующей точке u. Тогда функция y = f (g (x)) дифференцируема в точке x, причем y  = f = f  (g (x)) (g (x))  g g  (x). Запись f '(g (x)) означает, что производная вычисляется по формуле для f '(x), но вместо x подставляется g (x). (x). Запись f '(g (x)) означает, что производная вычисляется по формуле для f '(x), но вместо x подставляется g (x).
 Функция y=tgx
1) y= tg x, x
Функция y=tgx
1) y= tg x, x   /2, k e z
y/=(tg x)/=(sin x)/(cos x)= ((sin x)/cos x- sin x(cos x)/)/cos2x= 1/cos2x;=>(tg x)/=1/cos2x /2, k e z
y/=(tg x)/=(sin x)/(cos x)= ((sin x)/cos x- sin x(cos x)/)/cos2x= 1/cos2x;=>(tg x)/=1/cos2x
|
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 1582; Нарушение авторских прав?; Мы поможем в написании вашей работы!
 N также дифференцируема, причем (fn)
N также дифференцируема, причем (fn)  (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем
(y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем