Примеры тел вращения

§ Шар — образован полукругом, вращающимся вокруг диаметра разреза

§ Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон

За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.

§ Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов

За площадь боковой поверхности конуса принимается площадь ее развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)

§ Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его ^[1]

При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

13. Конус.

Ко́нус (от др.-греч. κώνος «шишка») — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Также можно сказать, что это тело, полученное при вращении прямоугольного треугольника вокруг одного из его катетов. Далее будет рассматриваться именно этот случай, если не оговорено обратное. Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

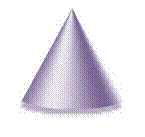
14. Усеченный конус.
Усеченный конус – часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

15. Шар и сфера. Взаимное расположение плоскости и шара.

Сфера — это множество точек в пространстве, равноудаленных от фиксированной точки (центра сферы).

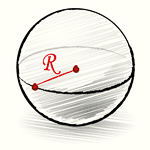
Шар — это тело, ограниченное сферой (рис.); его можно рассматривать как результат вращения круга вокруг его диаметра.

Шар или сфера. Шаровой, или сферической поверхностью (иногда просто сферой) называется геометрическое место точек пространства, равноудаленных от одной точки - центра шара. Площадь поверхности сферы равна учетверенной площади большого круга:

S = 4π R ^2

16. Понятие объема. Объем параллелепипеда.

Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жордан (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.

Объём параллелепипеда V=abc, где a, b, c — измерения прямоугольного параллелепипеда.

17. Объем призмы.

Объем призмы ранен V = S_основ • H. где S_основ — площадь основания призмы. H — ее высота.

Исходим из известного факта: объем параллелепипеда, равен

V_пар = S_основ • H

(S_основ - площадь основания, H — высота).

Начнем с частного случая. Пусть нам дана треугольная призма.

Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому

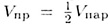
С другой стороны,

а высота призмы и параллелепипеда общая. Из равенства

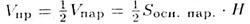
следует, что

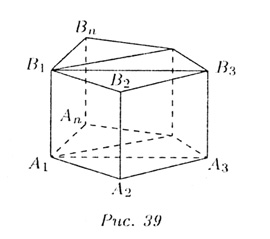
Переходим теперь к общему случаю. Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен

V_k = S_k • H

где S_k — площадь ее основания, H — высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:

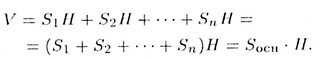
18. Объем пирамиды и усеченной пирамиды.

Дата добавления: 2015-04-23