Характеристика КИО-фильтров

Синтез КИО-фильтров

6.Применить оконную функцию к импульсной характеристике.

Окном называют некоторую четную функцию, определенную на интервале

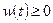Равную нулю за пределами этого интервала и обладающую следующими свойствами:

1.Структурная устойчивость.

2.Отсутствие накапливаемой ошибки.

3. Наличие прототипа в области непрерывных сигналов (линии задержки.

4.Линейная фазо-частотная характеристика (ФЧХ).

5.Простота выбора коэффициентов и лёгкость проектирования.

6.Доступность средств автоматизированного проектирования (САПР).

7.КИО-фильтры принципиально вносят запаздывание.

8.Высокоэффективные КИО-фильтры строятся с большим числом операций умножения с накоплением и поэтому их реализация требует значительных вычислительных затрат.

9.При одной и той же амплитудно-частотной характеристике (АЧХ) БИО-фильтры имеют меньший порядок, чем КИО-фильтры, т.е. Обеспечивают более высокое быстродействие, меньшее запаздывание и более простую реализацию.

21. Структура БИО-фильтров. Каскадная форма.

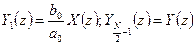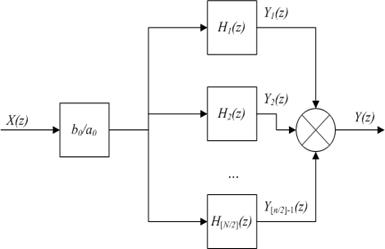
Параллельная форма

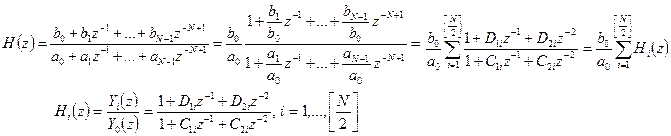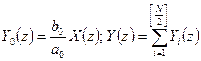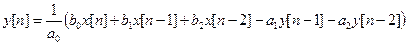Прямая форма I.

Прямая форма II.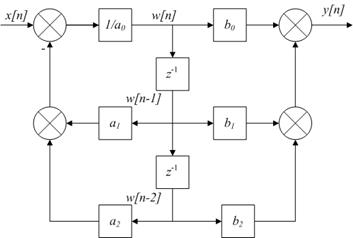

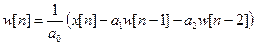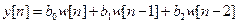22. Характеристика БИХ-фильтров

Определим характерные черты КИХ-фильтров, которые определяются природой БИХ-фильтров как фильтров с обратной связью или рекурсивных фильтров.

1. Простая структура. БИХ-фильтры могут быть реализованы с более простой структурой, меньшим количеством вычислений и объемом памяти, чем КИХ-фильтры, при тех же требованиях по качеству и обеспечении устойчивости. Это связано с тем, что БИХ-фильтры реализуются при помощи нулей и полюсов передаточной функции, тогда как КИХ-фильтры реализуются только через нули.

2. Реализация с использованием каскадного соединения секций второго порядка. БИХ-фильтры высокого порядка, созданные непосредственно по уравнениям (2.2) или (2.12)–(2.13), накапливают ошибки квантования (из-за арифметики с фиксированной точкой и конечной длины слова), что может вызывать неустойчивость работы фильтра и большие ошибки. По этой причине правильнее расположить каскадно несколько биквадратных звеньев с соответствующими коэффициентами. Данные при вычислении биквадратных фильтров могут масштабироваться раздельно, а затем биквадратные звенья каскадируются для минимизации ошибок квантования коэффициентов и ошибок рекурсивного накопления. Каскадные биквадратные фильтры работают более медленно, чем их эквиваленты прямой формы реализации, но они более устойчивы и в них минимизируются эффекты, связанные с арифметическими ошибками конечной разрядности данных. Анализ БИХ-фильтров сводится к анализу секций 2-го порядка.

3. Аналоговые прототипы. БИХ-фильтры имеют традиционные аналоговые эквиваленты (фильтры Баттерворта, Чебышева, эллиптический и Бесселя) и могут быть проанализированы и синтезированы с использованием традиционных методов проектирования фильтров.

4. Доступность средств автоматизированного проектирования (САПР), такие как Matlab, labview и др.

5. Наличие проблем с устойчивостью.

6. Нелинейность ФЧХ. БИХ-фильтр имеет нелинейную ФЧХ, что неприемлемо в некоторых приложениях.

7. Наличие накапливаемой ошибки на выходе БИХ-фильтра при нуле на входе.

23. Сравнительная характеристика прототипов.

Характе- ристика   Прототип	Пульсации АЧХ в полосе пропускания	Пульсации АЧХ в полосе подавления	Характер ФЧХ	Ширина полосы перехода
Эллиптиче-ский (Кауэра)	+	+	Нелинейность уменьшается	Увеличивается при Одном и том же порядке
Чебышева 2 рода (Инверсный Чебышев)	–	+
Чебышева 1 рода	+	–
Баттерворта	–	–
Бесселя (Томпсона)	–	–	Линейная

24.

25. Устойчивость

Об устойчивости фильтра с бесконечной импульсной характеристикой судят по его передаточной функции. Для дискретного фильтра необходимо и достаточно, чтобы все полюса его передаточной функции по модулю были меньше единицы (т.е. Лежали внутри единичного круга на z-плоскости). Все критерии устойчивости, применимые в теории линейных стационарных систем, например критерий устойчивости Найквиста или критерий устойчивости Рауса применимы и в случае БИХ-фильтров.

В отличие от БИХ-фильтров, КИХ-фильтры всегда являются устойчивыми.

26. Популярный метод проектирования БИХ-фильтра сводится к тому, что сначала проектируется эквивалентный аналоговый фильтр, а затем функция передачи H(s) преобразуется математически в z - область, H(z) (рис. 2.6) с использованием комплексных отображений.

27. Билинейная трансформация – это отображение один к одному, которое исключает проблему помех от дискретизации путем перевода аналоговой частотной характеристики в передаточную функцию цифровой системы с соответствующим частотным откликом, это переход от производных в дифференциальных уравнениях к конечным разностям.

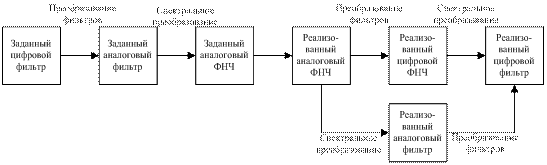
Билинейная трансформация определяется отображением 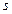на :

,

где Т – это период дискретизации. Обратное преобразование:

.

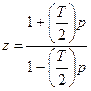28.

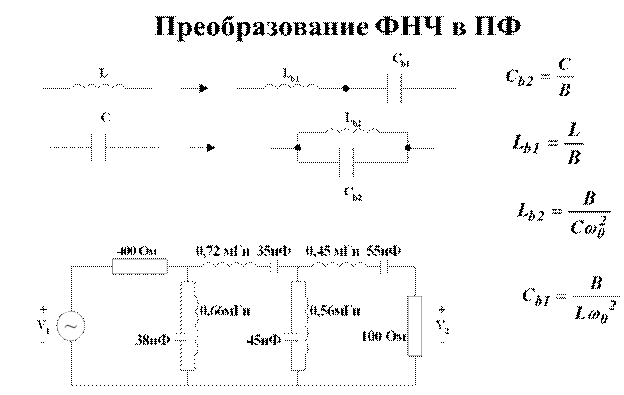
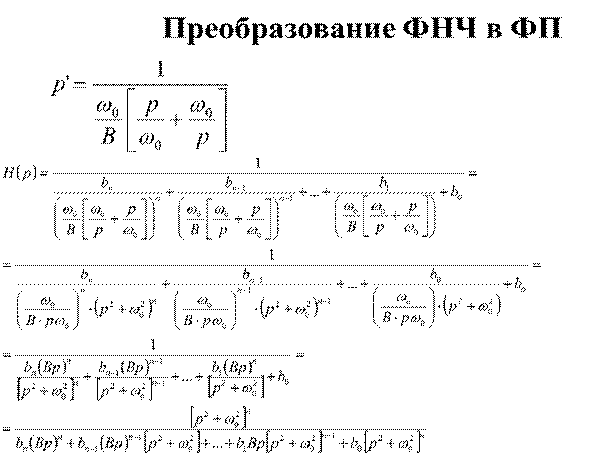
29.

Рис. 2.9. Увеличение крутизны перехода от полосы пропускания к полосе подавления

1.

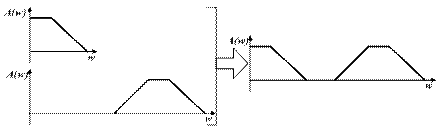
Рис. 2.10. Фильтр-пробка, спроектированный посредством параллельного соединения ФНЧ и ФВЧ

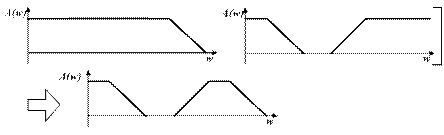
Рис. 2.11. Фильтр-пробка, спроектированный посредством каскадного соединения ФНЧ и ПФ.

Дата добавления: 2015-04-23