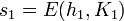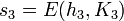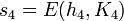КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие коллизии и причины ее существования. Парадокс дней рождения. Длина кода аутентификации сообщения (имитовставки)
|
|
|
|
Задача нахождения дискретного логарифма в конечном поле и криптографическая система ElGamal. Общая схема и пример шифрования и дешифрования. Достоинства и недостатки. Стойкость к атаке полным перебором.
Задача факторизации больших чисел и криптографическая система RSA. Общая схема и пример шифрования и дешифрования. Достоинства и недостатки. Рекомендации о длине ключа RSA Labs и NIST. Стойкость к атаке полным перебором.
Задача факторизации больших чисел – это задача разложения числа N на произведение простых чисел. Это NP задача.
RSA использует эту задачу для построения однонаправленной функции с секретом.
RSA-ключи генерируются следующим образом:
1. Выбираются два различных случайных простых числа 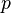 и
и  заданного размера (например, 1024 бита каждое).
заданного размера (например, 1024 бита каждое).
- Вычисляется их произведение
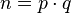 , которое называется модулем.
, которое называется модулем. - Вычисляется значение функции Эйлера от числа
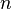 :
:

- Выбирается целое число
 (
( ), взаимно простое со значением функции
), взаимно простое со значением функции 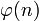 . Обычно в качестве
. Обычно в качестве  берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537. - Число
 называется открытой экспонентой
называется открытой экспонентой - Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в
 .
. - Слишком малые значения
 , например 3, потенциально могут ослабить безопасность схемы RSA.
, например 3, потенциально могут ослабить безопасность схемы RSA. - Вычисляется число
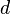 , мультипликативно обратное к числу
, мультипликативно обратное к числу  по модулю
по модулю 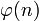 , то есть число, удовлетворяющее условию:
, то есть число, удовлетворяющее условию: -

- Число
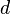 называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида. - Пара
 публикуется в качестве открытого ключа RSA.
публикуется в качестве открытого ключа RSA. - Пара
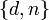 играет роль закрытого ключа RSA и держится в секрете.
играет роль закрытого ключа RSA и держится в секрете.
Общая схема работы:
 Шифрование:
Шифрование: 
Расшифрование: 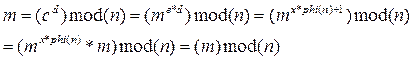
Пример: p=7, q=13, m=10
n=7*13=91; 
e=17;
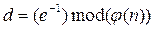
Расширенный алгоритм Эвлида:
| a | b | c | d | x1 | x2 | y1 | y2 |
| -4 | |||||||
| -4 | -4 |
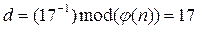
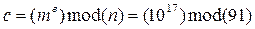

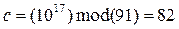
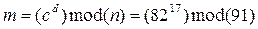
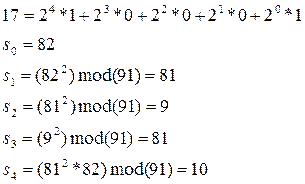
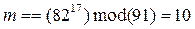
Задача нахождения дискретного логарифма в конечном поле: любой элемент поля есть некая степень примитивного элемента этого поля. Нахождения показателя степени по элементу (дискретного логарифма) – NP задача.
Схема Эль-Гамаля (Elgamal) — криптосистема с открытым ключом, основанная на трудности вычисления дискретных логарифмов в конечном поле. Криптосистема включает в себя алгоритм шифрования и алгоритм цифровой подписи.
Генерация ключа:
- Генерируется случайное простое число
 длины
длины  битов.
битов. - Выбирается случайный примитивный элемент
 поля
поля  .
. - Выбирается случайное целое число
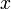 такое, что
такое, что  .
. - Вычисляется
 .
. - Открытым ключом является тройка
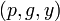 , закрытым ключом — число
, закрытым ключом — число 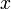 .
.
Общая схема:
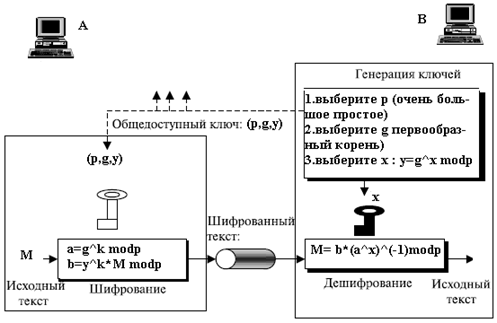
Шифрование:
Сообщение 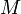 шифруется следующим образом:
шифруется следующим образом:
Выбирается сессионный ключ — случайное целое число  такое, что
такое, что 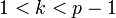
Вычисляются числа  и
и  .
.
Пара чисел  является шифротекстом.
является шифротекстом.
Нетрудно видеть, что длина шифротекста в схеме Эль-Гамаля длиннее исходного сообщения  вдвое.
вдвое.
Расшифрование
Зная закрытый ключ 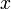 , исходное сообщение можно вычислить из шифротекста
, исходное сообщение можно вычислить из шифротекста  по формуле:
по формуле:
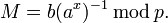
При этом нетрудно проверить, что

и поэтому
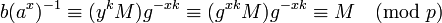 .
.
Для практических вычислений больше подходит следующая формула:

Пример: p=11, g=2. M=9, x=4,k=8
Шифрование:
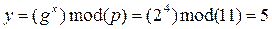

Шифротекст: (3,3)
Расшифрование
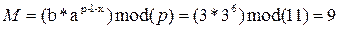
37. Целостность. Избыточность как способ обеспечения целостности данных. Классификация методов. Код аутентификации сообщения (имитовставка). Функция хеширования и ее свойства. Сжимающая функция (структура Merkle–Damgard).
Задача обеспечения целостности – заключается в необходимости удостовериться, не были ли внесены изменения в исходные данные, не зная их заранее. Если избыточность данных равна 0, то обеспечить их целостность невозможно. Поэтому для решения задача целостности избыточность вносится в данные специально.
Процесс контроля целостности обеспечивается введением в передаваемую информацию избыточности. Это достигается добавлением к сообщению некоторой проверочной комбинации. Такая комбинация вычисляется согласно определенным алгоритмам и играет роль индикатора, с помощью которого проверяется целостность сообщения. Именно этот момент дает возможность проверить, были ли изменены данные третьей стороной. Дополнительную избыточную информацию, вносимую в сообщение, называют имитовставкой.
m – исходное сообщение
h = f(m) – контрольная последовательность исходного сообщения
m’ – принятое сообщение
h’ = g(m’) – контрольная последовательность принятого сообщения
Если h=h’, то с большой вероятностью и m=m’
Методы:
-
 – симметричные
– симметричные -
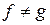 – ассиметричные
– ассиметричные
h – также называется хэш значением, имитовставкой или кодом аутентификации сообщения(MAC)
Свойства хэш функции y=f(x):
1. Незначительное изменение x должно вести к значительному изменению y.
2. Множество значений у < множества значений x, поэтому для x может существовать x’, для которого f(x)= f(x’). Поиск x’ по x должен быть NP задачей Для исключения атаки полным перебором длина х>64 бит
3. f(x) – однонаправленная функция. Обратное преобразование должно быть NP задачей
4. Сама f(x) – P задача и должна вычисляться быстро.
Для выполнения пункта 3 можно использовать сжимающую функцию с потерей, в этом случае речь идет о хэш функции, построенной по структуре Merkle–Damgard:
Структура Меркла-Дамгарда — метод построения криптографических хеш-функций. Криптографическая хеш-функция должна преобразовывать входное сообщение произвольной длины в выходное сообщение фиксированной длины. Этого можно достичь путём разбиения входного сообщение на блоки одинакового размера и их последовательной обработки односторонней функцией сжатия, которая преобразовывает входное сообщение фиксированной длины в более короткое выходное сообщение фиксированной длины. Функция сжатия либо может быть специально построена для хеширования либо может представлять собой функцию блочного шифрования. Хеш-функция Меркла-Дамгарда разбивает входное сообщение на блоки и работает с ними по очереди с помощью функции сжатия, каждый раз принимая входной блок с выходным от предыдущего раунда.
Коллизия – это ситуация, когда разные блоки исходного текста имеют одинаковый хэш.
(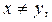 но
но  ).
).
Причина существования коллизий очевидна – хэш функция отображает большое множество исходных текстов на меньшее множество хэшей – следовательно поскольку хэшей меньше, чем сообщений, но каждому сообщению соответствует хэш, то один или более хэшей соответствуют сразу нескольким сообщениям. Единственный способ избавиться от коллизий совсем – взять мощность множества хэшей не меньше, чем мощность множества сообщений.
Парадо́кс дней рожде́ния — это кажущееся парадоксальным утверждение, что вероятность совпадения дней рождения (числа и месяца) хотя бы у двух членов группы из 23 и более человек, превышает 50 %. С практической точки зрения это означает, что если, например, в вашем классе более 22 учеников, то более вероятно, что у кого-то из одноклассников дни рождения придутся на один день, чем что у каждого будет свой собственный день рождения.
Аналогично число значений которые нужно перебрать, чтобы с высокой вероятностью найти коллизию значительно меньше, чем мощность пространства значений хэш функции. Это приводит к необходимости значительно большей длины имитовставки, чем кажется на первый взгляд (512 бит уже недостаточно), для того, чтобы поиск коллизий стал бы по-настоящему вычислительно невыполнимой задачей.
39. Алгоритм хеширования MD5: параметры, алгоритм забивки, алгоритм изменения переменных сцепления, раунды и операции, функции раундов. Стойкость к поиску коллизий.
Параметры:
- Длина хэша: 128 бит.
- Количество раундов: 4(по 16 проходов каждый).
- Длина хэшируемого сообщения: произвольная (L).
- Размер блока хэшируемого сообщения: 512 бит
Алгоритм забивки:
- Сначала дописывают единичный бит в конец потока (байт 0x80), затем необходимое число нулевых бит. Входные данные выравниваются так, чтобы их новый размер
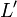 был сравним с 448 по модулю 512 (
был сравним с 448 по модулю 512 (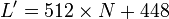 ). Выравнивание происходит, даже если длина уже сравнима с 448.
). Выравнивание происходит, даже если длина уже сравнима с 448.
- В оставшиеся 64 бита дописывают 64-битное представление длины данных (количество бит в сообщении) до выравнивания. Сначала записывают младшие 4 байта. Если длина превосходит
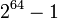 , то дописывают только младшие биты. После этого длина потока станет кратной 512. Вычисления будут основываться на представлении этого потока данных в виде массива слов по 512 бит.
, то дописывают только младшие биты. После этого длина потока станет кратной 512. Вычисления будут основываться на представлении этого потока данных в виде массива слов по 512 бит.
Алгоритм изменения переменных сцепления:
- Начальное значение переменных задается, как
А = 01 23 45 67;
В = 89 AB CD EF;
С = FE DC BA 98;
D = 76 54 32 10.
- Задается таблица констант
 — 64-элементная таблица данных, построенная следующим образом
— 64-элементная таблица данных, построенная следующим образом 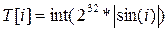
- Выровненные данные разбиваются на блоки по 512 бит, которые в свою очередь делятся на слова по 32 бита (16 штук). Каждый блок проходит через 4 раунда по 16 операторов в каждом Результаты A,B,C,D для каждого блока суммируются. При этом сумма с предыдущего этапа обрабатывается новым этапом(т. е. начальные значения задаются только для первого блока. Перед каждым последующим содержимое регистров запоминается, дальше оно же обрабатывается со следующим блоком и потом к результату обработки добавляется запомненное.)
- Всего операторов 64. На каждом операторе(см. схему ниже) выбирается T[i], где i – номер оператора от 1 до 64.
- Xk – одно из 16 32-битовых слов текущего блока. На каждом раунде обрабатываются все 16 слов(по одному на оператор) в разном порядке.
- s принимает одно из 4 значений циклически каждый оператор в одном раунде. У разных раундов разных четверки значений s
- Функция F определяется номером раунда
Схема оператора:

Ф-ции раундов:
1 раунд 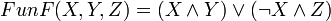 .
.
2 раунд  .
.
3 раунд 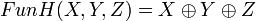 .
.
4 раунд 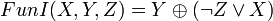 .
.
Коллизии MD5
В 2004 году китайские исследователи Ван Сяоюнь (Wang Xiaoyun), Фэн Дэнго (Feng Dengguo), Лай Сюэцзя (Lai Xuejia) и Юй Хунбо (Yu Hongbo) объявили об обнаруженной ими уязвимости в алгоритме, позволяющей за небольшое время (1 час на кластере IBM p690) находить коллизии.
В 2005 году Ван Сяоюнь и Юй Хунбо из университета Шаньдуна в Китае опубликовали алгоритм, который может найти две различные последовательности в 128 байт, которые дают одинаковый MD5-хеш.
Таким образом, на данный момент MD5 официально неустойчив к поиску коллизий.
40. Алгоритм хеширования MD4 как средство решения задачи безопасного хранения паролей в ОС Windows: NT hash.
Задача безопасного хранения паролей подразумевает, что даже если криптоаналитик получил доступ к ОС и таблице хранимых проверочных значений паролей, он не может восстановить по ней настоящие «секретные» пароли. Одни из решений этой задачи является использования хэшей в качестве проверочных значений паролей, поскольку по хэшу невозможно восстановить секретный пароль. Однако, в таком случае остается возможно атаки на алгоритм хэширования с целью подобрать входное значение имеющее заданный хэш(проверочное значение искомого пароля). Эта атака в частности может быть осуществлена полным перебором.
NT хэш:
- Пароль пользователя переводится в Unicod
- Пароль хэшируется MD4
- По логину пользователя извлекается его уникальный идентификатор SID
- Из SID выбирается RID – часть идентификатора уникальная для пользователей в пределах компьютера(а вторая часть уникальная для разных компьютеров, но общая в пределах одного отбрасывается)
- MD4 хэш шифруется DES с использованием RID в качестве ключа
- Полученный результат является NT хэшем.
41. Алгоритм хеширования MD4 как средство решения задачи безопасного хранения паролей в ОС Windows: LM hash.
LM-хеш вычисляется следующим образом:
- Пароль пользователя как OEM-строка приводится к верхнему регистру.
- Пароль дополняется нулями или обрезается до 14 байтов
- Получившийся пароль разделяется на две половинки по 7 байтов.
- Эти значения используются для создания двух ключей DES, по одному для каждой 7-байтовой половинки, рассматривая 7 байтов как битовый поток и вставляя ноль после каждых 7 битов. Так создаются 64 бита, необходимые для ключа DES.
- Каждый из этих ключей используется для DES-шифрования ASCII-строки «KGS!@#$%», получая два 8-байтовых шифрованных значения.
- Данные шифрованные значения соединяются в 16-байтовое значение, являющееся LM-хешем.
Несмотря на то что LM-хеш основан на качественном блочном шифре DES, он может быть легко атакован для подбора пароля из-за двух уязвимостей в его реализации. Во-первых, пароли длиннее 7 символов разделяются на две части и каждая часть хешируется отдельно. Во-вторых, все символы нижнего регистра приводятся к верхнему до хеширования пароля. Первая уязвимость позволяет атаковать каждую часть пароля по отдельности. Хотя и существует 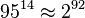 различных паролей составленных из видимых ASCII-символов, но можно составить только
различных паролей составленных из видимых ASCII-символов, но можно составить только  различных 7-байтовых частей пароля используя одну кодовую таблицу. Ограничение набора символов из-за преобразования к верхнему регистру также сокращает количество вариантов до
различных 7-байтовых частей пароля используя одну кодовую таблицу. Ограничение набора символов из-за преобразования к верхнему регистру также сокращает количество вариантов до 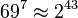 . Применив brute force атаку отдельно к каждой половине, современные персональные компьютеры могут подобрать буквенно-цифровой LM-хеш за несколько часов.
. Применив brute force атаку отдельно к каждой половине, современные персональные компьютеры могут подобрать буквенно-цифровой LM-хеш за несколько часов.
42. Решение задачи безопасного хранения паролей в ОС UNIX/Linux, понятие «соли», используемые алгоритмы хеширования.
В системе UNIX каждый пользователь имеет свой пароль и его знает только пользователь. Для защиты паролей используется хеширование. Предполагалось, что получить настоящий пароль можно только полным перебором. При появлении UNIX единственным способом хеширования был DES (Data Encryption Standard), но им могли пользоваться только жители США, потому что исходные коды DES нельзя было вывозить из страны. Во FreeBSD решили эту проблему. Пользователи США могли использовать библиотеку DES, а остальные пользователи имеют метод, разрешённый для экспорта. Поэтому в FreeBSD стали использовать MD5 по умолчанию. Некоторые Linux-системы также используют MD5 для хранения паролей.
Соль – уникальное значение для каждого пользователя, использующееся для того, чтобы при одинаковых паролях их хэши не совпадали.
Таблицы паролей хранятся либо в /etc/shadow, либо в /etc/master.password
Формат записей в таблице: login:salt$hash
Кроме упомянутых выше MD5 и DES для хэширования также иногда применяется SHA.
43. Алгоритм хеширования SHA-1: параметры, алгоритм забивки, алгоритм изменения переменных сцепления, раунды и операции, функции раундов.
Параметры:
- Длина хэша: 160 бит.
- Количество раундов: 80 (4 по 20).
- Длина хэшируемого сообщения: произвольная (L).
- Размер блока хэшируемого сообщения: 512 бит
Алгоритм забивки(идентичен алгоритму забивки MD5):
- Сначала дописывают единичный бит в конец потока (байт 0x80), затем необходимое число нулевых бит. Входные данные выравниваются так, чтобы их новый размер
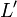 был сравним с 448 по модулю 512 (
был сравним с 448 по модулю 512 (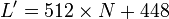 ). Выравнивание происходит, даже если длина уже сравнима с 448.
). Выравнивание происходит, даже если длина уже сравнима с 448.
- В оставшиеся 64 бита дописывают 64-битное представление длины данных (количество бит в сообщении) до выравнивания. Сначала записывают младшие 4 байта. Если длина превосходит
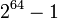 , то дописывают только младшие биты. После этого длина потока станет кратной 512. Вычисления будут основываться на представлении этого потока данных в виде массива слов по 512 бит.
, то дописывают только младшие биты. После этого длина потока станет кратной 512. Вычисления будут основываться на представлении этого потока данных в виде массива слов по 512 бит.
Алгоритм изменения переменных сцепления:
- Начальное значение переменных задается, как
A = a = 0x67452301
B = b = 0xEFCDAB89
C = c = 0x98BADCFE
D = d = 0x10325476
E = e = 0xC3D2E1F0
- Выбирается 512-битный блок из входного потока. Он преобразуется из 15 32-битных слов в массив из 80 32-битных слов:
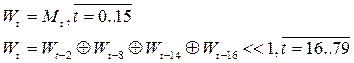
- Проходят 4 раунда по 20 проход, согласно схеме. Функция и константа K меняется каждый раунд согласно таблице. Значение W меняется каждый проход(от 0 до 79)/
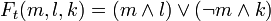
|  = 0x5A827999 = 0x5A827999
| 1 раунд |

|  = 0x6ED9EBA1 = 0x6ED9EBA1
| 2 раунд |

|  = 0x8F1BBCDC = 0x8F1BBCDC
| 3 раунд |

|  = 0xCA62C1D6 = 0xCA62C1D6
| 4 раунд |
Схема раунда:

- Отдельно хранится сумма результатов всех итераций (один 512-битный блок обрабатывается в рамках 1 итерации) для каждого из пяти регистров. Когда все блоки обработаны – эти 5 32-битных сумм вместе составят 160-битный хэш.
44. Антивирусное ПО: сигнатурные базы и алгоритмы хеширования. Утверждение Cohen о невозможности создать идеальный антивирус и проблема остановки в теории вычислимости.
45. Функции хеширования, основанные на симметричных шифрах. Алгоритм ГОСТ Р34.11-94: параметры, сжимающая функция и ее результат (имитовставка), генерация ключей, шифрующее преобразование, перемешивающее преобразование.
В качестве сжимающей функции можно использовать симметричный блочный алгоритм шифрования. Для обеспечения большей безопасности можно использовать в качестве ключа блок данных предназначенный к хешированию на данной итерации, а результат предыдущей сжимающей функции в качестве входа. Тогда результатом последней итерации будет выход алгоритма. В таком случае безопасность хеш-функции базируется на безопасности используемого алгоритма.
Основным недостатком хеш-функций, спроектированных на основе блочных алгоритмов, является низкая скорость работы.
Алгоритм ГОСТ Р34.11-94:
Параметры:
- Длина хэша: 256 бит.
- Количество раундов: 1
- Длина хэшируемого сообщения: произвольная (L).
- Размер блока хэшируемого сообщения: 256 бит
- Для алгоритма должны указываться 8 S-блоков для шифрующего преобразования ГОСТ 28147-89
Основой описываемой хеш-функции является шаговая функция хеширования 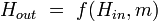 где
где  ,
, 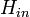 ,
, 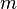 — блоки длины 256 бит.
— блоки длины 256 бит.
Основной алгоритм
- Входное сообщение
 разделяется на блоки
разделяется на блоки 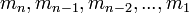 по 256 бит. В случае если размер последнего блока
по 256 бит. В случае если размер последнего блока  меньше 256 бит, то к нему приписываются слева нули для достижения заданной длины блока.
меньше 256 бит, то к нему приписываются слева нули для достижения заданной длины блока. - Каждый блок сообщения, начиная с первого, подаётся на шаговую функцию для вычисления промежуточного значения хеш-функции:
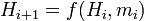
Значение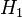 можно выбрать произвольным.
можно выбрать произвольным. - После вычисления
 конечное значение хеш-функции получают следующим образом:
конечное значение хеш-функции получают следующим образом:
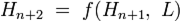 , где L — Длина сообщения M в битах по модулю
, где L — Длина сообщения M в битах по модулю 
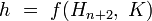 ,
,
где K — Контрольная сумма сообщения M:


Шаговая функция хэширования – сжимающая функция: преобразует два 256-битных значения в одно 256-битное значение состоит из трех частей:
- Генерирование ключей

- Шифрующее преобразование — шифрование
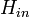 с использованием ключей
с использованием ключей 
- Перемешивающее преобразование результата шифрования
Генерация ключей:
Алгоритм:
1. 
2. Для j = 2,3,4 выполняем следующее:

Где:
C2 = 0
C3 = 0xff00ffff000000ffff0000ff00ffff0000ff00ff00ff00ffff00ff00ff00ff00
C4 = 0
Преобразование  , где
, где  — подблоки блока Y длины 64 бит.
— подблоки блока Y длины 64 бит.
Преобразование 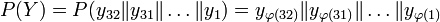 , где
, где 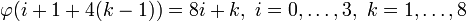 , а
, а 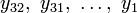 — подблоки блока Y длины 8 бит.
— подблоки блока Y длины 8 бит.
Шифрующее преобразование:
После генерирования ключей происходит шифрование 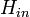 по ГОСТ 28147—89 в режиме простой замены на ключах
по ГОСТ 28147—89 в режиме простой замены на ключах 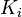 (для
(для 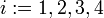 ), процедуру шифрования обозначим через E (Примечание: функция шифрования E по ГОСТ 28147 шифрует 64 битные данные 256 битным ключом). Для шифрования
), процедуру шифрования обозначим через E (Примечание: функция шифрования E по ГОСТ 28147 шифрует 64 битные данные 256 битным ключом). Для шифрования 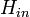 разделяют на четыре блока по 64 бита:
разделяют на четыре блока по 64 бита: 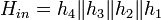 и зашифровывают каждый из блоков:
и зашифровывают каждый из блоков:
После чего блоки собирают в 256 битный блок: 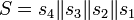
Перемешивающее преобразование:

: 
46. Алгоритм хеширования Keccak: параметры, алгоритм забивки, sponge-конструкция и фазы работы алгоритма, функция псевдослучайной перестановки. Использование алгоритма Keccak в качестве поточного шифра.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1735; Нарушение авторских прав?; Мы поможем в написании вашей работы!