Алгоритмы факторизации

Корректность схемы RSA

Шифрование и дешифрование

Предположим, Боб хочет послать Алисе сообщение .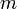

Сообщениями являются целые числа в интервале от до , т.е .

Алгоритм: § Взять открытый ключ Алисы § Взять открытый текст 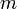§ Зашифровать сообщение с использованием открытого ключа Алисы:

Алгоритм: § Принять зашифрованное сообщение § Взять свой закрытый ключ § Применить закрытый ключ для расшифрования сообщения:

Уравнения и , на которых основана схема RSA, определяют взаимно обратные преобразования множества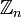

В зависимости от сложности алгоритмы факторизации можно разбить на две группы. Первая группа — экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входящих параметров (то есть от длины самого числа в бинарном представлении). Вторая группа — субэкспоненциальные алгоритмы, для обозначения сложности которых принята L-нотация:

где N — число подлежащее факторизации, и c — некоторые константы.

Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории чисел. В то же время факторизация с полиномиальной сложностью возможна на квантовом компьютере с помощью алгоритма Шора (класс BQP).

Дата добавления: 2015-04-24