Недостатки. Противодействия online атакам по словарю

Замечания

Противодействия online атакам по словарю

Основные противодействия атакам по словарю

Существует несколько способов противостоять online атакам по словарю:

1. задержка ответа (англ. delayed response): для предоставленной пары login/password сервер использует небольшую, специально сгенерированную задержку ответа Yes/no (например, не чаще одного ответа в секунду);

2. блокировка учетной записи (англ. account locking): учетная запись блокируется после нескольких (заранее установленное число) неудачных попыток ввода login/password (для примера, учетная запись блокируется на час после пяти неправильных попыток ввода пароля).

1. данные меры, в большинстве случаев, предотвращают атаку по словарю и сопутствующий взлом пароля за допустимое время;

2. данные реализации противодействия online атакам по словарю допускают долговременные блокировки пользовательских аккаунтов при правильном подборе периода атаки.

§ Преимущество алгоритма симметричного шифрования над несимметричным заключается в том, что в первый относительно легко внести изменения.

§ Хотя сообщения надежно шифруются, но «засвечиваются» получатель и отправитель самим фактом пересылки шифрованного сообщения.^[8]

§ Несимметричные алгоритмы используют более длинные ключи, чем симметричные. Ниже приведена таблица, сопоставляющая длину ключа симметричного алгоритма с длиной ключа несимметричного алгоритма (RSA) с аналогичной криптостойкостью:

§

Длина симметричного ключа, бит	Длина несимметричного ключа, бит

§ Процесс шифрования-расшифрования с использованием пары ключей проходит на два-три порядка медленнее, чем шифрование-расшифрование того же текста симметричным алгоритмом.

§ В чистом виде асимметричные криптосистемы требуют существенно больших вычислительных ресурсов, потому на практике используются в сочетании с другими алгоритмами.

1. Для ЭЦП сообщение предварительно подвергается хешированию, а с помощью асимметричного ключа подписывается лишь относительно небольшой результат хеш-функции.

2. Для шифрования они используются в форме гибридных криптосистем, где большие объёмы данных шифруются симметричным шифром на сеансовом ключе, а с помощью асимметричного шифра передаётся только сам сеансовый ключ.

48. Алгоритм Diffie–Hellman и задача нахождения дискретного логарифма. Пример выработки общего ключа. Атака типа «человек посередине» на алгоритм Diffie– Hellman.

Алгори́тм Ди́ффи — Хе́ллмана (англ. Diffie-Hellman, DH) — алгоритм, позволяющий двум сторонам получить общий секретный ключ, используя незащищенный от прослушивания, но защищённый от подмены канал связи. Этот ключ может быть использован для шифрования дальнейшего обмена с помощью алгоритма симметричного шифрования.

Алгоритм был впервые опубликован Уитфилдом Диффи (Whitfield Diffie) и Мартином Хеллманом в 1976 году.

В 2002 году Хеллман предложил называть данный алгоритм «Диффи — Хеллмана — Меркля», признавая вклад Меркля в изобретение криптографии с открытым ключом.

Предположим, что обоим абонентам известны некоторые два числа g и p (например, они могут быть «зашиты» в программное обеспечение), которые не являются секретными и могут быть известны также другим заинтересованным лицам. Для того, чтобы создать неизвестный более никому секретный ключ, оба абонента генерируют большие случайные числа: первый абонент — число a, второй абонент — число b. Затем первый абонент вычисляет значение 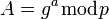и пересылает его второму, а второй вычисляет 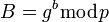и передаёт первому. Предполагается, что злоумышленник может получить оба этих значения, но не модифицировать их (то есть у него нет возможности вмешаться в процесс передачи). На втором этапе, первый абонент на основе имеющегося у него 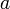и полученного по сети 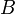вычисляет значение 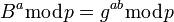, а второй абонент на основе имеющегося у него 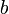и полученного по сети 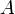вычисляет значение 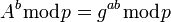. Как нетрудно видеть, у обоих абонентов получилось одно и то же число: 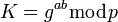. 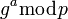Его они и могут использовать в качестве секретного ключа, поскольку здесь злоумышленник встретится с практически неразрешимой (за разумное время) проблемой вычисления по перехваченным и 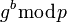, если числа выбраны достаточно большими.

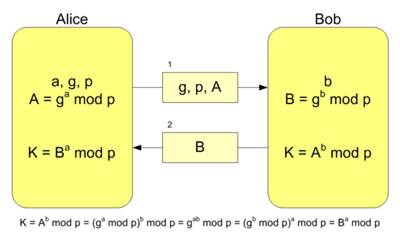
Алгоритм Диффи — Хеллмана, где K — итоговый общий секретный ключ

При работе алгоритма, каждая сторона:

1. генерирует случайное натуральное число a — закрытый ключ

2. совместно с удалённой стороной устанавливает открытые параметры p и g (обычно значения p и g генерируются на одной стороне и передаются другой), где

p является случайным простым числом

g является первообразным корнем по модулю p

3. вычисляет открытый ключ A, используя преобразование над закрытым ключом

A = g^a mod p

4. обменивается открытыми ключами с удалённой стороной

5. вычисляет общий секретный ключ K, используя открытый ключ удаленной стороны B и свой закрытый ключ a

K = B^a mod p

К получается равным с обеих сторон, потому что:

B^a mod p = (g^b mod p)^a mod p = g^ab mod p = (g^a mod p)^b mod p = A^b mod p

В практических реализациях, для a и b используются числа порядка 10¹⁰⁰ и p порядка 10³⁰⁰. Число g не обязано быть большим и обычно имеет значение в пределах первого десятка.

[править]Пример

Ева - криптоаналитик. Она читает пересылку Боба и Алисы, но не изменяет содержимого их сообщений.

§ s = секретный ключ. s = 2

§ g = открытое простое число. g = 5

§ p = открытое простое число. p = 23

§ a = секретный ключ Алисы. a = 6

§ A = открытый ключ Алисы. A = g^a mod p = 8

§ b = секретный ключ Боба. b = 15

§ B = открытый ключ Боба. B = g^b mod p = 19

Алиса
знает	не знает
p = 23	b =?
g = 5
a = 6
A = 5^6 mod 23 = 8
B = 5^b mod 23 = 19
s = 19^6 mod 23 = 2
s = 8^b mod 23 = 2
s = 19^6 mod 23 = 8^b mod 23
s = 2

Боб
знает	не знает
p = 23	a =?
g = 5
b = 15
B = 5^15 mod 23 = 19
A = 5^a mod 23 = 8
s = 8^15 mod 23 = 2
s = 19^a mod 23 = 2
s = 8^15 mod 23 = 19^a mod 23
s = 2

Ева
знает	не знает
p = 23	a =?
g = 5	b =?
	s =?
A = 5^a mod 23 = 8
B = 5^b mod 23 = 19
s = 19^a mod 23
s = 8^b mod 23
s = 19^a mod 23 = 8^b mod 23

[править]Шифрование с открытым ключом

Данный алгоритм может также использоваться в качестве алгоритма шифрования с открытым ключом. В этом случае общая схема остаётся аналогичной приведённой выше, но с небольшими отличиями. Алиса не передаёт значения p, g и A Бобу напрямую, а публикует их заранее в качестве своего открытого ключа. Боб выполняет свою часть вычислений, после чего шифрует сообщение симметричным алгоритмом, используя K в качестве ключа, и передаёт шифротекст Алисе вместе со значением B. Однако такой подход не получил распространения, в этой области доминирует алгоритм RSA.

Дата добавления: 2015-04-24