Площади плоских фигур

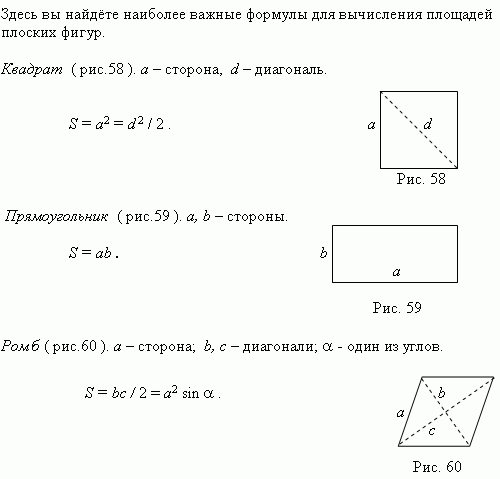
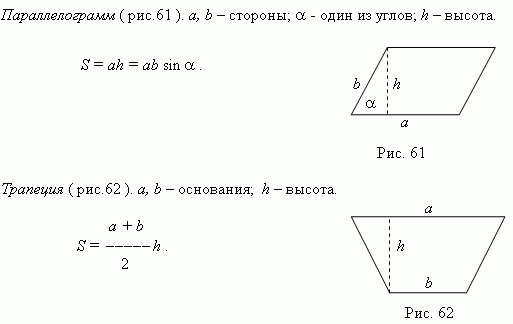
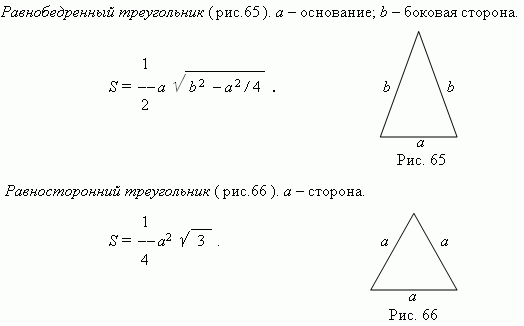
Произвольный треугольник. a, b, c – стороны; a – основание; h – высота;

A, B, C – углы, противоположные сторонам a, b, c; p = (a + b + c) / 2.

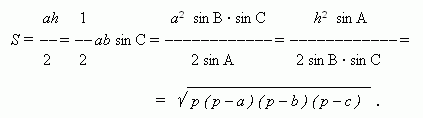
Последнее выражение называется формулой Герона.

Многоугольник, площадь которого нужно определить,может быть разделён своими диагоналями на несколько треугольников. Многоугольник, описанный около круга (рис.67), может быть разделён прямыми, идущими из центра круга к его вершинам. Тогда получаем:

В частности, эта формула справедлива для любого правильного многоугольника.

Правильный шестиугольник. a – сторона.

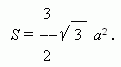
Круг. D – диаметр; r – радиус.

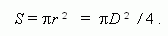
Сектор (рис.68). r – радиус; n – величина центрального угла в градусах; l – длина дуги.

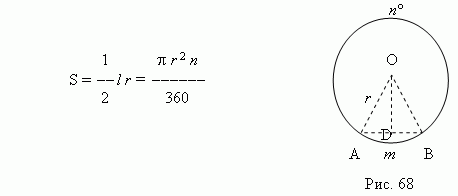
Сегмент (рис.68).Площадь сегмента определяется как разность между площадями сектора A m BO и треугольника AOB. Кроме того, есть приближённая формула для площади сегмента:

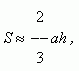
35.

Длина дуги окружности

Длина дуги окружности, как и длина произвольной кривой (спрямляемой), по определению равна пределу длин вписанных в нее ломаных при неограниченном возрастании числа звеньев и наибольшей длине звена, стремящейся к нулю. В случае окружности в определении можно ограничиться, например, последовательностью ломаных со звеньями равной длины, число которых на каждом шагу удваивается. Длина дуги радиуса R с радианной мерой α (см. Дуга окружности) равна R α. Через градусную меру n длина дуги выражается формулой .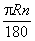

36. Формулы объема геометрических тел

Дата добавления: 2015-04-24