
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Средневековая схоластика: философские проблемы, идеи и представители
|
|
|
|
.
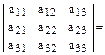

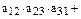

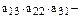
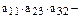
 .
.
- Ранг матрицы. Определение ранга матрицы через миноры и линейную независимость строк (столбцов) матрицы.
Минором 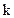 – го порядка матрицы А называют определитель матрицы
– го порядка матрицы А называют определитель матрицы 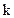 – го порядка, которая получается из матрицы А вычеркиванием всех строк и столбцов, кроме отмеченных произвольным образом
– го порядка, которая получается из матрицы А вычеркиванием всех строк и столбцов, кроме отмеченных произвольным образом 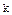 строк и столбцов.
строк и столбцов.
Рангом ненулевой матрицы называется максимальный порядок ее ненулевого минора.
Обозначение:  . Ранг нулевой матрицы по определению полагают равным нулю.
. Ранг нулевой матрицы по определению полагают равным нулю.
Ранг матрицы равен рангу системы ее строк и равен рангу системы ее столбцов.
- Обратная матрица, определение и вычисление.
Матрица А-1 называется обратной к матрице А, если А∙А-1 = А-1 ∙А = Е.
Для того чтобы квадратная матрица была обратимой необходимо и достаточно, чтобы ее определитель был не равен нулю.
Обратная матрица может быть найдена по формуле:  .
.
- Решение систем. Случай однозначного разрешения. Метод Крамера.
Пусть дана система из m линейных уравнений с n неизвестными: 
 . Матрица А, элементами которой являются соответствующие коэффициенты линейных уравнений системы называется матрицей этой системы.
. Матрица А, элементами которой являются соответствующие коэффициенты линейных уравнений системы называется матрицей этой системы.
Столбец 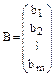 называется столбцом свободных членов системы.
называется столбцом свободных членов системы.
Матрица  называется расширенной матрицей системы и обозначается
называется расширенной матрицей системы и обозначается  . Столбец
. Столбец  называется столбцом неизвестных системы.
называется столбцом неизвестных системы.
Формулы Крамера: Пусть  квадратная система линейных уравнений и
квадратная система линейных уравнений и  . Тогда единственное решение системы можно найти по формулам:
. Тогда единственное решение системы можно найти по формулам:
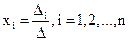 ,
,
где

– определитель матрицы системы,  – столбцы матрицы системы,
– столбцы матрицы системы,
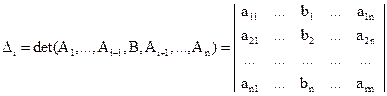
– определитель системы, в котором i-й столбец заменен столбцом свободных членов В.
- Совместные, несовместные системы. Теорема Кронекера-Капели.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение и несовместной в противном случае.
Совместная система линейных уравнений называется определенной, если она имеет единственное решение и неопределенной, если она имеет более одного решения.
Замечание. Легко видеть, что однородная система линейных уравнений  является совместной, т.к. она всегда имеет нулевое решение.
является совместной, т.к. она всегда имеет нулевое решение.
Теорема (Кронекер – Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы. Другими словами, если  – система линейных уравнений, то для того, чтобы данная система имела хотя бы одно решение необходимо и достаточно, чтобы
– система линейных уравнений, то для того, чтобы данная система имела хотя бы одно решение необходимо и достаточно, чтобы  .
.
- Линейно зависимая и линейно независимая система векторов.
Выражение  , где
, где 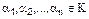 - скаляры поля К,
- скаляры поля К, 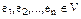 – векторы векторного пространства V, называется линейной комбинацией системы векторов
– векторы векторного пространства V, называется линейной комбинацией системы векторов  .
.
Система векторов  векторного пространства V называется линейно зависимой, если найдется такой ненулевой набор скаляров поля K
векторного пространства V называется линейно зависимой, если найдется такой ненулевой набор скаляров поля K 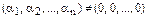 , что
, что  , иначе - линейно независимой.
, иначе - линейно независимой.
Система векторов 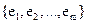 векторного пространства V над полем K называется системой образующих, если она представляет любой его вектор, т.е.
векторного пространства V над полем K называется системой образующих, если она представляет любой его вектор, т.е.
 .
.
- Векторное пространство. Базис векторного пространства.
Пусть V – произвольное непустое множество, элементы которого мы будем называть векторами, K – поле, элементы которого мы будем называть скалярами. Пусть на множестве V определена внутренняя бинарная алгебраическая операция, которую мы будем обозначать знаком + и называть сложением векторов. Пусть также на множестве V определена внешняя бинарная алгебраическая операция, которую мы будем называть умножением вектора на скаляр и обозначать знаком умножения.
Пусть, другими словами, определены два отображения:
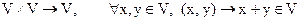 ;
;
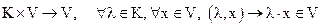 .
.
Множество  вместе с этими двумя алгебраическими операциями называется векторным пространством над полем К, если выполняются следующие аксиомы:
вместе с этими двумя алгебраическими операциями называется векторным пространством над полем К, если выполняются следующие аксиомы:
1. Сложение ассоциативно, т.е.
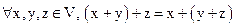 .
.
2. Существует нулевой вектор, т.е.
 .
.
3. Для любого вектора существует противоположный ему:
 .
.
Вектор у, противоположный вектору х, обычно обозначается –х, так что
 .
.
4. Сложение коммутативно, т.е.  .
.
5. Умножение вектора на скаляр подчиняется закону ассоциативности, т.е.
 ,
,
где произведение  есть произведение скаляров, определенное в поле К.
есть произведение скаляров, определенное в поле К.
6. 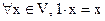 , где 1 – единица поля К.
, где 1 – единица поля К.
7. Умножение вектора на скаляр дистрибутивно относительно сложения векторов:
 .
.
8. Умножение вектора на скаляр дистрибутивно относительно сложения скаляров:
 .
.
Упорядоченная система векторов 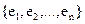 векторного пространства V над полем K называется его базисом, если для любого его вектора
векторного пространства V над полем K называется его базисом, если для любого его вектора  существует единственный упорядоченный набор скаляров
существует единственный упорядоченный набор скаляров 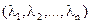 поля K, такой, что верно равенство
поля K, такой, что верно равенство 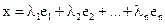 .
.
Теорема. Для того чтобы система векторов векторного пространства была базисом, необходимо и достаточно, чтобы она была линейно независимой системой образующих.
Размерностью векторного пространства V называется число векторов в его базисе и обозначается 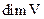 .
.
- Линейное отображение. Матрица линейного отображения.
Пусть V и W – произвольные векторные пространства над полем K. Отображение f: V→W называется линейным отображением или гомоморфизмом векторного пространства V в векторное пространство W, если оно обладает свойствами линейности:
1) 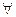 x, y
x, y  V, f(x+y)=f(x)+f(y); 2)
V, f(x+y)=f(x)+f(y); 2) 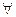 x
x  V,
V, 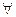

 K, f(
K, f( x)=
x)=  f(x).
f(x).
Если, кроме этого, гомоморфизм является биективным отображением, то он называется изоморфизмом векторных пространств и.
- Ядро и образ линейного отображения.
Ядром линейного отображения
- Собственные числа и собственные векторы линейного оператора.
- Евклидово пространство. Норма вектора. Ортогональный базис евклидова пространства.
- Алгебраическая, тригонометрическая и показательная форма записи комплексного числа. Их взаимосвязь.
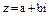 – алгебраическая форма записи комплексного числа. Элемент i называется мнимой единицей.
– алгебраическая форма записи комплексного числа. Элемент i называется мнимой единицей.
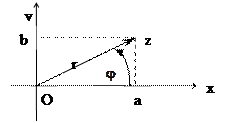
Если точка z комплексной плоскости имеет декартовые координаты (х, у), т.е. 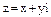 и полярные
и полярные 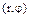 , то они связаны соотношением:
, то они связаны соотношением:  .
. 
По определению,  и получаем:
и получаем:  .
.
Подставляя в алгебраическую форму записи числа z получаем: 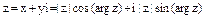 . Или
. Или  , где
, где  .
.
- Операции над комплексными числами: сложение, умножение, деление, возведение в степень.
Пусть  – два произвольных комплексных числа.
– два произвольных комплексных числа.
Тогда  ;
; 
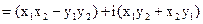 ;
;
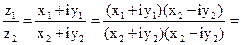 …
…  .
.
Пусть  ,
,  .
.
Тогда 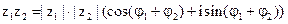 .
.
Чтобы разделить одно комплексное число на другое, нужно модуль числителя разделить на модуль знаменателя и из аргумента числителя вычесть аргумент знаменателя.
Формула Муавра: 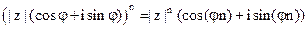 .
.
- Корни n-ой степени из комплексного числа и их геометрическая интерпретация.
Пусть n натуральное число. Комплексное число  называется корнем n-й степени из комплексного числа z, если
называется корнем n-й степени из комплексного числа z, если  .
.
Существует ровно n корней n-й степени из комплексного числа z и все они могут быть найдены по формуле:
 , где
, где  ,
,  .
.
Из формулы корней мы видим, что все корни 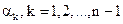 имеют одинаковый модуль
имеют одинаковый модуль 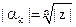 . Следовательно, на комплексной плоскости все они расположены на окружности с центром в начале координат и радиуса
. Следовательно, на комплексной плоскости все они расположены на окружности с центром в начале координат и радиуса 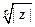 .
.
Обозначим аргумент k-го корня через 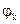 . Тогда из формулы (1) следует, что
. Тогда из формулы (1) следует, что
 . (2)
. (2)
Заметим, что аргументы корней образуют арифметическую прогрессию с разностью  и первым членом прогрессии
и первым членом прогрессии 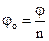 , т.е. имеет место формула
, т.е. имеет место формула
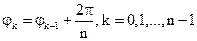 . (3)
. (3)
Таким образом, корни расположены на окружности равномерно, через равные промежутки и разбивают окружность на n равных дуг. Другими словами, точки окружности, отождествленные с корнями являются вершинами правильного n-угольника. Вершины правильного n-угольника называются точками деления окружности (круга), описанной около данного многоугольника.
Первообразные корни n-ой степени из 1. Пусть 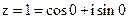 . Тогда, применяя формулу корней n-й степени из комплексного числа, получаем:
. Тогда, применяя формулу корней n-й степени из комплексного числа, получаем: 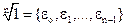 ,
,
где обозначено 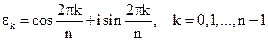 .
.
Из этой формулы мы видим, что  .
.
Таким образом, все n корней n-й степени из 1 расположены на комплексной плоскости на единичной окружности, которую можно рассматривать как тригонометрическую окружность, делят ее на n равных дуг, равных по  радиан, причем
радиан, причем  – одна из n точек деления круга. Соединив все последовательные (соседние) точки
– одна из n точек деления круга. Соединив все последовательные (соседние) точки 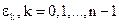 отрезками прямых, мы получаем правильный n-угольник.
отрезками прямых, мы получаем правильный n-угольник.
Определение. Корень n-й степени из 1 называется первообразным корнем n-й степени из 1, если все корни из 1 являются его степенями.
Следствие. Корень n-й степени из 1,  является первообразным корнем n-й степени из 1.
является первообразным корнем n-й степени из 1.
Теорема. Корень n-й степени из 1, 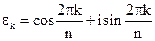 является первообразным корнем n-й степени из 1 тогда и только тогда, когда
является первообразным корнем n-й степени из 1 тогда и только тогда, когда 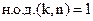 .
.
- Группа, кольцо, поле.
- Трехгранник Френе. Касательная, главная нормаль, бинормаль.
- Кривизна и кручение.
- Касательная плоскость к поверхности, нормаль поверхности.
- Замыкание, внутренность, граница множества.
- Компактное пространство. Критерий компактности пространства из Rn.
Схоластика
По мере завершения работы по оформлению догматических основ христианства патристика постепенно переходит в схоластику. Патристика боролась с язычеством и пропагандировала этико-религиозную доктрину христианства в мире, еще не вполне принявшем новую религию и утверждающую его мораль. Схоластика, опираясь на авторитет Священного писания, философские идеи патристики, стремится включить в обиход философствования наследие языческой античности и прежде всего наследия Платона, Аристотеля, Плотина и Прокла. Делает это она для того, чтобы осмыслить и рационализировать окружающую человека действительность. Одной из важнейших проблем схоластики выступает проблема соотношения мира рационального знания и мира духовного опыта. Решение этой проблемы требовало соотношения разума и веры. Представители схоластики, размышляя об этом соотношении, пришли к выводу о том, что вера и разум должны находиться в гармоническом единстве друг с другом. Дело в том, что разум при надлежащем использовании ведет к приближению к Богу, к единению с Ним. Иными словами, истины разума и веры не могут противоречить друг другу. Такова суть одного из главных выводов схоластической средневековой философии.
Наиболее крупными представителями средневековой схоластики считаются Иоанн Скот Эриугена (ок. 810 – ок. 877), Ансельм Кентерберийский (1033 – 1109), Бонавентура (1221 – 1274), Фома Аквинский (1225 – 1274), Дунс Скот (1266 – 1308) и Уильям Оккам (1300 – 1349)
Схоласты считали, что сущность вещей может быть постигнута человеческим разумом. Однако это требует точности в использовании языка и тонкости понимания различий вещей. Этого можно достичь лишь при наличии основательно разработанного, опирающегося на знание логики метода. Суть схоластического метода сводится к тому, чтобы обеспечивать движение мысли от анализа способов высказывания о сущем, к анализу реальности. При этом схоластика исходит из убеждения, согласно которому понятия укоренены не только в человеческом разуме, но и в Божественном уме, созидающем бытие. Иными словами, понятие рассматривается как бы существующим двойным способом в уме человека и в бытии. Ключом к постижению мира считается постижение универсалий.
Фома Аквинский (1225/ 1226 – 1274) считается самым крупным представителем схоластической философии, основными принципами которой выступают принцип разъяснения и принцип принятия и согласования противоположных тенденций.
По мнению Фомы Аквинского, отношение к выдающимся предшественникам наряду со знанием Библии является основой преподавания философии. Такая установка побудила его написать ряд комментариев к трудам философов прошлого (Боэция, Аристотеля). Но главными его философскими сочинениями стали «Сумма против язычников» и «Сумма теологии». Особенностью философии Фомы Аквинского является то, что он высоко ценил идеи Аристотеля, стремился дать им такую интерпретацию, чтобы создать последовательную систему, связанную с утверждением христианской веры. Своим современникам Фома казался новатором, так как в какой-то мере дал новую трактовку традиционно рассматривавшимся философами проблемам и ввел в употребление новые способы, приемы аргументации, а также отверг некоторые традиционные подходы к осмыслению некоторых вопросов. Он не стремился прослыть оригиналом, но новизна в его мысли имела место. Она проявлялась в том, что он терпеливо анализировал разные мнения, стремясь достичь истины и систематически синтезировал разные позиции, используя для этого всеобъемлющие философские принципы и категории.
Фома Аквинский стремился использовать философию для обоснования и доказательства истин веры. Он считал, что философская теология является высшим выражением философской рефлексии.
Согласно представлениям Фомы, предметом философии являются истины разума, а предметом теологии – истины откровения. Конечным объектом философии и теологии является Бог, выступающий создателем мира и вдохновителем его развития. Бог, по учению Фомы, представляет собой вечное, наисовершеннейшее духовное существо, это – чистая форма, источник всех возможных форм, благодаря которой из пассивной материи возникают самые разнообразные вещи.
В произведении «Сумма теологии» приводятся пять доказательств существования Бога: 1) Бог рассматривается как «неподвижный двигатель», приводящий все в движение; 2) Бог рассматривается как первая причина; 3) Бог является источником необходимости в мире; 4) Бог есть источник совершенства, сам являясь совершенным; 5) Бог устанавливает конечные цели и поэтому не может не существовать.
Фома считал Бога благом и источником блага. Бог, по мнению христианского мыслителя, вездесущ и выступает источником любви и радости. Он добр и ему чуждо чувство ненависти.
Согласно учению Фомы, люди и животные обладают душами, но человеческие души отличаются от душ животных, так как первые являются разумными, а вторые чувственными. Однако даже человеческая душа лишена способности непосредственного содержания Бога и Божественных идей, но ей открыт путь рационального познания.
Фома полагал, что человек ищет счастья по своей природе как существо, стремящееся реализовать свои потенции. Наивысшее счастье человека мыслитель видит в познании Бога. На этом пути человек должен сознательно избрать бедность, облегчающую путь к Богу. Этому способствует следование Божеским установлениям, в соответствии с которыми должен жить и действовать каждый христианин. Моральные заповеди, дарованные Богом, рассматриваются как рациональные. Нормативное содержание моральных заповедей обращено к разуму человека, который должен этим содержанием овладеть. Главная задача морального закона, раскрывающегося в заповедях христианской морали, регулятивная. Он шаг за шагом ведет человека по пути добродетели. При этом высшее назначение человека выходит за пределы естественного порядка. Следовательно, человеку необходимо сверхъестественное руководство. При этом знание морального закона переходит в добродетели благодаря желанию добра, а не воздействия страха. Движение к добродетели должно осуществляться благодаря любви и Богу, как законодателю и творцу всего сущего.
Фома немало сделал для обоснования божественного происхождения власти монарха и необходимости подчинения простых людей господам. В то же время он доказывал, что светской власти подчиняются только тела людей, а не их души. Души должны, по его мнению, направлять к Богу церковь.
Западная христианская философия развивалась в полемике между сторонниками разных точек зрения на соотношения общего и единичного. Схоласты предложили несколько решений этого вопроса. Основных решений данного вопроса было два. Первое, отстаивавшееся Иоганом Скотом (Эриугеной) (810 – 877), Ансельмом Кентерберийским (1033 – 1109), Альбертом Великим и Фомой Аквинским, состояло в утверждении, что общее или «универсалии существуют реально, независимо от человеческой мысли речи», подобно платоновским идеям. Взгляд этот получил название «реализма».
Так, Фома Аквинский доказывал, что универсалии существуют до вещей как реальные прообразы индивидуальных предметов в Божественном разуме, где они возникают как понятия путем абстрагирования от отдельных вещей. Первичными и общими, следовательно, являются Божественные универсалии, а вторичными – материальные вещи.
Другое решение проблемы соотношения общего и единичного было предложено оппонентами реализма, получившими прозвание номиналистов.
Номиналисты (от латин. nomina – имена) доказывали, что реально существуют конкретные вещи, предметы, явления с их качествами и свойствами, а общее, понятия связаны лишь с человеческим сознанием. Это имена, которые человек дает вещам, группам и классам вещей. Одни номиналисты, например, Росцелин (ок. 1050 – 1110), Пьер Абеляр (1079 – 1142), Уильям Оккам (ок. 1300 – 1350) считали, что общее суть лишь дуновение звука, существует только в уме человека. В самих вещах нет ни ничего общего, ни частного. Другие, как, например, Дунс Скот (ок. 1265 – 1308) полагали, что общее не есть только продукт ума, оно имеет основание и в самих вещах, как их сущность, и после них, как понятия, которые наш ум отвлекает от этих сущностей.
Номинализм представлял собой умонастроение, содержащее зародыш материалистического понимания мира вещей. Не случайно поэтому в 1092 г. в Суассоне было осуждено церковным собором учение Росцелина, а в 1121 г. – учение Абеляра. Не следует забывать, что средневековый номинализм содержал лишь зародыши материализма, но не отрицал Бога и его могущества.
Уильям Оккам приобрел особую известность среди представителей номинализма в европейской средневековой схоластике. Ему принадлежит идея, согласно которой «сущности не следует умножать без необходимости». Эту идею он выразил на самом деле иначе, а именно: «Бессмысленно делать из большего то, что может быть сделано из меньшего». Данная идея получила в философии статус принципа, названного «бритвой Оккама». Согласно этому принципу, имея дело с предметами, важно установить, какие сущности явно присутствуют и далее необходимо формулировать высказывания в терминах этих сущностей.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1043; Нарушение авторских прав?; Мы поможем в написании вашей работы!