Вопрос№25. Часто встречаются группировки, где известна численность единиц в группах или удельный вес каждой группы в общем итоге

Часто встречаются группировки, где известна численность единиц в группах или удельный вес каждой группы в общем итоге. Такая группировка называется рядом распределения. Ряд распределения характеризуется двумя элементами:

1. Обозначение группы

2. Численность единиц в группах

Численность каждой группы называется частотами ряда распределения. Сумма всех частот определяет численность всей совокупности. Численность групп, выраженная в долях от общей численности единиц называется частостями и выражается в процентах.

Ряды распределения могут быть образованы по атрибутивному или количественному признакам. При группировке по атрибутивному признаку ряд распределения составляют отдельные группы, указываемые их наименованием и численность или удельный вес каждой группы в процентах к итогу.

При группировке данных по количественному признаку получаются ряды, называемые вариационными. В статистике различают вариационные ряды прерывные (дискретные) и непрерывные. Вариационный ряд будет дискретным, если его группы составлены по признаку изменяющемуся прерывно. Вариационный ряд называется непрерывным если группировочный признак, составляющий основание группировки может принимать в определенном интервале любые значения.

Статистические ряды распределения
Ряд распределения в статистике – это простейшая группировка, представляющая собой упорядоченное распределение единиц совокупности на группы по изучаемому варьирующему признаку.

По характеру изучаемого признака ряды подразделяются на атрибутивные (когда варьирующий признак качественный, т.е. не имеет количественного выражения) и вариационные (если изучаемый признак измеряется количественно).

В каждом ряду распределения выделяют два основных элемента:

- варианты 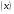- конкретные значения признака;

- частоты 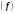- числа, показывающие, как часто встречаются данные варианты.

Если варианты представлены целыми значениями признака, то такие вариационные ряды распределения называются дискретными, а если варианты представлены числовыми интервалами, то такие ряды называются интервальными.

Ряды распределения дополняются частостями и накопленными (кумулятивными) частотами.

Частость - относительная частота, определяемая отношением числа единиц групп к общему объему совокупности.

Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше данного значения. Определяется последовательным прибавлением к частоте в первом интервале последующих частот ряда.

Величина интервала группировки интервального вариационного ряда определяется по формуле

,
где - максимальное значение признака, - минимальное значение признака, - число выделяемых групп.
При решении вопроса о том, сколько следует образовать групп, нужно принимать во внимание размах варьирования и численность единиц изучаемой совокупности. Чем больше размах варьирования признака, положенного в основу группировки, тем, как правило, больше может быть образовано групп.

Зависимость между числом групп и численностью единиц совокупности n можно выразить формулой американского ученого Стерджесса:

Эта зависимость может служить ориентировкой при определении числа групп в том случае, когда распределение единиц совокупности по данному признаку приближается к нормальному.

	15-24	25-44	45-89	90-179	180-359	360-719	720-1439
	5	6	7	8	9	10	11

Если, например, требуется произвести группировку с равными интервалами по данным о стоимости основных фондов предприятий, максимальное значение которой составляет 7 млн. руб., минимальная – 1 млн. руб. и необходимо выделить при этом 4 группы, то величина интервала определяется следующим образом

млн. руб.
В нашем примере группировка с равными интервалами примет такой вид

1 – 2,5

2,5 – 4

4 – 5,5

5,5 – 7

При такой записи следует помнить правило, что левая цифра включает в себя обозначенное значение, а правая не включает. Следовательно, предприятия с основными фондами 2,5 млн. руб. должно быть отнесено ко второй группе.

Проиллюстрируем построение ряда распределения на условном примере.

Пример 2.1. Имеются следующие данные о производственном стаже работников малого предприятия, лет.

9, 3, 7, 2, 5, 3, 11, 6, 5, 4, 7

Необходимо построить ряд распределения работников по стажу, обработав 3 группы с равными интервалами.

Решение.

Величина интервала группировки работников по стажу определяется по формуле
года
Тогда интервалы будут следующими:

2 – 5, 5 – 8, 8 – 11

Подсчитаем частоты и представим результаты в таблице, которую дополним частостями и кумулятивными частотами
Таблица 2.1. Ряд распределения работников по производственному стажу

Группы работников по стажу	Число работников, чел.	Число работников, % к итогу	Накопленная частота	Середина интервала
2 – 5 5- 8 8 - 11	4 5 2	36,4 45,4 18,2	4 9 11	3,5 6,5 8,5
Итого	11	100,0	-

Ряды распределения для наглядности и удобства анализа могут быть изображены графически. Основные виды графиков рядов распределения: полигон частот (Рис. 1), гистограмма (Рис. 2), кумулята (Рис. 3).

Для изображения построенного интервального ряда работников по производственному стажу в виде полигона частот следует превратить его в дискретный ряд. Для этого определить середины (центры) интервалов -

(3, 5; 6,5; 9,5). Из этих середин восстановить перпендикуляры равные частотам и соединить их вершины отрезками.
При построении гистограммы ряда распределения работников по стажу работы на оси абсцисс откладывают интервалы ряда, высота которых равна частотам отложенным по оси ординат. Над осью абсцисс строятся прямоугольники, площадь которых соответствует величинам произведений интервалов на их частоты.

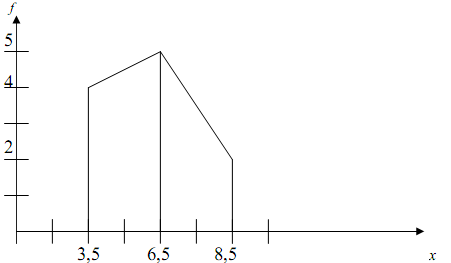
Рис. 2. Гистограмма ряда распределения работников по стажу работы
При графическом изображении кумуляты накопленные частоты наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов, а именно 5, 8, 11. Перпендикуляры затем соединяют отрезками, в результате чего получают ломаную линию, которая начинается от нуля все время возрастает, до тех пор, пока не достигнет высоты, равной общей сумме частот.

Рис. 3. Кумулята ряда распределения работников по стажу работы
Анализ ряда и графиков показывает, что распределение работников по стажу не является равномерным, чем больше стаж работников отличается от среднего стажа, тем реже такие работники встречаются.

Обобщение первичных данных в виде ряда распределения позволяет видеть вариацию и состав совокупности по изучаемому признаку, сравнивать между собой группы, изучать их динамику и устанавливать характер распределения единиц по тому или иному признаку.

Однако ряды распределения не дают всесторонней характеристики выделенных групп. Чтобы решить ряд конкретных задач, выявить особенности в развитии явлений, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных.

Как осуществляется конкретная группировка рассмотрим в следующем вопросе.
5. Осуществление конкретной аналитической группировки
Изучив задачи, особенности и технику построения рядов распределения, перейдем к применению метода группировки.

Пример 2.2 Имеются следующие условные данные о производственном стаже работников (из примера 1) и их среднесменной выработке изделий.
Таблица 2.2

№ работника по списку	Производственный стаж, лет	Среднесменная выработка изделий, шт
1 2 3 4 5 6 7 8 9 10 11	9 3 7 2 5 3 11 6 5 4 7	10 7 7 6 9 8 12 9 8 7 9

С целью выявления наличия, направления и характера взаимосвязи между выработкой и стажем работников необходимо:

1. провести аналитическую группировку, образовав три группы работников с равными интервалами

2. построить корреляционную таблицу, образовав три группы по обоим признакам
Решение

1. Поскольку аналитическая группировка предполагает разделение единиц совокупности на группы по факторному признаку, необходимо его определить.

В нашем примере факторным признаком является производственный стаж, так как от него зависит выработка. Определим величину интервала группировки по стажу работы.
г.
Тогда интервалы будут: 2-5; 5-8; 8-11.

Чтобы дополнить эти данные средними по группам значениями выработки изделий необходимо построить рабочую таблицу 3.
Таблица 2.3 Распределение работников по стажу

Группы работников по производственному стажу, г.	Номера и число работников, чел.	Стаж работы, г.	Выработка изделий, шт.
1	2	3	4
2-5	2 4 6 10	3 2 3 4	7 6 8 7
Всего	4	12	28
5-8	3 5 8 9 11	7 5 6 5 7	7 9 9 8 9
Всего	5	30	42
8-11	1 7	9 11	10 12
Всего	2	20	22
Итого	11	62	92

На основании итоговых данных рабочей таблицы 3 можно построить итоговую таблицу 4 аналитической группировки.
Таблица 2.4 Зависимость выработки изделий работниками от их производственного стажа

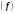Группы работников по производственному стажу, г.	Число работников	Выработка изделий, шт.
В целом по группе	В среднем на одного работника
А	1	2	3
2-5 5-8 8-11	4 5 2	28 42 22	4,000 8,400 11,000
Итого	11	92

Групповые средние и общую среднюю результативного признака определим по формуле простой средней арифметической.

Анализ таблицы показывает (см. гр А и 3 табл. 4), что с ростом производственного стажа от группы возрастает и средняя выработка работников. Следовательно, между производственным стажем и выработкой работников существует прямая корреляционная взаимосвязь.

2. Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному и результативному.

Концентрация частот около диагоналей матрицы данных свидетельствует о наличии и направлении (прямая, обратная) корреляционной связи между признаками. Построим корреляционную таблицу.

Для этого определим величины интервалов группировки и интервалы по факторному и результативному признакам 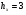интервалы 2-5, 5-8, 8-11.
шт; интервалы: 6-8, 8-10, 10-12.

Строим корреляционную таблицу 5.
Таблица 2.5 Распределение работников по производственному стажу и выработке изделий

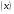Группы работников по производственному стажу, г.	Группы работников по выработке изделий, шт.
6-8	8-10	10-12	итого
2-5 5-8 8-11	3 1 -	1 4 -	- - 2	4 5 2
Итого	4	5	2	11

Как видно из таблицы 5 распределение числа работников произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, т.е. увеличение признака «производственный стаж» сопровождалось увеличением признака «выработка изделий». Характер концентрации частот по этой диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.

Дата добавления: 2015-04-24