Теорема Остроградского Гаусса и ее применение для вычисления напряженности простейших полей

Распределение зарядов в пространстве (плотность зарядов).

Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды.

На практике часто встречаются случаи, когда заряженное тело настолько велико, что использование модели точечного заряда не представляется возможным, в этом случае для определения параметров поля необходимо знать распределение зарядов внутри тела, т.е. по его объёму. В этом случае поступают по аналогии с определением плотности тела, весь объём тела V разбивается на большое количество элементарных объёмов ΔV, заряд которых будет Δq. В этом случае заряженность тела можно охарактеризовать объёмной плотностью заряда 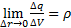– Объемная плотность.

Для целого класса веществ, например, для проводников, характерно присутствие электрических зарядов только в достаточно тонком поверхностном слое. В этом случае характерной величиной при анализе полей будет поверхностная плотность зарядов, которая по аналогии с уравнением определится как 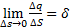– Поверхностная плотность заряда. Где dq — заряд, заключенный в слое площади dS, dS – физически бесконечно малый участок поверхности.

Проводники, длина которых существенно больше их прочих размеров удобно характеризовать линейной плотностью заряда 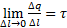– Линейная плотность заряда. Где dl — длина физически бесконечно малого отрезка цилиндра, dq — заряд, сосредоточенный на этом отрезке.

Теорема Остроградского Гаусса: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.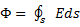

Плотность заряда — это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды.
Принцип применения:

¾ Строим гауссову поверхность

¾ Строим фигуру проходящую через поверхность

¾ Определяем напряженность (Е) или индукцию(D)

Гаусcова поверхность должна удовлетворять следующим критериям:

¾ Должная являться абстракцией

¾ Обязательно должна быть замкнута

¾ По возможности должна быть правильной геометрической формы

¾ Должна обязательно включать в себя заданные заряды.

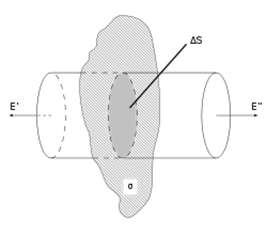Расчёт напряжённости поля бесконечной плоскости

Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosα = 0),то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания En совпадает с E), т.е. равен 2ES.

Заряд, заключенный внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса 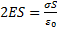, откуда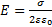

Из формулы вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.

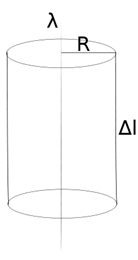Расчёт напряжённости поля бесконечной нити

Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной 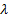. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой . Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицах СИ):

В силу симметрии:

1. вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней).

2. модуль этого вектора в любой точке поверхности цилиндра одинаков.

Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:

Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления E по касательной к ним). Приравнивая два полученных выражения для 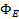, имеем:

Поле заряженной сферы:

Поле равномерно заряженной сфериче­ской поверхности. Сферическая поверхность ра­диуса R с общим зарядом Q заряжена равно­мерно с поверхностной плотностью +0. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией.

Поэтому линии напря­женности направлены радиально. Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r > R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса, 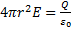, откуда: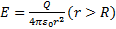

При r > R поле убывает с расстоянием по такому же закону, как у точечного заряда. Если r' < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0).

Дата добавления: 2015-04-24