Малая выборка. Практика применения малой выборки в коммерческой деятельности

Таблицы интеграла вероятностей используются для выборок большого объема из бесконечнобольшой генеральной совокупности. Но уже при п < \ 00 получается несоответствие междутабличными данными и вероятностью предела; при п < 100 погрешность становитсязначительной. Несоответствие вызывается главным образом характером распределения единицгенеральной совокупности. При большом объеме выборки особенность распределения вгенеральной совокупности не имеет значения, так как распределение отклонений выборочногопоказателя от генеральной характеристики при большой выборке всегда оказываетсянормальным.

В выборках небольшого объема п ≤ 30 характер распределения генеральной совокупностисказывается на распределении ошибок выборки. Поэтому для расчета ошибки выборки принебольшом объеме наблюдения (уже менее 100 единиц) отбор должен проводиться изсовокупности, имеющей нормальное распределение.

Теория малых выборок разработана английским статистиком В. Госсетом (писавшим подпсевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение,которое позволяет и при малых выборках соотносить t и доверительную вероятность F(t). При п> 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интегралавероятностей Лапласа, при 30 ≤ п ≤ 100 различия незначительны. Поэтому практически к малымвыборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка собъемом более 100 единиц).

Использование малых выборок в ряде случаев обусловлено характером обследуемойсовокупности. Так, в селекционной работе «чистого» опыта легче добиться на небольшом числеделянок. Производственный и экономический эксперимент, связанный с экономическимизатратами, также проводится на небольшом числе испытаний.

При контроле качества товаров в экономических исследованиях эксперимент может проводиться на основе малой выборки.

Под малой выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.
Средняя ошибка малой выборки 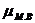вычисляется по формуле:
,
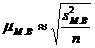где 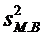— дисперсия малой выборки.
При определении дисперсии 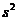число степеней свободы равно n-1:
.
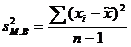Предельная ошибка малой выборки 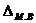определяется по формуле

При этом значение коэффициента доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, в которых даны распределения стандартизированных отклонений:
.

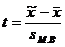5. Способы распространения характеристик выборки на генеральную совокупность.

Выборочный метод чаще всего применяется для получения характеристик генеральной совокупности по соответствующим показателям выборки. В зависимости от целей исследований это осуществляется или прямым пересчётом показателей выборки для генеральной совокупности, или посредством расчёта поправочных коэффициентов.

Способ прямого пересчёта. Он состоит в том, что показатели выборочной доли 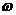или средней 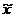распространяется на генеральную совокупность с учётом ошибки выборки.

Способ поправочных коэффициентов. Применяется в случаях, когда целью выборочного метода является уточнение результатов сплошного учета. Для этого после обобщения данных сплошного учета практикуется 10%-ное выборочное обследование с определением так называемого “процента недоучета”.

Так, например, если в хозяйствах населения поселка по данным 10%-ной выборки было зарегистрировано 52 головы скота, а по данным сплошного учета в этом массиве значится 50 голов, то коэффициент недоучета составляет 4% [(2*50):100]. С учетом полученного коэффициента вносится поправка в общую численность скота, находящегося у населения данного поселка.

47. Статистическая совокупность и статистический показатель, их роль и значение в экономико-статистических явлениях.

смотреть билет 2,4,56,57

Дата добавления: 2015-04-24