Геометрическая взвешенная

Геометрическая простая

Для расчетов средней геометрической простой используется формула:

где:

xi — цепной коэффициент роста

n — число этих коэффициентов роста

П — знак произведения

Для определения средней геометрической взвешенной применяется формула:

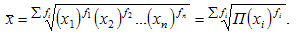
25. Средние позиционные: мода и медиана

Структурные средние занимают определенное место (или позицию) в вариационном ряду.

· Мода – это значение признака, наиболее часто встречающееся в исследуемой совокупности. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.

В дискретных вариац.рядах МОДА – знач-е варианты с наиб.частотой.

В интервальных вар.рядах определ-ся модальный интервал – интервал с наиб.частотой.

Мо – мода

Хо – нижняя граница мод.интервала

n – величина модального интервала

fm – частота модального интервала

fm-1 – частота интервала, предшествующего модальному

fm+1 – частота интервала, следующего за модальным.

· Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот, а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле: Ме = (n(число признаков в совокупности) + 1)/2, в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

где h – величина медианного интервала, х0 – нижняя граница интервала, кот.содержит медиану, Sm-1 – накопленная частота интервала, предшествующего медианам, fm - частота медианного интервала, 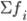- сумма частот или число членов ряда.

26. Средние позиционные: квартили и децили

Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.

Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Различают квартиль первого порядка (нижний квартиль – Q1) и квартиль третьего порядка (верхний квартиль – Q3). Каждый из них отсекает соответственно ¼ и ¾ совокупности. Средний квартиль делит сов-ть пополам и являя-ся медианой.

Q1 = XQ1 +i * (∑f/4 - SQ1-1)/fQ

Q3 = XQ3 + i * (3/4∑f - SQ3-1)/fQ3

Q1 = 300 + 50 * (125-60)/100 = 332,5

Для расчета первого квартиля находим ј всех частот: ∑f/4 составит 125 (500/4). Из таблицы 3 видно, что 125-я варианта находится в интервале 300 - 350.

Следовательно, XQ1 = 300. Сумма накопленных частот до этого интервала равна 60 (SQ1-1), частота этого интервала - 100. Расчет дает значение первого квартиля 332,5 тыс. руб. Это означает, что у трех четвертей всех рабочих заработная плата составляет 332,5 тыс. руб. и выше.

Рассчитаем третий квартиль. Три четверти численности частот (3/4 ∑f) составит 375 = 500*3/ 4. 375-я варианта находится в интервале 400 - 450. Следовательно:

Q3 = 400 + 50 *(375 - 275)/180 = 427,75

Третий квартиль составляет 427,75 тыс. руб. Следовательно, заработная плата каждого четвертого работника превышает 427,75 тыс. руб.

Децили – это значения признака в упорядоченной по возрастанию совокупности, которые делят совокупность на десять равных частей. Первая или нижняя дециль (D1) характеризует значение признака, меньше которого расположено 10% единиц совокупности, а больше – 90%. Девятая или верхняя дециль (D9) характеризует значение признака, меньше которого расположено 90% единиц совокупности, а больше – 10%.

Дата добавления: 2015-04-24